[CSP-S模拟测试]:蛇(DP+构造+哈希)
题目传送门(内部题140)
输入格式
前两行有两个长度相同的字符串,描述林先森花园上的字母。
第三行一个字符串$S$。
输出格式
输出一行一个整数,表示有多少种可能的蛇,对$10^9+7$取模。
样例
样例输入1:
rwby
ybwr
rwby
样例输出1:
4
样例输入2:
ooo
ooo
oo
样例输出2:
14
数据范围与提示
对于$20\%$的数据,$n,|S|\leqslant 16$。
对于$40\%$的数据,$n,|S|\leqslant 40$。
对于$60\%$的数据,$n,|S|\leqslant 200$。
对于$100\%$的数据,$1\leqslant n,|S|\leqslant 2,000$,输入中只包含小写字母。
题解
先来考虑路径蛇的路径,可以将其拆解成如下图中的三部分$\downarrow$
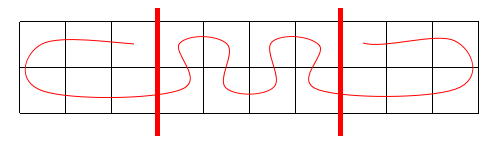
蛇一定是先向一个方向走$a$格,再回来;然后乱走(扭动着),然后再向另一个方向走$b$格,再回来。
一样不一样可以用哈希判断。
然后考虑$DP$,定义$dp[i]][j][k]$表示到了点$(i,j)$,匹配到了$k$的方案数。
避免出现环可以外层循环$k$。
为了方便,可以先默认向一个方向走;然后再把整张图翻转再跑一遍就好了。
注意蛇的长度为$1$和$2$的情况下需要特判。
时间复杂度:$\Theta(|S|^2)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
const int mod=1000000007;
struct rec{int s,x,y;};
int a[2][2001],b[2001],n,s;
char ch[2001];
long long dp[2][2001][4001][2],ans;
unsigned long long hsh[2001],flag[2001]={1},has[2][2][2002];
unsigned long long ask(bool x,bool y,int l,int r){return y?has[x][y][r]-has[x][y][l+1]*flag[l-r+1]:has[x][y][r]-has[x][y][l-1]*flag[r-l+1];}
unsigned long long get(int l,int r){return hsh[r]-hsh[l-1]*flag[r-l+1];}
void work()
{
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
has[i][0][j]=has[i][0][j-1]*131+a[i][j];
for(int i=0;i<2;i++)
for(int j=n;j;j--)
has[i][1][j]=has[i][1][j+1]*131+a[i][j];
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
{
dp[i][j][1][0]=(a[i][j]==b[1]);
for(int k=2;k<=j;k++)
dp[i][j][k<<1][1]=(ask(i^1,1,j,j-k+1)==get(1,k))&&(ask(i,0,j-k+1,j)==get(k+1,k<<1));
}
for(int k=1;k<=s;k++)
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
{
if(a[i][j]!=b[k])continue;
dp[i][j][k][0]=(dp[i][j][k][0]+dp[i][j-1][k-1][0]+dp[i][j-1][k-1][1])%mod;
dp[i][j][k][1]=(dp[i][j][k][1]+dp[i^1][j][k-1][0])%mod;
}
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
for(int k=0;k<=s;k++)
{
int res=(s-k)>>1;
if(!((s-k)&1)&&res!=1&&(s==k||(j+res<=n&&ask(i,0,j+1,j+res)==get(k+1,k+res)&&ask(i^1,1,j+res,j+1)==get(s-res+1,s))))
ans=(ans+dp[i][j][k][0]+dp[i][j][k][1])%mod;
}
}
int main()
{
scanf("%s",ch+1);n=strlen(ch+1);
for(int i=1;i<=n;i++)a[0][i]=ch[i]-'a'+1;
scanf("%s",ch+1);
for(int i=1;i<=n;i++)a[1][i]=ch[i]-'a'+1;
scanf("%s",ch+1);s=strlen(ch+1);
for(int i=1;i<=s;i++)
{
b[i]=ch[i]-'a'+1;
flag[i]=flag[i-1]*131;
hsh[i]=hsh[i-1]*131+b[i];
}
work();
reverse(a[0]+1,a[0]+n+1);
reverse(a[1]+1,a[1]+n+1);
memset(dp,0,sizeof(dp));
work();
if(s==1)
{
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
ans-=(a[i][j]==b[1]);
}
if(s==2)
{
for(int i=0;i<2;i++)
for(int j=1;j<=n;j++)
ans-=(a[i][j]==b[1]&&a[i^1][j]==b[2]);
}
printf("%lld",ans);
return 0;
}
rp++

