[CSP-S模拟测试]:最小值(DP+乱搞)
题目背景
$Maxtir$更喜欢序列的最小值。
题目传送门(内部题128)
输入格式
第一行输入一个正整数$n$和四个整数$A,B,C,D$。
第二行输入$n$个整数,第$i$个数表示$a_i$。
输出格式
输出一行一个整数$ans$表示答案。
样例
样例输入:
5 0 0 1 10
9 9 5 2 6
样例输出:
81
数据范围与提示
对于$10\%$的数据,满足$n\leqslant 100$
对于$20\%$的数据,满足$n\leqslant 1,000$
对于另外$20\%$的数据,满足$A=B=0,C\leqslant 0$
对于$100\%$的数据,满足$n\leqslant 2\times 10^5,\forall|f(a_i)|\leqslant 10^{13}$,输入数据均在整数$int$范围内
题解
第一眼,$\Theta(n^2)DP$,设$dp[i]$表示选到$i$的最大贡献。
转移很简单,枚举转移点即可。
第二眼,数据不好造,于是可以$j\geqslant \max(0,i-106)$就好啦……
其实我也不知道为什么$105$就$WA50$,$106$就直接$AC$了这也太巧了吧……
最后讲个故事,快搬好小板凳!!!
(话说你们为什么都爱听我讲故事额……
北岸大神:“动动,为什么我$QJ$还是会$TLE30$哇?!”
我:“???,不可能哇~“
北岸大神:”我调成$300$了!“
北岸大神:”我调成$100$了!“
北岸大神:”我$TM$都调成$1$了!!!“
我:”那你确定你写的是$j\geqslant \max(0,i-106)$嘛?“
北岸大神:”确定哇“
然而$\downarrow$
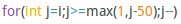
我:”……“
北岸大神:”窝槽“
左拐头朝下,小心别挂树叉上,忒疼。
时间复杂度:$\Theta(106\times n)$。
期望得分:$10$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int n,A,B,C,D;
long long a[200001];
long long dp[200001];
int main()
{
memset(dp,-0x3f,sizeof(dp));
scanf("%d%d%d%d%d",&n,&A,&B,&C,&D);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
dp[0]=0;
for(int i=1;i<=n;i++)
{
int minn=max(0,i-106);
long long res=a[i];
for(int j=i-1;j>=minn;j--)
{
dp[i]=max(dp[i],dp[j]+A*res*res*res+B*res*res+C*res+D);
res=min(res,a[j]);
}
}
printf("%lld",dp[n]);
return 0;
}
rp++


