[CSP-S模拟测试]:二叉搜索树(DP+贪心)
题目传送门(内部题99)
输入格式
第一行一个整数$n$,第二行$n$个整数$x_1\sim x_n$。
输出格式
一行一个整数表示答案。
样例
样例输入:
5
8 2 1 4 3
样例输出:
35
数据范围与提示
样例解释:
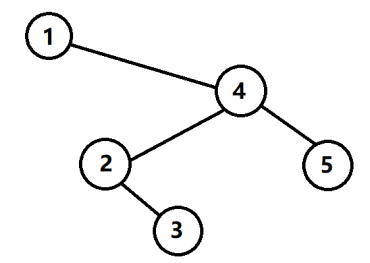
数据范围:
对于$10\%$的数据,$n\leqslant 10$。
对于$40\%$的数据,$n\leqslant 300$。
对于$70\%$的数据,$n\leqslant 2,000$。
对于$100\%$的数据,$n\leqslant 5,000,1\leqslant x_i\leqslant 10^9$。
提示:
二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;它的左、右子树也分别为二叉搜索树。
题解
因为满足二叉搜索树的性质,所以一棵子树里的点一定是连续的。
考虑$DP$,不妨一步一步来考虑,设$dp[x][l][r]$表示区间$[l,r]$的跟节点深度为$x$的最小代价。
转移很简单,无非就是枚举$[l,r]$中哪个点做跟节点即可,时间复杂度是$\Theta(n^4)$的。
(考虑一个小优化:因为深度其实远远达不到$n$,也就是$\log n$多一点,所以直接扫到$10$左右就能拿到$40$分啦~)
考虑优化,发现深度每增加$1$,也就相当于又加了一个$\sum \limits_{i=l}^r x_i$,用前缀和优化就有了$\Theta(n^3)$的做法了。
接着优化,考虑贪心,因为决策点一定是单调的,做个解释,假设现在要处理区间$[l,r]$,在处理它之前我们已经处理出来了$[l,r-1]$和$[l+1,r]$,并且知道了它们的最优决策点,那么$[l,r]$的最优决策点一定在$[l,r-1]$和$[l+1,r]$的最优决策点之间。
时间复杂度:$\Theta(n^2)$(均摊)。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int n;
long long v[5001],s[5001];
pair<long long,int> dp[5001][5001];
int main()
{
memset(dp,0x3f,sizeof(dp));
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&v[i]);
s[i]=s[i-1]+v[i];
dp[i][i]=make_pair(v[i],i);
}
for(int i=2;i<=n;i++)
{
for(int l=1;l<=n-i+1;l++)
{
int r=l+i-1;
for(int mid=dp[l][r-1].second;mid<=dp[l+1][r].second;mid++)
{
long long res=s[r]-s[l-1];
if(l<=mid-1)res+=dp[l][mid-1].first;
if(mid+1<=r)res+=dp[mid+1][r].first;
if(res<dp[l][r].first)dp[l][r]=make_pair(res,mid);
}
}
}
printf("%lld",dp[1][n]);
return 0;
}
rp++


