[CSP-S模拟测试]:邻面合并(状压DP)
题目背景
$NEWorld$作为一个$3D$游戏,对渲染(图形绘制)的效率要求极高。当玩家扩大视野范围时,可见的方块面数量将会迅速增多,以至于大量的顶点处理很快就成为了图形管线中的瓶颈。乔猫想了想,决定在大量绘制前,预处理一些相邻且有着相同材质的方块面——将许多小的面合成一个大的面,便可以在不改变渲染结果的同时减少很多顶点数量了吧......
题目描述
给定一个$N\times M$的网格,每个格子上写有$0$或$1$。现在用一些长方形覆盖其中写有$1$的格子,长方形的每条边都要与坐标轴平行。要求:每个写着$1$的格子都要被覆盖,长方形不可以重叠(重复绘制也多少会增加性能开销),也不能覆盖到任何一个写着$0$的格子(不然绘制结果就不正确了)。请问最少需要多少长方形?
输入格式
输入文件名为$merging.in$。
输入文件第一行两个正整数$N,M$,表示网格大小为$N$行$M$列。
接下来的$N$行,每行$M$个正整数$A_{ij}$(保证均为$0$或$1$),其中第$i$行$j$列的正整数表示网格$i$行$j$列里填的数。
样例
样例输入:
4 4
1 1 1 0
1 1 1 1
0 0 1 1
0 0 1 1
样例输出:
3
数据范围与提示
样例解释:
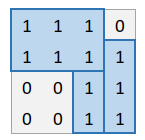
一种可行的覆盖方案(粗线表示分割线):
对于$30\%$的数据:$N,M\leqslant 5$。
对于$100\%$的数据:$N\leqslant 100,M\leqslant 8$。
数据范围:
对于$30\%$的数据:$N,M\leqslant 5$。
对于$100\%$的数据:$N\leqslant 100,M\leqslant 8$。
题解
观察$M$的范围,可以看出来应该是一个状压(当也有可能是轮廓线$DP$,甚至是插头$DP$)。
采用$8$进制压位表示每一位为起点的连续段的终点是几即可。
注意如果终点是$1$,那么起点也一定是$1$即可。
时间复杂度:$\THeta(N\times M\times 2^M)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int N,M;
int A[102][9];
bool vis[9][9];
int dp[102][150000];
vector<int> vec[102];
int ans=0x3f3f3f3f;
void dfs(int x,int y,int pre,int state)
{
if(y>M){if(!pre)vec[x].push_back(state);return;}
if(A[x][y])
{
if(!pre)
{
dfs(x,y+1,1,state|(1<<((y-1)<<1)));
dfs(x,y+1,0,state|(3<<((y-1)<<1)));
}
else
{
dfs(x,y+1,1,state);
dfs(x,y+1,0,state|(2<<((y-1)<<1)));
}
}
else
{
if(pre)return;
else dfs(x,y+1,0,state);
}
}
int main()
{
memset(dp,0x3f,sizeof(dp));
scanf("%d%d",&N,&M);
for(int i=1;i<=N;i++)
for(int j=1;j<=M;j++)
scanf("%d",&A[i][j]);
for(int i=1;i<=N;i++)dfs(i,1,0,0);
for(int j=0;j<vec[1].size();j++)
{
int state=vec[1][j],res=0;
for(int i=1;i<=M;i++)
{
int flag=(state^(state>>(i<<1)<<(i<<1)))>>((i-1)<<1);
if(flag==1||flag==3)res++;
}
dp[1][state]=res;
}
for(int i=1;i<=N;i++)
{
for(int j=0;j<vec[i].size();j++)
{
int state=vec[i][j];
memset(vis,0,sizeof(vis));
for(int k=1,l;k<=M;k++)
{
switch((state^(state>>(k<<1)<<(k<<1)))>>((k-1)<<1))
{
case 1:l=k;break;
case 2:vis[l][k]=1;break;
case 3:vis[k][k]=1;break;
}
}
for(int k=0;k<vec[i+1].size();k++)
{
int staet=vec[i+1][k],res=0;
for(int l=1,h;l<=M;l++)
{
switch((staet^(staet>>(l<<1)<<(l<<1)))>>((l-1)<<1))
{
case 1:h=l;break;
case 2:res+=!vis[h][l];break;
case 3:res+=!vis[l][l];break;
}
}
dp[i+1][staet]=min(dp[i+1][staet],dp[i][state]+res);
}
}
}
for(int i=0;i<vec[N].size();i++)ans=min(ans,dp[N][vec[N][i]]);
printf("%d",ans);
return 0;
}
rp++


