[CSP-S模拟测试]:小P的2048(模拟)
题目描述
最近,小$P$迷上了一款叫做$2048$的游戏。这块游戏在一个$n\times n$的棋盘中进行,棋盘的每个格子中可能有一个形如$2^k(k\in N^*)$的数,也可能是空的。游戏规则介绍如下:
$1.$游戏开始时棋盘内将会生成两个数字,生成的数字仅可能为$2$或$4$;
$2.$每次操作,玩家可以选择上、下、左、右四个方向进行平移;
$3.$以向上平移为例,从上往下考虑每个不为空的格子,若上方与之相邻的格子为空,则将该格子上的数字移动至相邻格子。在一次位移中,每个数字会进行多次移动直到不能移动为止。
$4.$以向上平移为例,从上往下考虑每个不为空的格子,若上方与之相邻的数字恰好与其相等,则两个数字可以合并,新生成的数字为原来两个数之和。在一次合并中,每个数字只能与其它数合并一次,可以同时合并多对数字,但不能连续合并;
$5.$每次操作由位移+合并+位移组成,若操作后棋盘局面发生变化,则该操作为有效操作,其有效得分为合并过程中所有新生成的数字之和;
$6.$在每次操作后,棋盘内都会新生成一个数字$2$或$4$,数字只会在空格子处生成;
$7.$当棋盘被数字填满,玩家无法进行任何有效操作时,游戏结束,游戏总得分为所有操作的有效得分之和。
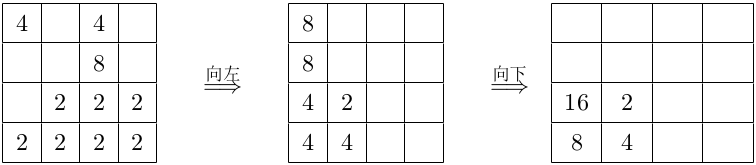
为了降低难度,小$P$对$2048$游戏进行了一些改动。在游戏开始前,小$P$会告诉你棋盘的初始状态,并给你若干次操作。每次操作由方向变量、位置参数和一个数字组成,方向变量代表你在本次操作中的移动方向,给定的数字为本次操作之后将会生成的数字的大小,而位置参数将决定生成数字的位置。若位置参数为$K$,操作后棋盘中空格子的数量为$r$,则生成数字的位置从上到下、从左到右第$(1+K\mod r)$个空格子。如果每次操作为无效操作,则游戏结束,而当所有操作都完成后,游戏同样结束。(注意:改动后,游戏结束时棋盘不一定被数字填满。)

现在小$P$问你,在游戏结束前你一共进行了多少次有效操作,最后你的游戏总得分是多少。
输入格式
第一行为两个正整数$n$和$m$,分别表示棋盘的大小和操作的个数。
第二行为六个正整数$x_1,y_1,v_1$和$x_2,y_2,v_2$($x_1,y_1,x_2,y_2\leqslant n,v_1,v_2\in\{2,4\}$),分别代表游戏开始时,棋盘上两个数字的位置(行/列)的大小。行号从上往下的编号,列号从左往右的编号,编号均以$1$开始。
接下来$m$行,表示小$P$给你的$m$个操作。每行由三个自然数$D_i,K_i,V_i$组成,其中$D_i$代表本次操作的平移方向,$0/1/2/3$分别代表上/下/左/右。$K_i$为位置参数,$V_i$为操作后生成的数的大小。($D_i\in\{0,1,2,3\},K_i<2^{31},V_i\in\{2,4\}$)
输出格式
输出共两行,每行一个正证书,分别代表你完成的有效操作数与游戏总得分。
样例
样例输入:
3 6
2 1 2 3 2 4
1 14 2
1 6 4
2 10 2
0 3 2
2 17 2
3 14 4
样例输出:
4
12
数据范围与提示
样例解释:

四次有效操作后,棋盘无法继续向左平移,故游戏结束,总得分为$4+8=12$。
数据范围:
对于$10\%$的数据:$n=2$
对于$40\%$的数据:$n\leqslant 4,m\leqslant 100$
对于$100\%$的数据:$2\leqslant n\leqslant 8,1\leqslant m\leqslant 100000$
题解
大模拟,注意以下几点:
$\alpha.$输出格式。
$\beta.$大样例中没有向右的操作,所以要特别注意向右(考试时因为这个挂到飞起……)
$\gamma.$数组勤清空。
$\delta.$有数据点一开始的两个坐标是一个,所以避免使用记录空格子的个数的方法。
时间复杂度:$\Theta(n^2m)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int n,m,x,y,v,x2,y2,v2;
int Map[10][10];
long long ans;
int que[10];
bool up(int k,int v)
{
bool res=0;
int r=0;
for(int i=1;i<=n;i++)
{
memset(que,0,sizeof(que));
for(int j=1;j<=n;j++)
if(Map[j][i])
{
if(j>1&&!Map[j-1][i])res=1;
que[++que[0]]=Map[j][i];
}
for(int j=1;j<=n;j++)
Map[j][i]=que[j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(Map[j][i]==Map[j+1][i]&&Map[j][i])
{
res=1;
Map[j][i]<<=1;
Map[j+1][i]=0;
ans+=Map[j][i];
}
for(int i=1;i<=n;i++)
{
memset(que,0,sizeof(que));
for(int j=1;j<=n;j++)
if(Map[j][i])
{
if(j>1&&!Map[j-1][i])res=1;
que[++que[0]]=Map[j][i];
}
for(int j=1;j<=n;j++)
Map[j][i]=que[j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!Map[i][j])r++;
if(!r)return 0;
r=1+k%r;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!Map[i][j])
{
r--;
if(!r){Map[i][j]=v;goto nxt;}
}
nxt:return res;
}
bool down(int k,int v)
{
bool res=0;
int r=0;
for(int i=1;i<=n;i++)
{
memset(que,0,sizeof(que));
for(int j=n;j;j--)
if(Map[j][i])
{
if(j<n&&!Map[j+1][i])res=1;
que[++que[0]]=Map[j][i];
}
int now=que[0];
reverse(que+1,que+que[0]+1);
for(int j=n;j;j--)
{
if(now)Map[j][i]=que[now--];
else Map[j][i]=0;
}
}
for(int i=1;i<=n;i++)
for(int j=n;j;j--)
if(Map[j][i]==Map[j-1][i]&&Map[j][i])
{
res=1;
Map[j][i]<<=1;
Map[j-1][i]=0;
ans+=Map[j][i];
}
for(int i=1;i<=n;i++)
{
memset(que,0,sizeof(que));
for(int j=n;j;j--)
if(Map[j][i])
{
if(j<n&&!Map[j+1][i])res=1;
que[++que[0]]=Map[j][i];
}
int now=que[0];
reverse(que+1,que+que[0]+1);
for(int j=n;j;j--)
{
if(now)Map[j][i]=que[now--];
else Map[j][i]=0;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!Map[i][j])r++;
if(!r)return 0;
r=1+k%r;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!Map[i][j])
{
r--;
if(!r){Map[i][j]=v;goto nxt;}
}
nxt:return res;
}
bool left(int k,int v)
{
bool res=0;
int r=0;
for(int i=1;i<=n;i++)
{
memset(que,0,sizeof(que));
for(int j=1;j<=n;j++)
if(Map[i][j])
{
if(j>1&&!Map[i][j-1])res=1;
que[++que[0]]=Map[i][j];
}
for(int j=1;j<=n;j++)
Map[i][j]=que[j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(Map[i][j]==Map[i][j+1]&&Map[i][j])
{
res=1;
Map[i][j]<<=1;
Map[i][j+1]=0;
ans+=Map[i][j];
}
for(int i=1;i<=n;i++)
{
memset(que,0,sizeof(que));
for(int j=1;j<=n;j++)
if(Map[i][j])
{
if(j>1&&!Map[i][j-1])res=1;
que[++que[0]]=Map[i][j];
}
for(int j=1;j<=n;j++)
Map[i][j]=que[j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!Map[i][j])r++;
if(!r)return 0;
r=1+k%r;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!Map[i][j])
{
r--;
if(!r){Map[i][j]=v;goto nxt;}
}
nxt:return res;
}
bool right(int k,int v)
{
bool res=0;
int r=0;
for(int i=1;i<=n;i++)
{
memset(que,0,sizeof(que));
for(int j=n;j;j--)
if(Map[i][j])
{
if(j<n&&!Map[i][j+1])res=1;
que[++que[0]]=Map[i][j];
}
int now=que[0];
reverse(que+1,que+que[0]+1);
for(int j=n;j;j--)
{
if(now)Map[i][j]=que[now--];
else Map[i][j]=0;
}
}
for(int i=1;i<=n;i++)
for(int j=n;j;j--)
if(Map[i][j]==Map[i][j-1]&&Map[i][j])
{
res=1;
Map[i][j]<<=1;
Map[i][j-1]=0;
ans+=Map[i][j];
}
for(int i=1;i<=n;i++)
{
memset(que,0,sizeof(que));
for(int j=n;j;j--)
if(Map[i][j])
{
if(j<n&&!Map[i][j+1])res=1;
que[++que[0]]=Map[i][j];
}
int now=que[0];
reverse(que+1,que+que[0]+1);
for(int j=n;j;j--)
{
if(now)Map[i][j]=que[now--];
else Map[i][j]=0;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!Map[i][j])r++;
if(!r)return 0;
r=1+k%r;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!Map[i][j])
{
r--;
if(!r){Map[i][j]=v;goto nxt;}
}
nxt:return res;
}
int main()
{
scanf("%d%d%d%d%d%d%d%d",&n,&m,&x,&y,&v,&x2,&y2,&v2);
Map[x][y]=v;Map[x2][y2]=v2;
for(int i=1;i<=m;i++)
{
int d,k,v;
scanf("%d%d%d",&d,&k,&v);
if(d==0)if(!up(k,v)){printf("%d\n%lld\n",i-1,ans);return 0;}
if(d==1)if(!down(k,v)){printf("%d\n%lld\n",i-1,ans);return 0;}
if(d==2)if(!left(k,v)){printf("%d\n%lld\n",i-1,ans);return 0;}
if(d==3)if(!right(k,v)){printf("%d\n%lld\n",i-1,ans);return 0;}
}
printf("%d\n%lld\n",m,ans);
return 0;
}
rp++

