[CSP-S模拟测试]:幻魔皇(数学)
题目描述
幻魔皇拉比艾尔很喜欢斐波那契树,他想找到神奇的节点对。
所谓斐波那契树,根是一个白色节点,每个白色节点都有一个黑色节点儿子,而每个黑色节点则有一个白色和一个黑色节点儿子。神奇的节点对则是指白色节点对。
请问对于深度为$n$的斐波那契树,其中距离为$i$的神奇节点对有多少个?拉比艾尔需要你对于$1\leqslant i\leqslant 2n$的所有$i$都求出答案。
输入格式
一行一个正整数$n$。
输出格式
一行$2n$个整数表示答案,对$123456789$取模。
样例
样例输入:
5
样例输出:
0 2 3 3 1 1 1 0 0 0 0
数据范围与提示
对于$20\%$的数据$n\leqslant 10$;
对于$40\%$的数据$n\leqslant 20$;
对于$60\%$的数据$n\leqslant 30$;
对于$80\%$的数据$n\leqslant 400$;
对于$100\%$的数据$n\leqslant 5,000$。
题解
先来看一下这棵树:
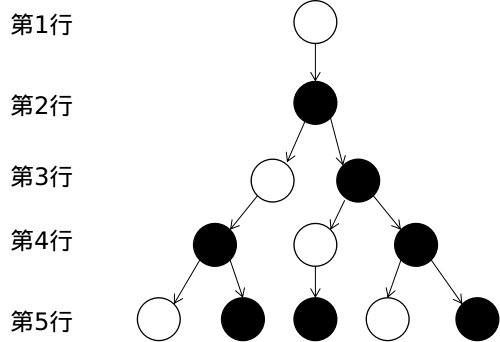
首先,来看几点性质:
$\alpha.$每一行的点数呈斐波那契数列。
$\beta.$从第二行开始,每行的黑点个数呈斐波那契数列。
$\gamma.$从第三行开始,每行的白点个数呈斐波那契数列。
$\delta.$对于每一个黑(白)点,如果它有一棵深度为$k$的子树,那么所有这些子树都是一样的。
得到了这些性质,再来看这道题:
设$w[i]$表示第$i$行的白点的个数,$b[i]$表示第$i$行黑点的个数,$sw[i]$表示小于等于$i$行的所有白点的个数,$sb[i]$表示小于等于$i$行的所有黑点的个数(注意此处的行数其实也是深度,根节点的深度为$1$)。
思考如何计数,根据性质$\delta$,可以考虑将每一棵不同的子树内部贡献,再乘上这样子树的数量即可得到答案。
再来考虑如何统计子树内部的贡献,可以大致分为两种情况:
$\alpha.$神奇节点对的$LCA$为白色点。
$\beta.$神奇节点对的$LCA$为黑色点。
观察上面的图可知,对于情况$\alpha$,$LCA$一定是其中一个白点,就是说这两个白点一定是祖先和后代的关系。
那么,对于一个深度为$k$的子树,其贡献为$w[i+1]$(因为祖先白点的行数是$1$),而这样的子树有$sw[n-i]$棵。
所以,对于情况$\alpha$,其对答案的贡献即为:
$$\sum \limits_{i=1}^n sw[n-i]\times w[i+1]$$
对于情况$\beta$,就显得麻烦很多了,两个白点必须在这个黑点($LCA$)的两个子节点的子树中。
考虑枚举两侧的距这个黑点的距离$i,j$(白色子节点的子树中的白点的距离为$i$,黑色子节点的子树中的白点的距离为$j$),并将这棵树进行如下图所示划分:
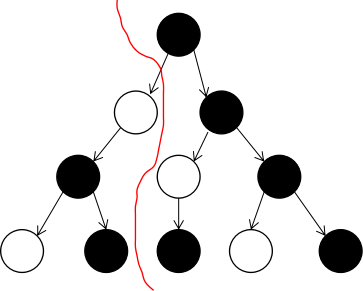
惊喜的发现,如果将右侧树的根节点由黑变白对答案没有影响,而右侧树就变成了一棵深度为$j+1$的普通树,那么其距离为$j$的白点就有$w[j+1]$个。
左侧深度为$i+1$,则对于左侧树其深度为$i$,所以距离为$i$的白点个数为$w[i]$。
那么对于这棵树,其对答案的贡献就是$w[i]\times w[j+1]$,而这样的子树的数量取决与$i,j$中更大的那一个,所以这样的子树有$sb[n-\max(i,j)]$棵。
所以,对于情况$\beta$,其对答案的贡献即为:
$$\sum \limits_{i=1}^n \sum \limits_{j=1}^n sb[n-\max(i,j)]\times w[i]\times w[j+1]$$
时间复杂度:$\Theta(n^2)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
const int mod=123456789;
int n;
long long w[5001],b[5001],sw[5001],sb[5001];
long long ans[10001];
int main()
{
scanf("%d",&n);
w[1]=w[3]=1;
sw[1]=sw[2]=1;sw[3]=2;
for(int i=4;i<=n;i++)
{
w[i]=(w[i-1]+w[i-2])%mod;
sw[i]=(sw[i-1]+w[i])%mod;
}
b[2]=1;sb[2]=1;
for(int i=3;i<=n;i++)
{
b[i]=(b[i-1]+b[i-2])%mod;
sb[i]=(sb[i-1]+b[i])%mod;
}
for(int i=1;i<=n;i++)
ans[i]=sw[n-i]*w[i+1]%mod;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
ans[i+j]=(ans[i+j]+sb[n-max(i,j)]*w[i]%mod*w[j+1])%mod;
for(int i=1;i<=2*n;i++)printf("%lld ",ans[i]);
return 0;
}
rp++

