[CSP-S模拟测试]:building(模拟)
题目传送门(内部题64)
输入格式
第一行有一个整数$id$,表示测试点编号。第二行有四个整数$n,m,k,q$。
然后有$k$行,每一行有四个整数$x_{i_1},y_{i_1},x_{i_2},y_{i_2}$。然后有$q$行,每一行有两个整数$u_i,v_i$。
输出格式
有$q$行,每一行一个整数表示答案。
样例
样例输入:
1
5 5 6 10
1 1 1 2
3 2 3 4
5 2 5 5
2 1 3 1
1 4 2 4
4 5 4 5
0 1
0 2
0 3
0 4
0 5
1 1
1 2
1 3
1 4
1 5
样例输出:
3
5
9
11
16
2
2
1
2
1
数据范围与提示
对于所有数据,$1\leqslant id\leqslant 20$,$n,m,k\leqslant 10^5$,$q\leqslant 2n$,$1\leqslant x_{i_1}\leqslant x_{i_2}\leqslant n$,$1\leqslant y_{i_1}\leqslant y_{i_2}\leqslant m$,$u_i\in\{0,1\}$,$v_i\leqslant n$。
题解
又没有打正解,是因为没看懂题解(我太菜辣)。
我们先来考虑$u=0$的情况,也就是我们只需要求出楼盘总数。
可以用前缀和轻松解决。
那么再来考虑$u=1$的情况,不重叠这个性质超级棒!
先只考虑$x_{i_1}=x_{i_2}$的情况,我们将其按$x$为第一维排序,$y$为第二维排序,然后首先判断其与前面一个有没有联通,在判断其与上一行有没有联通,大致可以分为以下四种情况$\downarrow$

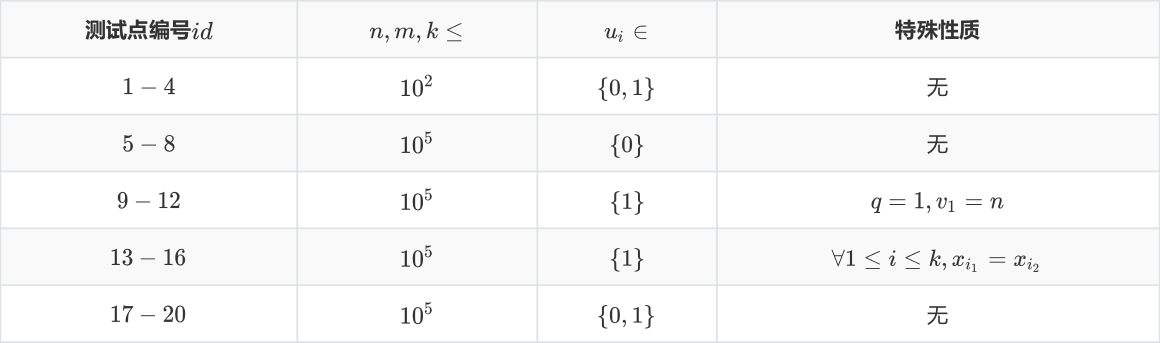
你可能觉得,如果有两个相邻,我就将块数$--$,但是这样是错的,比如下图中的情况$\downarrow$

然后你就去世了……
因为我们在考虑最下面的$4$的时候发现它与$2$和$3$都相邻,但是$2$与$3$都与$1$联通,考虑的时候就已经在一个联通块里了。
不用担心,并查集维护一下就好啦~
下面在来考虑一般情况,为方便,忽略一些可以可以归为一类的情况,将其大致分为一下四种情况$\downarrow$

第一种情况上面已经讨论了,下面来看其它情况。
我们可以开两个$vector$,分别记录每一行和每一列有哪个矩形的$(x_{i_2},y_{i_2})$,因为本题保证了没有重叠,所以只用记录$(x_{i_2},y_{i_2})$,处理每一个矩行的时候暴力扫一遍上一行的$vector$和相邻列的$vector$,为什么需要扫相邻两列的$vector$而不是只扫左边这一列的,因为会出现下面这种情况$\downarrow$
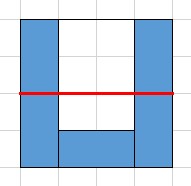
我们在扫到红线这一行的时候还没有扫到最下面的矩形,所以两侧的矩形还不能合并到一起,而我们在扫到最下面一行的矩形的时候才需要合并两侧的矩形。
而对于行,我们则不用考虑这个问题,这就是上面行只用扫上面一行,而列则要扫相邻两列的原因。
有了这些,就是疯狂的调代码了,建议现将$\forall1\leqslant i\leqslant k,x_{i_1}=x_{i_2}$的部分分拿到再冲击正解,因为这个部分分的思想很重要。
虽说我的算法会被极限数据卡成$\Theta(n^2)$,但是随机数据基本上是线性的。
时间复杂度:$\Theta($玄学$)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct rec{int x0,x2,y0,y2;}e[100001];
int id,n,m,k,q,u,v;
int fa[100001];
long long s1[100001],s2[100001];
vector<int> vec[100002],vet[100002];
bool cmp(rec a,rec b){return a.x0==b.x0?a.y0<b.y0:a.x0<b.x0;}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
int main()
{
scanf("%d%d%d%d%d",&id,&n,&m,&k,&q);
for(int i=1;i<=k;i++)
scanf("%d%d%d%d",&e[i].x0,&e[i].y0,&e[i].x2,&e[i].y2);
sort(e+1,e+k+1,cmp);
for(int i=1;i<=k;i++)
{
vec[e[i].y2].push_back(i);
vet[e[i].x2].push_back(i);
fa[i]=i;
}
long long sum=0;
for(int i=1;i<=k;i++)
{
if(e[i].x0==e[i].x2){s1[e[i].x0]+=e[i].y2-e[i].y0+1;s1[e[i].x0+1]-=e[i].y2-e[i].y0+1;}
else{s1[e[i].x0]++;s1[e[i].x2+1]--;}
if(e[i].x0!=e[i-1].x0)for(int j=e[i-1].x0;j<e[i].x0;j++)s2[j]=sum;
sum++;
for(int j=0;j<vet[e[i].x0-1].size();j++)
{
int x=find(i);
int y=find(vet[e[i].x0-1][j]);
if(x==y)continue;
if((e[vet[e[i].x0-1][j]].y0<=e[i].y0&&e[i].y0<=e[vet[e[i].x0-1][j]].y2)||(e[i].y0<=e[vet[e[i].x0-1][j]].y0&&e[vet[e[i].x0-1][j]].y0<=e[i].y2))
{
sum--;
fa[x]=y;
}
}
for(int j=0;j<vec[e[i].y0-1].size();j++)
{
if(e[vec[e[i].y0-1][j]].x0>e[i].x0)continue;
int x=find(i);
int y=find(vec[e[i].y0-1][j]);
if(x==y)continue;
if((e[vec[e[i].y0-1][j]].x0<=e[i].x0&&e[i].x0<=e[vec[e[i].y0-1][j]].x2)||(e[i].x0<=e[vec[e[i].y0-1][j]].x0&&e[vec[e[i].y0-1][j]].x0<=e[i].x2))
{
sum--;
fa[x]=y;
}
}
for(int j=0;j<vec[e[i].y2+1].size();j++)
{
if(e[vec[e[i].y2+1][j]].x0>e[i].x0)continue;
int x=find(i);
int y=find(vec[e[i].y2+1][j]);
if(x==y)continue;
if((e[vec[e[i].y2+1][j]].x0<=e[i].x0&&e[i].x0<=e[vec[e[i].y2+1][j]].x2)||(e[i].x0<=e[vec[e[i].y2+1][j]].x0&&e[vec[e[i].y2+1][j]].x0<=e[i].x2))
{
sum--;
fa[x]=y;
}
}
}
for(int i=e[k].x0;i<=n;i++)s2[i]=sum;
for(int i=1;i<=n;i++)s1[i]+=s1[i-1];
for(int i=1;i<=n;i++)s1[i]+=s1[i-1];
while(q--)
{
scanf("%d%d",&u,&v);
if(u)printf("%lld\n",s2[v]);
else printf("%lld\n",s1[v]);
}
return 0;
}
rp++

