[CSP-S模拟测试]:砖块（模拟）
题目描述
在一个二维网格平面上，一个网格的坐标由其左下角的点的坐标定义$(x,y)$。在一个二维网格平面上，一个网格的坐标由其左下角的个点的坐标定义$(0,0)$的区域中，此时存在高度为$k$的初始砖块，$k\in [1,10]$。然后，在一系列动作中，砖块会滚动到棋盘上的其他位置。一步是将砖块相对于当前板上的墙的四个边缘之一旋转$90°$的角度。作为移动的结果，砖块改变其在平面上的位置，使得它可以沿另一个面继续旋转。砖块的变换的四个可能的方向用字母$N,S,W,E$标记。
在下图中，有一个高度为$2$的砖，它在初始位置。箭头表示可以由块制作的四种运动。
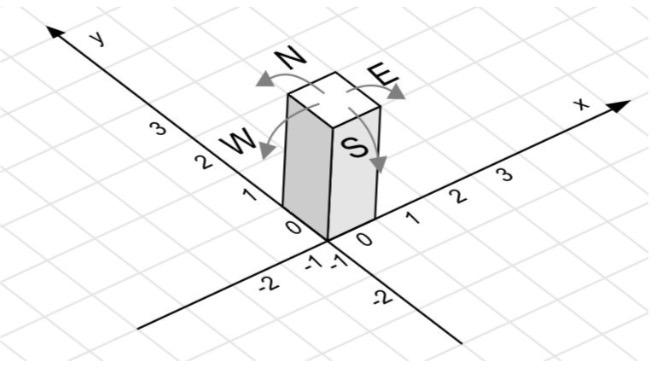
在随后的运动中，块被滚动到棋盘的下一个位置，以便其随后的面与地面接触。下图显示了块的移动示例。
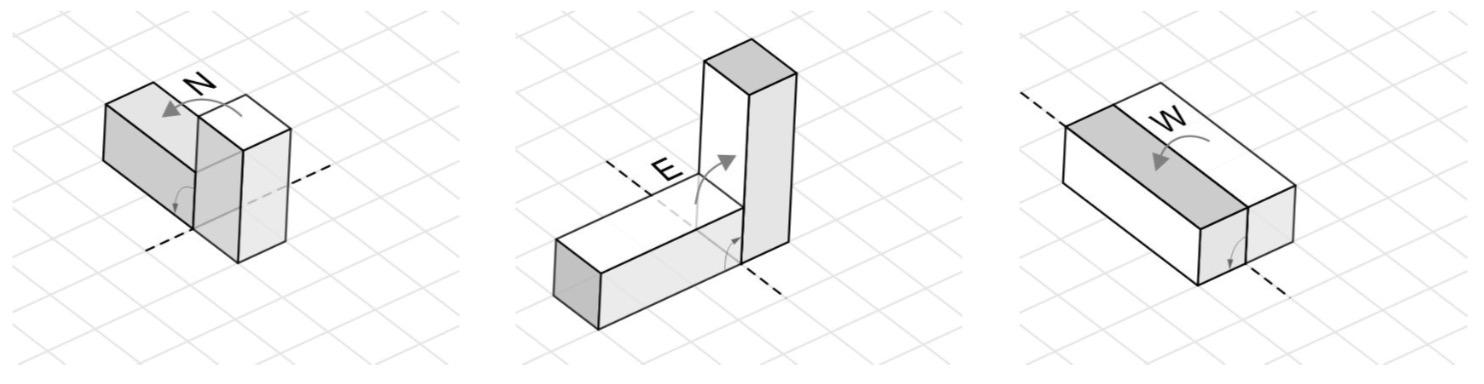可以发现，每一步之后都会有若干个网格被覆盖。你的任务是这样的，给定高度$k$和操作序列，求出最终被覆盖的网格的坐标以及所有网格中被覆盖次数最多的网格的被覆盖次数。
注:初始位置算被覆盖一次。
输入格式
第一行整数$N$，表示测试组数。
一组测试数据的输入数据放在两行中。
在第一行中有一个从$1$到$10$的数字，用于定义块在初始位置的高度。
第二行包含长度为$1$到$100$个字符的文本字符串。这些字符是字母$N,S,W,E$，定义了滚动块的四个可能方向。$"N"$表示朝向$y$轴正向翻滚，$"S"$朝向负向$y$轴返回滚动该块。$"E"$表示朝向正$x$轴旋转滚动块，而朝相反方向滚动块$"W"$。
输出格式
输出中，每组测试数据输出三行。
第一行，砖块的最后覆盖位置的$x$坐标，按照从小到大的顺序列出。
第二行，砖块在最终覆盖位置的$y$坐标，按照从小到大的顺序列出。
第三行，输出所有网格中被覆盖次数最多的网格的被覆盖次数。
样例
样例输入：
3
2
ENEESESSESWWWN
5
WNSEWNSEWNSEWWSEN
3
NNEEESESWWNWWWWWSSEEEEENNE
样例输出：
3 3
-3 -2
1-5
0
8
7 8 9
5 5 5
3
数据范围与提示
样例解释：
测试$1$：在$14$个动作中，一个高度为$2$的砖被滚动，在任何区域都没有被覆盖超过一次。完成所有动作后，该块将位于字段$(3,-3)(3,-2)$中。
测试$2$：在$17$次移动中，一个高度为$5$的块被滚动。在其路线中，最多$8$次覆盖了同一网格中。完成所有动作后，该块将被放置在场上$(-5,0)$。
测试$3$：在$26$个动作中，一个高度为$3$的砖被滚动。完成所有动作后，垫将会在场$(7,5)(8,5)(9,5)$中。
数据范围：
对于$40\%$的数据，$k=1$
对于$100\%$的数据，$k\in [1,10],N\in [1,100]$。操作长度$\leqslant 100$
题解
其实就是一道模拟送分题，一堆的$if\ else$就好了。
简单说一下我的做法，我只记录长方体左下角的位置坐标（因为会有负，所以要注意，可以加一个$base$）和现在的状态（分为立着，纵向躺，横向躺），剩下的就看模拟功底了，一般人大约需要$40$分钟。
需要特别注意的一点就是清空问题，千万不要$memset$，或者把数组开小一点，因为最多只会朝一个方向走$550$格（为那些开$5000\times 5000$的人默哀……）。
时间复杂度：$\Theta(N\times k\times |S|)$。
期望得分：$100$分。
实际得分：$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
const int base=570;
int x,y,k,n,now;
char ch[101];
int Map[1151][1151];
int minx,maxx,miny,maxy;
void pre_work()
{
minx=miny=0x3f;
maxx=maxy=0;
x=y=base;
now=0;
}
void N()
{
switch(now)
{
case 0:
for(int i=y+1;i<=y+k;i++)
Map[x][i]++;
y++;
now=1;
return;
case 1:
y+=k;
Map[x][y]++;
now=0;
return;
case 2:
y++;
for(int i=x;i<x+k;i++)
Map[i][y]++;
return;
}
}
void S()
{
switch(now)
{
case 0:
for(int i=y-1;i>=y-k;i--)
Map[x][i]++;
y-=k;
now=1;
return;
case 1:
y--;
Map[x][y]++;
now=0;
return;
case 2:
y--;
for(int i=x;i<x+k;i++)
Map[i][y]++;
return;
}
}
void W()
{
switch(now)
{
case 0:
for(int i=x-k;i<x;i++)
Map[i][y]++;
x-=k;
now=2;
return;
case 1:
x--;
for(int i=y;i<y+k;i++)
Map[x][i]++;
return;
case 2:
x--;
Map[x][y]++;
now=0;
return;
}
}
void E()
{
switch(now)
{
case 0:
for(int i=x+1;i<=x+k;i++)
Map[i][y]++;
x++;
now=2;
return;
case 1:
x++;
for(int i=y;i<y+k;i++)
Map[x][i]++;
return;
case 2:
x+=k;
Map[x][y]++;
now=0;
return;
}
}
void getxy()
{
switch(now)
{
case 0:
printf("%d\n%d\n",x-base,y-base);
return;
case 1:
for(int i=1;i<=k;i++)printf("%d ",x-base);
puts("");
for(int i=y;i<y+k;i++)printf("%d ",i-base);
puts("");
return;
case 2:
for(int i=x;i<x+k;i++)printf("%d ",i-base);
puts("");
for(int i=1;i<=k;i++)printf("%d ",y-base);
puts("");
return;
}
}
int getmx()
{
int res=0;
for(int i=minx;i<maxx+k;i++)
for(int j=miny;j<maxy+k;j++)
{
res=max(res,Map[i][j]);
Map[i][j]=0;
}
return res;
}
int main()
{
int T;scanf("%d",&T);
while(T--)
{
pre_work();
scanf("%d%s",&k,ch+1);
n=strlen(ch+1);
Map[base][base]=1;
for(int i=1;i<=n;i++)
{
switch(ch[i])
{
case 'N':N();break;
case 'S':S();break;
case 'W':W();break;
case 'E':E();break;
}
minx=min(x,minx);
miny=min(y,miny);
maxx=max(x,maxx);
maxy=max(y,maxy);
}
getxy();
printf("%d\n",getmx());
}
return 0;
}
rp++
