[CSP-S模拟测试]:凤凰院凶真(LCIS)
题目描述
$\alpha$世界线。
凤凰院凶真创立了反抗$SERN$统治的组织“瓦尔基里”。为了脱离$\alpha$线,他需要制作一个世界线变动率测量仪。
测量一个世界线相对于另一个世界线的变动率,实质上就是要求出这两个世界线的最长公共合法事件序列。
一个世界线的事件逻辑序列是一个正整数序列,第$k$个数表示第$k$个事件发生的时间。
对于一个世界线,一个合法的事件序列是事件逻辑序列的一个子序列,满足时间严格递增。
现在,对于两个不同的世间线$\alpha,\beta$,求出最长的一个事件序列,满足这个序列在$\alpha,\beta$世界线中均是合法的。这个序列也就是之前提到过的最长公共合法事件序列。
输入格式
第一行一个整数$n$,表示$\alpha$世界线的事件个数。
第二行$n$个整数$a_1,a_2,...,a_n$,表示$\alpha$世界线的事件逻辑序列。
第三行一个整数$m$,表示$\beta$世界线的事件个数。
第四行$m$个整数$b_1,b_2,...,b_m$,表示$\beta$世界线的事件逻辑序列。
输出格式
第一行一个整数$k$,表示最长公共合法事件序列的长度。
第二行$k$个整数,表示最长公共合法事件序列。如果有多解,输出任意一个。
样例
样例输入:
5
1 4 2 5 1
4
1 1 2 4
样例输出:
2
1 4
数据范围与提示
无论执迷过去
还是叹息未来
皆是不准有丝毫误算的必然
所以本题将捆绑测试。也就是说,只有你通过一个子任务内的所有测试点,才能获得该子任务的全部分数,否则得$0$分。
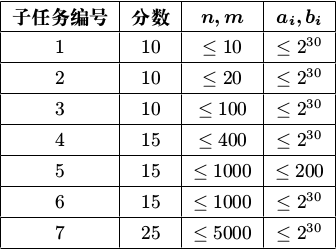
对于$100\%$的数据,$1\leqslant n,m\leqslant 5,000,1\leqslant a_i,b_i\leqslant 2^{30}$。
题解
发现是一道裸的$LCIS$,只不过我们需要在转移的时候记录一下是从哪里转移过来的就好了。
当然要是你闲的慌的话也可以打个三维偏序……
没什么好说的了……
时间复杂度:$\Theta(n^2)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[5001],b[5001];
int dp[5001][5001];
pair<int,int> pre[5001][5001];
void get(int x,int y)
{
if(!x)return;
get(pre[x][y].first,pre[x][y].second);
printf("%d ",b[y]);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
scanf("%d",&m);
for(int i=1;i<=m;i++)
scanf("%d",&b[i]);
for(int i=1;i<=n;i++)
{
int val=0;
pair<int,int> pv=make_pair(0,0);
for(int j=1;j<=m;j++)
{
if(a[i]==b[j]){dp[i][j]=val+1;pre[i][j]=pv;}
else{dp[i][j]=dp[i-1][j];pre[i][j]=pre[i-1][j];}
if(b[j]<a[i])
if(val<dp[i-1][j])
{
pv=make_pair(i-1,j);
val=dp[i-1][j];
}
}
}
int now=0;
for(int i=1;i<=m;i++)if(dp[n][i]>dp[n][now])now=i;
printf("%d\n",dp[n][now]);
get(n,now);
return 0;
}
rp++


 浙公网安备 33010602011771号
浙公网安备 33010602011771号