[CSP-S模拟测试]:字符消除2(hash+KMP)
题目背景
生牛哥终于打通了“字符消除”,可是他又被它的续集难倒了。
题目传送门(内部题52)
输入格式
第一行$n$表示数据组书。
接下来每行一个字符串。(只包含大写字母)
输出格式
每组数据输出一个$01$串。
样例
样例输入:
3
YDYYDY
JRYJREJRYJR
YDYAKYDY
样例输出:
010010
01001101001
01000010
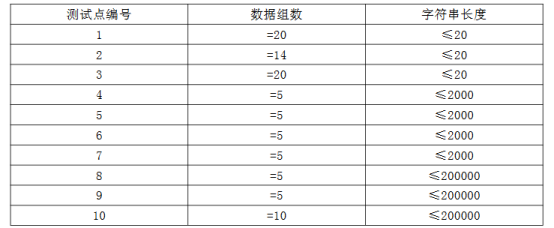
数据范围与提示
题解
为方便,我们设串长为$S$。
首先,来解释一下什么是可行$t$。
对于样例中的第一个串$"YDYYDY"$,我看它比较帅,所以就拿它举例。
它的可行$t$集合为$3$和$6$,为什么呢?
对于一个长度为$3$的环,我们可以这么填:
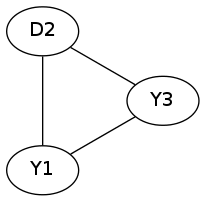
这时,我们填成了一圈,然后我们去填第二圈:
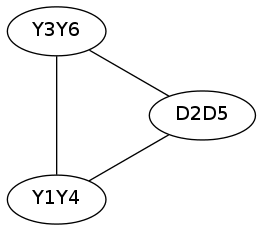
刚好填完,所以它是一个可行$t$,长度为$6$时同理,可是当长度为$4$当我们填到第五个$D$时发现那个位置已经填了$Y$,所以就不可行了。
题意解释完了,我们现在开始考虑这道题应该怎么办?
先来考虑如何求出可行$t$的集合。
我们发现,如果这个串有一个长度为$len$的公共前后缀,那么其中一个可行$t$就是$len-1$,来解释一下:
对于一个公共前后缀,如下图:

橙色区域是公共前后缀,绿色区域是串,显然$a\sim b$点即为长度$len$,那么当我们处理到$c$点时完成了一个环,但是接下来我们要填的$c\sim d$这部分和$a\sim b$是一样的,所以这个$n-len$就是一个长度$t$。
对于$t$的集合,我们可以通过$hash$或者是$KMP$在$\Theta(S)$的时间复杂度内求出。
虽说我用的是$hash$,但是我想讲一下$KMP$如何求出,我们只需要从$n$向前不断的找$next$就好了,也就是$next[next[i]]$,下面来解释为什么:

设橙色区域即$a\sim d$是$next[n]$,也就是说$1-$橙色区域是一组可行$t$,现在另紫色区域即$a\sim b$是$next[next[n]]$,现在来证明$1-$紫色区域是一组可行$t$:
因为$a\sim d$和$e\sim h$相同,$a\sim b$、$c\sim d$、$e\sim f$、$g\sim h$相同,所以我们可以当填一圈填到$g$时接着填完最后$g\sim h$($a\sim b=g\sim h$)。
现在再来考虑如何生成$01$串,显然枚举是不可能的。
设$a$数组表示所有的公共前后缀集合(其实就是$KMP$中的$next$数组),注意不是可行$t$,那么这时候分两种情况:
$\alpha.a[k]\times 2\geqslant a[k+1]$:这时候我们就将$01$串后面接上一段长度为$a[k+1]-a[k]$的后缀即可,如下图:
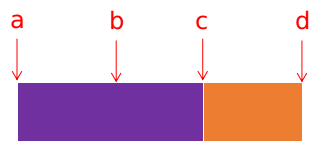
我们现在已经处理好了$a\sim c$这一段,现在要将填$c\sim d$这一段,不妨另$len(b\sim c)=len(c\sim d)$注意现在$c$是$next[d]$,也就是说我们要使$a\sim c=b\sim d$,那么显然是要将$b\sim c$复制到$c\sim d$。
$\beta.a[k]\times 2<a[k+1]$:考虑$next$数组的含义,为了保证解最优,我们一定是先将整个串复制一遍放在最后,然后在中间先填满$0$,如果不行的话将最后一个$0$换成$1$即可,至于如何判断,暴力搞就好了,因为如果$0$不行的话最后以为是$1$肯定行。
这样我们就完美的解决了这道题。
时间复杂度:$\Theta(\sum S)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int n;
char ch[200001];
int b[200001],que[200001],nxt[200001],p;
unsigned long long a[200001],mod[200001];
void pre_work()
{
memset(nxt,0,sizeof(nxt));
memset(b,0,sizeof(b));
p=que[0]=0;
}
void KMP(int l,int r)
{
for(int i=l+1;i<=r;i++)
{
while(p&&b[i]!=b[p+1])p=nxt[p];
if(b[i]==b[p+1])p++;
nxt[i]=p;
}
}
int main()
{
int T;scanf("%d",&T);
mod[1]=1;
for(int i=2;i<=200000;i++)mod[i]=mod[i-1]*131;
while(T--)
{
scanf("%s",ch+1);
pre_work();
n=strlen(ch+1);
a[1]=ch[1]-'A'+1;
for(int i=2;i<=n;i++)
a[i]=a[i-1]*131+ch[i]-'A'+1;
for(int i=0;i<=n;i++)
if(a[i+1]==a[n]-a[n-i-1]*mod[i+2])que[++que[0]]=i+1;
if(que[1]>1)b[que[1]]=1;
KMP(1,que[1]);
for(int i=2;i<=que[0];i++)
{
if(que[i]<=que[i-1]<<1)
{
for(int j=que[i-1]+1;j<=que[i];j++)
b[j]=b[j+que[i-1]-que[i]];
KMP(que[i-1],que[i]);
}
else
{
KMP(que[i-1],que[i]-que[i-1]-1);
int now=p,zero=1,len=que[i]-que[i-1];
while(now)
{
if(!b[now+1]&&!(len%(len-now-1))){b[len]=1;break;}
now=nxt[now];
}
if(!b[now+1]&&!(len%(len-now-1)))b[len]=1;
KMP(len-1,len);
nxt[len]=p;
len=que[i]-que[i-1];
for(int j=1;j<=que[i-1];j++)b[len+j]=b[j];
KMP(len,len+que[i-1]);
}
}
for(int i=1;i<=n;i++)printf("%d",b[i]);
puts("");
}
return 0;
}
rp++


