[CSP-S模拟测试]:reverse(数位DP)
题目描述
我们定义:
$\overline{d_k...d_2d_1}=\sum \limits_{i=1}^kd_i\times {10}^{i-1}=n(d_i\in [0,9]\ and\ d_i\in Z)$
我们对于任何正整数,定义一个函数:
$reverse(\overline{d_1d_2...d_k})=\overline{d_k...d_2d_1})$
比如:$reverse(123)=321,reverse(1000)=1,reverse(520)=25$。
现在,给出两个正整数$L,R$,请求出下面这个集合的大小:
$\{ n\in Z |L\leqslant n\leqslant R\ and\ L\leqslant reverse(n)\leqslant R\}$
输入格式
第一行包含三个整数$T,a,b$分别表示测试数据组数,特殊性质$1$,特殊性质$2$(如果该组数据包含特殊性质$1$,则$a=1$,否则$a=0$;如果该组数据包含特殊性质$2$,则$b=1$,否则$b=0$)。
接下来$T$行每行包含两个整数$L,R$。
输出格式
对于每组数据,输出一行,包含一个整数表示答案。
样例
样例输入:
3 0 0
1 10
10 20
123 12345
样例输出:
10
1
9952
数据范围与提示
对于所有数据,$T=50$。
特殊性质$1$:$L=1$。
特殊性质$2$:$R={10}^k$(即所有$R$都是$10$的整数次幂)
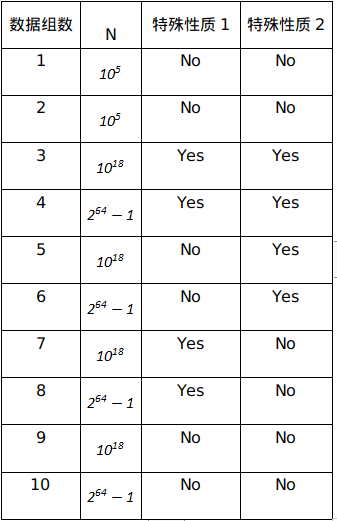
令$1\leqslant L\leqslant R\leqslant N$。
题解
$20\%$算法:
暴力枚举就好啦,不做过多解释。
时间复杂度:$\Theta(T\times(R-L))$。
期望得分:$20$分。
实际得分:$20$分。
另外$20\%$算法:
满足两个特殊性质,考虑从这里入手,$L=1$就说明所有的数都可以,$R={10}^k$说明所有小于等于它的书也都可以,那么第$3,4$个测试点的答案就是$R$。
时间复杂度:$\Theta(T)$。
期望得分:$20$分。
实际得分:$20$分。
$100\%$算法:
发现我们可以计算出$[1,L-1]$中和$[1,R]$中符合条件的数的个数。
那么考虑数位$DP$,定义$dp[i][j]s_1][s_2]$表示 计算了$i$位,当前的前缀长度都是$j$,并且将前缀$reverse$后与$L$和$R$的后$j$位比较结果为$s_1,s_2$,后面的选择有多少种($s_1,s_2$表示大于,等于,小于)。
最后注意,数据范围是$2^{64}-1$,所以我们需要用到一个东西叫做$unsigned\ long\ long$。
时间复杂度:$\Theta(T\times$状态数$\times 10)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
unsigned long long L,R;
unsigned long long dp[22][22][3][3];
int pre_num1[22],pre_num2[22],pro_num[22];
unsigned long long dfs(int pos,int revp,int cmpl,int cmpr,bool lim)
{
if(!pos)
{
if(revp<pre_num1[0]+1)cmpl=0;
if(revp<pre_num2[0]+1)cmpr=0;
return cmpl&&cmpr!=2;
}
if(dp[pos][revp][cmpl][cmpr]!=-1&&!lim)return dp[pos][revp][cmpl][cmpr];
int flag=lim?pro_num[pos]:9;
unsigned long long res=0;
for(int i=0;i<=flag;i++)
{
int ncl,ncr;
if(i==pre_num1[revp])ncl=cmpl;
else ncl=i>pre_num1[revp]?2:0;
if(i==pre_num2[revp])ncr=cmpr;
else ncr=i>pre_num2[revp]?2:0;
res+=dfs(pos-1,revp+1,ncl,ncr,lim&&i==flag);
}
if(!lim)dp[pos][revp][cmpl][cmpr]=res;
return res;
}
unsigned long long calc(unsigned long long x)
{
if(!x)return 0;
memset(dp,-1,sizeof(dp));
memset(pro_num,0,sizeof(pro_num));
while(x)
{
pro_num[++pro_num[0]]=x%10;
x/=10;
}
unsigned long long res=0;
for(int i=pre_num1[0];i<=pro_num[0];i++)
{
int flag=i==pro_num[0]?pro_num[i]:9;
for(int j=1;j<=flag;j++)
{
int ncl,ncr;
if(j==pre_num1[1])ncl=1;
else ncl=j>pre_num1[1]?2:0;
if(j==pre_num2[1])ncr=1;
else ncr=j>pre_num2[1]?2:0;
res+=dfs(i-1,2,ncl,ncr,i==pro_num[0]&&j==flag);
}
}
return res;
}
int main()
{
int T,a,b;
scanf("%d%d%d",&T,&a,&b);
while(T--)
{
scanf("%llu%llu",&L,&R);
unsigned long long l=L,r=R;
memset(pre_num1,0,sizeof(pre_num1));
memset(pre_num2,0,sizeof(pre_num2));
while(l){pre_num1[++pre_num1[0]]=l%10;l/=10;}
while(r){pre_num2[++pre_num2[0]]=r%10;r/=10;}
printf("%llu\n",calc(R)-calc(L-1));
}
return 0;
}
rp++


