[CSP-S模拟测试]:轰炸行动(bomb)(塔尖+拓扑排序+语文)
题目描述
战狂也在玩《魔方王国》。他只会征兵而不会建城市,因此他决定对小奇的城市进行轰炸。
小奇有n座城市,城市之间建立了$m$条有向的地下通道。战狂会发起若干轮轰炸,每轮可以轰炸任意多个城市。
每座城市里都有战狂部署的间谍,在城市遭遇轰炸时,它们会通过地下通道撤离至其它城市。非常不幸的是,在地道里无法得知其它城市是否被轰炸,如果存在两个不同的城市$i$,$j$,它们在同一轮被轰炸,并且可以通过地道从城市$i$到达城市$j$,那么城市$i$的间谍可能因为撤离到城市$j$而被炸死。为了避免这一情况,战狂不会在同一轮轰炸城市$i$和城市$j$。
你需要求出战狂最少需要多少轮可以对每座城市都进行至少一次轰炸。
输入格式
第一行两个整数$n$,$m$。接下来$m$行每行两个整数$a$,$b$表示一条从$a$连向$b$的单向边。
输出格式
一行一个整数表示答案。
样例
样例输入1:
5 4
1 2
2 3
3 1
4 5
样例输出1:
3
样例输入2:
10 10
3 4
5 4
7 1
6 5
6 4
7 4
1 7
5 8
1 2
9 10
样例输出2:
3
数据范围与提示
对于20%的数据,$n,m\leqslant 10$。
对于40%的数据,$n,m\leqslant 1,000$。
对于另外30%的数据,保证无环。
对于100%的数据,$n,m\leqslant 1,000,000$。
题解
这显然是一道语文题,那么我先来解释一下题意。
这道题所说的不能同时炸的两座城市当且仅当城市$i$能到达城市$j$,或城市$j$能到达城市$i$,而不是说城市$i$有一条边能直接指向城市$j$,反之同理。
如下图中,点$1$虽不能直接到达点$4$和$5$,但是可以通过点$2$间接到达点$4$和$5$,所以这张图需要炸$5$次,而不是$3$次。
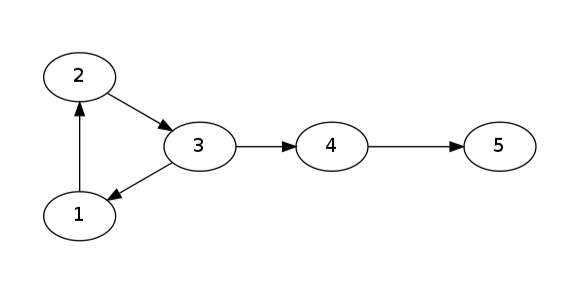
回归到这道题,首先,你可能会想到拓扑排序,用拓扑排序分层,一共有几层就需要炸几次。
那么问题来了,这道题会出现有环的情况,当然是塔尖啦,可以知道,一个环只能一个一个炸,不可能有两个可以一起炸,那么我们在缩环的时候记录一下环的大小即可。
题是简单题,语文不好才是硬伤。
再次印证了那句话:得语文者得$OI$,得语文者得天下!
时间复杂度:$\Theta(n+m)$。
期望的分:$100$分。
实际的分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct rec
{
int nxt;
int to;
}e[2000001],wzc[20000001];
int head[1000001],headw[1000001],cnt,cntw;
int n,m;
int dfn[1000001],low[1000001],sta[1000001],ins[1000001],c[1000001],d[1000001],size[1000001],num,top,tot;
queue<pair<int,int> > q;
int ans;
void add(int x,int y)
{
e[++cnt].nxt=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void add_w(int x,int y)
{
wzc[++cntw].nxt=headw[x];
wzc[cntw].to=y;
headw[x]=cntw;
}
void tarjan(int x)//缩点
{
dfn[x]=low[x]=++num;
sta[++top]=x;
ins[x]=1;
for(int i=head[x];i;i=e[i].nxt)
{
if(!dfn[e[i].to])
{
tarjan(e[i].to);
low[x]=min(low[x],low[e[i].to]);
}
else if(ins[e[i].to])
low[x]=min(low[x],dfn[e[i].to]);
}
if(dfn[x]==low[x])
{
tot++;
int y;
do
{
y=sta[top--];
ins[y]=0;
c[y]=tot;
size[tot]++;//记录环的大小
}while(x!=y);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++)
if(!dfn[i])tarjan(i);
for(int x=1;x<=n;x++)
for(int i=head[x];i;i=e[i].nxt)
if(c[x]!=c[e[i].to])
{
add_w(c[x],c[e[i].to]);//建新图
d[c[e[i].to]]++;
}
for(int i=1;i<=tot;i++)
if(!d[i])
q.push(make_pair(i,1));
while(q.size())//拓扑排序
{
pair<int,int> flag=q.front();
q.pop();
ans=max(ans,flag.second);
if(!--size[flag.first])//跑出了环
{
for(int i=headw[flag.first];i;i=wzc[i].nxt)
{
d[wzc[i].to]--;
if(!d[wzc[i].to])
q.push(make_pair(wzc[i].to,flag.second+1));
}
}
else q.push(make_pair(flag.first,flag.second+1));//注意环的大小
}
cout<<ans<<endl;
return 0;
}
rp++

