[CSP-S模拟测试]:辣鸡(ljh) (暴力)
题目描述
辣鸡$ljh\ NOI$之后就退役了,然后就滚去学文化课了。
然而在上化学课的时候,数学和化学都不好的$ljh$却被一道简单题难住了,受到了大佬的嘲笑。
题目描述是这样的:
在一个二维平面上有一层水分子,请问形成了多少个氢键?
这个二维平面可以看做一个类似棋盘的东西,每个格子可以容纳一个水分子,左下角的格子为$(0,0)$,这个格子右边的格子为$(1,0)$,上方格子为$(0,1)$,以此类推。
辣鸡$ljh$当然不会做了,所以他来求助$JeremyGou$,$JeremyGou$一眼就看穿了真相,并想用这道题来考一考正在做$NOIP$模拟赛的你。
注:在本题中,我们认为一个水分子能与和它曼哈顿距离为$2$且直线距离小于$2$的其他格子形成氢键。
输入格式
一个整数$n$。
接下来$n$行,每行给出四个整数$x_1,y_1,x_2,y_2$。
表示以$(x_1,y_1)$为左下角,$(x_2,y_2)$为右上角的矩形中每个格子都有一个水分子。
给出的所有矩形没有交集。
输出格式
一个整数,表示氢键的数量。
样例
样例输入1:
3
0 0 0 0
0 1 1 2
2 2 2 3
样例输出1:
5
样例输入2:
10
1 8 8 9
0 3 10 7
0 0 7 0
0 2 9 2
4 10 8 10
10 0 10 2
0 10 0 10
8 0 9 1
0 8 0 9
9 8 10 8
样例输出2:
157
数据范围与提示
样例$1$解释:
左图为水分子的排布,右图中的绿色线条表示氢键。
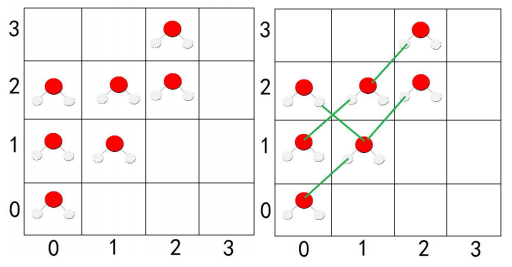
$N\leqslant {10}^5$。
$x\leqslant {10}^9$。
$y\leqslant {10}^9$。
自己画的样例$2\downarrow$:
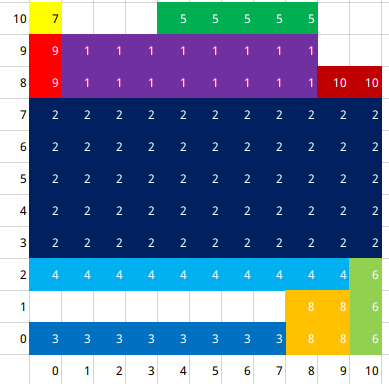
题解
$15\%$算法:
开一个临接矩阵,存一下,在里面$\Theta(\max(x_{2_i},y_{2_i})^2)$跑一遍就好了。
$35\%$算法:
$\Theta(n^2)$枚举每对矩形,统计它们之间形成的贡献,在加上它们内部的贡献即可。
$65\%$算法:
$\Theta(n)$枚举每个矩形,输出它们的内部贡献,即$(x_2-x_1)\times(y_2-y_1)\times 2$,是不是很震惊?!?!
$100\%$算法:
先按$x_1$的大小排个序,然后再进行$\Theta(n^2)$进行枚举,如果$x_j-x_i>1$则$break$。
统计答案的时候分4种情况:
$\alpha.$每个矩形自己内部的贡献。
$\beta.$两个矩形左右相接。
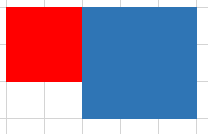
if(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1)>=0)
{
if(e[i].y2==e[j].y1-1)
{
ans+=(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1))<<1;
if(e[i].x1!=e[j].x1)ans++;
if(e[i].x2!=e[j].x2)ans++;
}
if(e[j].y2==e[i].y1-1)
{
ans+=(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1))<<1;
if(e[i].x1!=e[j].x1)ans++;
if(e[i].x2!=e[j].x2)ans++;
}
}
$\chi.$两个矩形上下相接。
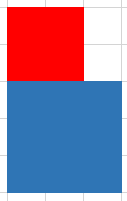
if(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1)>=0)
{
if(e[i].x2==e[j].x1-1)
{
ans+=(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1))<<1;
if(e[i].y1!=e[j].y1)ans++;
if(e[i].y2!=e[j].y2)ans++;
}
if(e[j].x2==e[i].x1-1)
{
ans+=(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1))<<1;
if(e[i].y1!=e[j].y1)ans++;
if(e[i].y2!=e[j].y2)ans++;
}
}
$\delta.$两个矩形对角
if(e[i].x2==e[j].x1-1&&(e[i].y2==e[j].y1-1||e[i].y1==e[j].y2+1))ans++;
这就是正解?!?!
没错,至少出题人这么说的;而对于这道题,出题人就是老大……
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct rec
{
int x1;
int y1;
int x2;
int y2;
}e[100001];
long long ans;
bool cmp1(rec a,rec b){return a.x1<b.x1;}
int main()
{
int n;
scanf("%d",&n);
for(register int i=1;i<=n;i++)
{
scanf("%d%d%d%d",&e[i].x1,&e[i].y1,&e[i].x2,&e[i].y2);
ans+=1LL*(e[i].x2-e[i].x1)*(e[i].y2-e[i].y1);
}
ans<<=1;
sort(e+1,e+n+1,cmp1);
for(register int i=1;i<n;i++)
for(register int j=i+1;j<=n;j++)
{
if(e[j].x1-e[i].x2>1)break;
if(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1)>=0)
{
if(e[i].y2==e[j].y1-1)
{
ans+=(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1))<<1;
if(e[i].x1!=e[j].x1)ans++;
if(e[i].x2!=e[j].x2)ans++;
}
if(e[j].y2==e[i].y1-1)
{
ans+=(min(e[i].x2,e[j].x2)-max(e[i].x1,e[j].x1))<<1;
if(e[i].x1!=e[j].x1)ans++;
if(e[i].x2!=e[j].x2)ans++;
}
}
if(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1)>=0)
{
if(e[i].x2==e[j].x1-1)
{
ans+=(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1))<<1;
if(e[i].y1!=e[j].y1)ans++;
if(e[i].y2!=e[j].y2)ans++;
}
if(e[j].x2==e[i].x1-1)
{
ans+=(min(e[i].y2,e[j].y2)-max(e[i].y1,e[j].y1))<<1;
if(e[i].y1!=e[j].y1)ans++;
if(e[i].y2!=e[j].y2)ans++;
}
}
if(e[i].x2==e[j].x1-1&&(e[i].y2==e[j].y1-1||e[i].y1==e[j].y2+1))ans++;
}
printf("%lld",ans);
return 0;
}
rp++


 浙公网安备 33010602011771号
浙公网安备 33010602011771号