[CSP-S模拟测试]:回家（塔尖）

题目传送门（内部题7）

---

输入格式

第一行一个整数$T$，表示共$T$组数据。
对于每组数据，第一行两个数$n,m$表示有$n$个建筑物，$m$条道路。
接下来$m$行，每行两个整数$u,v$，表示第$u$个建筑物和第$v$个建筑物之间相连。

---

输出格式

对于每组数据，输出共两行。
第一行一个数$x$表示共有$x$个必经点（不包括$1$号点和$n$号点）。
接下来一行$x$个数，描述这$x$个必经点是那些点。按从小到达输出。
注意：如果第一行输出了$0$,那么接下来你输出的第二行应该只有一个换行符。

---

样例

样例输入1：

1
4 3
1 2
2 3
3 4

样例输出1：

2
2 3

样例输入2：

1
5 5
1 2
2 3
3 4
4 5
4 1

样例输出2：

1
4

---

数据范围与提示

$T\leqslant 10$。

$n\leqslant 200,000$。

可能有重边或自环。$m\leqslant n$。

---

题解

是到这道题，首先，应该想到割点，塔尖缩点必不可少。

但是，必经点一定是割点，但是割点不一定是必经点，因为只有在圆方树上1到n这条链上的点才是必经点。

那么我们应该怎么办呢？

显然可以塔尖缩点，建图，在新图上跑，再找回去，但是实现过于复杂，常数较大。

所以我们考虑另一种做法。

在塔尖算法中，如果一个点的时间戳小于等于它的子节点的回溯值，那它一定是一个割点。

那么，如果一个点的儿子的时间戳小于等于n的时间戳的话才是1到n的路径上的必经点。

你可能会仍给我类似下面这张图：

 

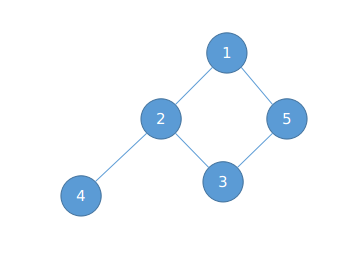
如果我们先访问了点$2$，那么点$3$和点$4$的时间戳都比点$5$小，怎么办呢？

访问了点$2$，如果我们先访问了点$3$，那么点$4$还没有被访问过，而点$4$恰恰是判定点$2$为割点的条件，而此时点$2$连割点的条件都没有满足，更不用考虑是不是必经点了。

如果我们先访问了点$4$，那么点$5$还没有被访问到，所以也不成立。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec
{
	int nxt;
	int to;
}e[1000000];
int head[200001],cnt;
int n,m;
int dfn[200001],low[200001],tot;
bool cut[200001];
int ans;
void pre_work()
{
	cnt=tot=ans=0;
	for(int i=1;i<=n;i++)
		head[i]=dfn[i]=low[i]=cut[i]=0;
}
void add(int x,int y)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	head[x]=cnt;
}
void tarjan(int x)
{
	dfn[x]=low[x]=++tot;
	int flag=0;
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(!dfn[e[i].to])
		{
			tarjan(e[i].to);
			low[x]=min(low[x],low[e[i].to]);
			if(dfn[x]<=low[e[i].to]&&dfn[e[i].to]<=dfn[n])//加一个判定条件
			{
				flag++;
				if(x!=1||flag>1){ans++;cut[x]=1;}
			}
		}
		else low[x]=min(low[x],dfn[e[i].to]);
	}
}
int main()
{
	int T;
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);
		pre_work();
		for(int i=1;i<=m;i++)
		{
			int u,v;
			scanf("%d%d",&u,&v);
			add(u,v);
			add(v,u);
		}
		tarjan(1);
		printf("%d\n",ans);
		for(int i=1;i<=n;i++)
			if(cut[i])printf("%d ",i);
		puts("");
	}
	return 0;
}

不管你怎么说，反正我觉得这个代码比其他人的代码简洁多了～

---

rp++