[Codeforces 274E]:Mirror Room(模拟)
题目传送门
题目描述
有一个$n\times m$的格子图,其中有一些是黑色的,另一些为白色。
从某个白色格子的中心点向左上($NW$),左下($SW$),右上($NE$),右下($SE$)四个方向中的一个发出一束光线,若光线碰到黑色格子或者墙壁(即边界)会反射。反射情况如图所示:

我们不难发现,光线能穿过的格子总数是可以算出的。假如光线经过了某个格子的中心,则称光线经过了这个格子。求光线经过的格子总数。
由于答案可能很大,请使用$long\ long$的$C++$选手注意:请勿使用$\%lld$,推荐$cout$或者$\%I64d$
输入格式
第一行三个整数$n$、$m$、$k$,接下来$k$行每行两个整数$x_i$和$y_i$,表示第$i$个堵塞的格子的坐标。
最后一行两个整数$x_s,y_s$和一个字符串表示激光发出的方向。$“NE”,“NW”,“SE”,“SW”$分别表示方向$(-1,1),(-1,-1),(1,1),(1,-1)$。
保证输入的堵塞的格子坐标不重复。
输出格式
一行输出光束至少通过一次的空格子数。
样例
样例输入
7 5 3
3 3
4 3
5 3
2 1 SE
样例输出
14
数据范围与提示
$30\%$的数据,$n,m \leqslant 30$。
$60\%$的数据,$n,m \leqslant 1000$。
另$20\%$的数据,$k=0$。
$100\%$的数据,$n,m,k \leqslant 100,000$
题解
$30\%$算法:
我觉得这是这道题的难点所在,因为我到现在还想不出来$30\%$的算法怎么打。
$60\%$算法:
稍加思考,发现如果重复经过了某种状态,肯定已经循环过了一次。
想一想,一共有$n^2$个格子,$4$个方向,那么就有$4 \times n^2$个状态,暴力进去搜就好了。
不过需要注意以下几点:
$1.$只有当当前状态被访问过了才可以跳出,并不是当前格子被访问过了。
$2.$如果当前状态没有被访问过,但是当前格子被访问过了,答案不变。
时间复杂度:$O(4\times n^2)$。
期望得分:$60$分。
实际得分:$60$分。
另$20\%$算法:
考虑$k=0$,意思就是说,中间没有任何堵塞的格子,那么分为一下三种情况:
$1.$如果$n \neq m$,那么不管从那个点往哪个方向出发,都一定把整张图全跑一遍,答案即为$n \times m$,记得开$long long$就好了。
$2.$如果$n=m$,光线沿对角线发射,那么它会射到对角,再反弹回来,答案即为$n$。
$3.$还是$n=m$,但是光线不沿对角线发射,那么它会转一圈,答案即为$2 \times n$。
期望多得分数:$10$分。
$100\%$算法:
看一眼那$10^5$的数据范围,直接存图显然是不能接受的,那么我们这么考虑这个问题,用一个set存图,然后每次用二分法计算出下一个转向的位置,将答案加上,转向次数是$O(n+m+k)$级别的,每次查询是$O(\log k)$级别的,那么我们的理论最劣时间复杂度为:$O((n+m+k)\log k)$。
根据题目中光线反射的方式,可以发现,每当光线沿$NW$、$SE$方向前进时,只会经过一种颜色的网格,每当光线沿$NE$、$SW$方向前进时,只会经过另一种颜色的网格。所以光线在某一个格子中心时,要么只会是$NW$、$SE$方向之一,要么只会是$NE$、$SW$方向之一,所以一个点最多只会被经过两次。
易知,如果光线在前进过程中出现过如下两种反射,所有格子就会被经过两次。
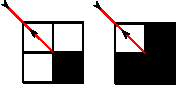
只需在模拟的过程中记录是否出现过这两种情况即可。
代码时刻
$60\%$算法:
#include<bits/stdc++.h>
using namespace std;
int n,m,k;
int ans;
bool Map[1001][1001];//记录堵塞
bool vis[1001][1001][5];//记录状态
void dfs(int x,int y,int w)
{
if(vis[x][y][w])//出现了已经访问过的状态
{
printf("%d",ans);
exit(0);
}
if(!vis[x][y][1]&&!vis[x][y][2]&&!vis[x][y][3]&&!vis[x][y][4])ans++;//如果这个点还没有被经过过
vis[x][y][w]=1;//标记这种状态已经出现过
if(w==1)//四个方向
{
if(!Map[x-1][y+1]){dfs(x-1,y+1,1);return;}//四种情况,小心别打错就好了
if((Map[x-1][y]&&Map[x][y+1])||(!Map[x-1][y]&&!Map[x][y+1])){dfs(x,y,4);return;}
if(Map[x-1][y]){dfs(x,y+1,3);return;}
if(Map[x][y+1]){dfs(x-1,y,2);return;}
}
if(w==2)
{
if(!Map[x-1][y-1]){dfs(x-1,y-1,2);return;}
if((Map[x][y-1]&&Map[x-1][y])||(!Map[x][y-1]&&!Map[x-1][y])){dfs(x,y,3);return;}
if(Map[x][y-1]){dfs(x-1,y,1);return;}
if(Map[x-1][y]){dfs(x,y-1,4);return;}
}
if(w==3)
{
if(!Map[x+1][y+1]){dfs(x+1,y+1,3);return;}
if((Map[x+1][y]&&Map[x][y+1])||(!Map[x+1][y]&&!Map[x][y+1])){dfs(x,y,2);return;}
if(Map[x+1][y]){dfs(x,y+1,1);return;}
if(Map[x][y+1]){dfs(x+1,y,4);return;}
}
if(w==4)
{
if(!Map[x+1][y-1]){dfs(x+1,y-1,4);return;}
if((Map[x+1][y]&&Map[x][y-1])||(!Map[x+1][y]&&!Map[x][y-1])){dfs(x,y,1);return;}
if(Map[x+1][y]){dfs(x,y-1,2);return;}
if(Map[x][y-1]){dfs(x+1,y,3);return;}
}
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=k;i++)
{
int x,y;
scanf("%d%d",&x,&y);
Map[x][y]=1;
}
int x,y;
char ch[5];//这个稍微开打点,因为输入最后会有'\0'。
scanf("%d%d%s",&x,&y,ch+1);
for(int i=0;i<=n+1;i++)Map[i][0]=Map[i][m+1]=1;//边界
for(int i=0;i<=m+1;i++)Map[0][i]=Map[n+1][i]=1;
if(ch[1]=='N'&&ch[2]=='E')dfs(x,y,1);
if(ch[1]=='N'&&ch[2]=='W')dfs(x,y,2);
if(ch[1]=='S'&&ch[2]=='E')dfs(x,y,3);
if(ch[1]=='S'&&ch[2]=='W')dfs(x,y,4);
return 0;
}
$100\%$算法:
#include<bits/stdc++.h>
using namespace std;
struct rec{int x,y,d;};
int n,m,k;
long long ans;//注意long long
set<int>s1[200010],s2[200010];
map<pair<int,int>,bool>mp;
int getid(int x,int y,int d){return d==1?x-y+m+1:x+y;}
bool same(rec a,rec b){if(a.x==b.x&&a.y==b.y&&a.d==b.d)return 1;return 0;}
bool check(int x,int y){return mp[make_pair(x,y)];}
void add(int x,int y)//标记堵塞
{
s1[getid(x,y,1)].insert(x);
s2[getid(x,y,2)].insert(x);
mp[make_pair(x,y)]=1;
}
pair<rec,int> dfs(rec u)//暴力搜索
{
rec re;
set<int>::iterator it;
if(u.d==1)//四个方向
{
it=s1[getid(u.x,u.y,1)].lower_bound(u.x);it--;//用set和lower_bound在log的时间复杂度内求出答案
re.x=u.x-(abs(*it-u.x)-1);
re.y=u.y-(abs(*it-u.x)-1);
if(check(re.x-1,re.y)&&check(re.x,re.y-1))re.d=3;//枚举情况
else if(check(re.x-1,re.y)){re.y--;re.d=4;}
else if(check(re.x,re.y-1)){re.x--;re.d=2;}
else re.d=3;
}
if(u.d==2)
{
it=s2[getid(u.x,u.y,2)].lower_bound(u.x);it--;
re.x=u.x-(abs(*it-u.x)-1);
re.y=u.y+(abs(*it-u.x)-1);
if(check(re.x-1,re.y)&&check(re.x,re.y+1))re.d=4;
else if(check(re.x-1,re.y)){re.y++;re.d=3;}
else if(check(re.x,re.y+1)){re.x--;re.d=1;}
else re.d=4;
}
if(u.d==3)
{
it=s1[getid(u.x,u.y,1)].lower_bound(u.x);
re.x=u.x+(abs(*it-u.x)-1);
re.y=u.y+(abs(*it-u.x)-1);
if(check(re.x+1,re.y)&&check(re.x,re.y+1))re.d=1;
else if(check(re.x+1,re.y)){re.y++;re.d=2;}
else if(check(re.x,re.y+1)){re.x++;re.d=4;}
else re.d=1;
}
if(u.d==4)
{
it=s2[getid(u.x,u.y,2)].lower_bound(u.x);
re.x=u.x+(abs(*it-u.x)-1);
re.y=u.y-(abs(*it-u.x)-1);
if(check(re.x+1,re.y)&&check(re.x,re.y-1))re.d=2;
else if(check(re.x+1,re.y)){re.y--;re.d=1;}
else if(check(re.x,re.y-1)){re.x++;re.d=3;}
else re.d=2;
}
return make_pair(re,abs(*it-u.x));
}
bool judge(rec u)
{
rec re=u;
do
{
pair<rec,int> cur=dfs(u);
ans+=(long long)cur.second;
switch(cur.first.d)//转向
{
case 1:if(u.d==3)return 0;break;
case 2:if(u.d==4)return 0;break;
case 3:if(u.d==1)return 0;break;
case 4:if(u.d==2)return 0;break;
}
u=cur.first;
}while(!same(re,u));
return 1;
}
void pre_build()//处理边界
{
for(int i=0;i<=m+1;i++)
{
add(0,i);
add(n+1,i);
}
for(int i=1;i<=n;i++)
{
add(i,0);
add(i,m+1);
}
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
pre_build();
for(int i=1;i<=k;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
}
int x,y,d;
char ch[5];
scanf("%d%d%s",&x,&y,ch+1);
if(ch[1]=='N'&&ch[2]=='W')d=1;
if(ch[1]=='N'&&ch[2]=='E')d=2;
if(ch[1]=='S'&&ch[2]=='E')d=3;
if(ch[1]=='S'&&ch[2]=='W')d=4;
rec st={x,y,d};
st=dfs(st).first;
if(!judge(st))//开始模拟
{
ans--;
switch(st.d)
{
case 1:st.d=3;break;
case 2:st.d=4;break;
case 3:st.d=1;break;
case 4:st.d=2;break;
}
judge(st);
}
printf("%lld",ans);
return 0;
}
rp++

