STL大全
排序最速传说——sort
我们都学过一些排序的写法,比如冒泡排序,快速排序之类的东西,举个例子来说吧,这是快速排序的代码:
#include<iostream>
using namespace std;
int a[100001];
void quicksort(int l,int r)
{
int i=l,j=r;
int mid=a[(l+r)/2];
do
{
while(a[i]<mid) i++;
while(a[j]>mid) j--;
if(i<=j)
{
swap(a[i],a[j]);
i++;j--;
}
}while(i<=j);
if(l<j) quicksort(l,j);
if(r>i) quicksort(i,r);
}
int main()
{
int arr=0;
int n;
cin>>n;
for(int i=1;i<=n;++i)
cin>>a[i];
quicksort(1,n);
for(int i=1;i<=n;++i)
{
arr++;
if(arr==1) cout<<a[i];
else cout<<" "<<a[i];
}
return 0;
}
而这个操作,sort只要一行
sort(a+1,a+1+n);
a是要排序的数组的名称,+1的意思是从下标为1的开始,+n+1的含义是从1到n。然后a数组中1-n的元素都被排序好了。
sort默认是从小到大排序,但是如果你想让他从大到小排序的话也可以,只需要这样做
int bool cmp(int a,int b)
{
return a>b;
}
sort(a+1,a+n+1,cmp);
同理你也可以在cmp中进行其他的修改,让他可以对结构体进行排序。
为什么说是最速传说?据说这东西吸了氧谁都比不过。
“超级数组”map
map可以对两个元素形成映射关系,先来看他的定义、
map<int,int>mp;
map后面的尖括号里面的两个分别表示下标和存储数据的类型(如果当一个数组来用的话),也就是说,用这个当数组,甚至可以用字符串当下标,当然只有这一点是不足以让他成为超级数组的,正常情况下,开1e9的数组是肯定会爆的,但是,我们的map他没存储东西的数组是不占空间的,所以能完成下面的操作:
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
map<int,int>mp;
mp[1000100000]=114514;
cout<<mp[1000100000]<<endl;
return 0;
}
运行结果:
所以他才被成为超级数组。
但是这个东西有一个很大的缺陷就是在数据很多的时候跑的很慢,所以能用普通数组解决的问题不会用map。
最后提一嘴:unordered_map和map的区别的话,map里面是用hash映射,前者不会排序,所以在效率上要高于普通的map。
精简结构体——pair
pair这个东西我不常用,因为一般pair能干的结构体也可以做,但还是有必要了解一下的。
pair可以存放两个元素,使用的时候直接调用,调用下面再说
先来看一下定义
pair<int,int>p;
看到这个是不是有点眼熟?像极了map,pair的尖括号里面分别表示存放的两个数据的类型
调用的时候也是非常的方便
int p1=p.first;
int p2=p.second;
这样就可以分别调用p存放的两个数据了。
在定义pair的时候,如果觉得一直pair<int,int>太麻烦了,你可以用自带的一个函数,
make_pair(1,1);
我并不觉得很方便,我一般不用。
队列
给你一个左右开口的容器,左进右出,可以知道先进去的一定先出来,所以可以用他的一些性质来实现一些操作,比如bfs就需要用到队列。
手写队列比较麻烦,这里贴一下代码自行体会
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+10,maxn2=31*maxn;
int q[maxn];
int hh,tt;
int main()
{
int m;
cin>>m;
hh=1;
tt=0;
while(m--)
{
char op[11];
cin>>op;
if(!strcmp(op,"push"))
{
int x;
cin>>x;
q[++tt]=x;
}
else if(!strcmp(op,"pop"))
{
hh++;
}
else if(!strcmp(op,"empty"))
{
if(hh<=tt)
cout<<"NO"<<endl;
else
cout<<"YES"<<endl;
}
else if(!strcmp(op,"query"))
{
cout<<q[hh]<<endl;
}
}
}
当然一般情况下我们都不用这么麻烦因为c++有个自带的STL函数叫queue,直接把队列的相关操作打包好了,用这个东西需要 #include <queue> ,但是我习惯用万能头,下面是关于queue的几个常用操作
q.back()返回最后一个元素
q.empty()如果队列空则返回真
q.front()返回第一个元素
q.pop()删除第一个元素
q.push()在末尾加入一个元素
q.size()返回队列中元素的个数
当然还有其他的用法,并且有很多地方可以用这个来节省一些时间,但这不是这篇文章的重点。
栈
栈就是一个只有上面有开口的容器,进来出去都只能用这一个口,容易发现最后进去的反而会最先出来,然后我们就可以利用这个东西来进行一些操作比如关于后缀表达式之类的问题。
中缀表达式
就是最常见的我们日常使用的表达式,比如:\(1+(2+3)\times 4-5\).
中缀表达式是一种通用的算术或逻辑公式表示方法,操作符以中缀形式处于操作数的中间。中缀表达式是人们常用的算术表示方法。
虽然人的大脑很容易理解与分析中缀表达式,但对计算机来说中缀表达式却是很复杂的,因此计算表达式的值时,通常需要先将中缀表达式转换为前缀或后缀表达式,然后再进行求值。对计算机来说,计算前缀或后缀表达式的值非常简单。
前缀表达式
前缀表达式的运算符位于两个相应操作数之前,前缀表达式又被称为前缀记法或波兰式。
像上面的式子由中缀转成前缀就是:\(- + 1 \times + 2 3 4 5\)
或许加个括号更好理解他的运算顺序:\((- (+ 1( \times (+ 2 3) 4)) 5)\)
md怎么好像更乱了
那么如何计算前缀表达式的值呢?
- 从右至左扫描表达式
- 遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 \(op\) 次顶元素),并将结果入栈
- 重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果
示例:
计算上面举例的表达式的值。
- 从右至左扫描,将\(5\),\(4\),\(3\),\(2\)压入堆栈;
- 遇到\(+\)运算符,弹出\(2\)和\(3\)(\(2\)为栈顶元素,\(3\)为次顶元素),计算\(2+3\)的值,得到\(5\),将\(5\)压入栈;
- 遇到\(\times\)运算符,弹出\(5\)和\(4\),计算\(5\times 4\)的值,得到\(20\),将\(20\)压入栈;
- 遇到\(1\),将\(1\)压入栈;
- 遇到\(+\)运算符,弹出\(1\)和\(20\),计算\(1+20\)的值,得到\(21\),将\(21\)压入栈;
- 遇到\(-\)运算符,弹出\(21\)和\(5\),计算\(21-5\)的值,得到\(16\)为最终结果
可以看到,用计算机计算前缀表达式是非常容易的,不像计算后缀表达式需要使用正则匹配
当然这个一般不用
后缀表达式
这才是重点。
后缀表达式与前缀表达式类似,只是运算符位于两个相应操作数之后,后缀表达式也被称为后缀记法或逆波兰式.
例如上面那个中缀表达式转成后缀就是:\(1 2 3 + 4 \times + 5 -\)
与前缀表达式类似,只是顺序是从左至右:
- 从左至右扫描表达式
- 遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素\(op\) 栈顶元素 ),并将结果入栈
- 重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
示例:
计算上面举例的表达式的值
- 从左至右扫描,将\(1\),\(2\),\(3\)压入栈;
- 遇到\(+\)运算符,\(3\)和\(2\)弹出,计算\(2+3\)的值,得到\(5\),将\(5\)压入栈;
- 遇到\(4\),将\(4\)压入栈
- 遇到\(\times\)运算符,弹出\(4\)和\(5\),计算\(5\times4\)的值,得到\(20\),将\(20\)压入栈;
- 遇到\(+\)运算符,弹出\(20\)和\(1\),计算\(1+20\)的值,得到\(21\),将\(21\)压入栈;
- 遇到\(5\),将\(5\)压入栈;
- 遇到\(-\)运算符,弹出\(5\)和\(21\),计算\(21-5\)的值,得到\(16\)为最终结果
ybt计算后缀表达式的值
当然这里需要用栈。
code:
远古时代马蜂
#include<bits/stdc++.h>
using namespace std;
int a[99];
stack<long long>q;
int main()
{
string s;
getline(cin,s);
long long len=s.size(),o=0,p=1;
for(int i=0;i<len-1;i++)
{
if(s[i]>='0'&&s[i]<='9')
{
a[o]=s[i]-48;
o++;
}
else if(s[i]==' ')
{
long long b=0;
while(o--)
{
b+=a[o]*p;
p*=10;
}
o=0;p=1;
q.push(b);
}
else if(s[i]=='/')
{
long long y=q.top();
q.pop();
long long x=q.top();
q.pop();
q.push(x/y);
}
else if(s[i]=='*')
{
long long y=q.top();
q.pop();
long long x=q.top();
q.pop();
q.push(x*y);
}
else if(s[i]=='-')
{
long long y=q.top();
q.pop();
long long x=q.top();
q.pop();
q.push(x-y);
}
else if(s[i]=='+')
{
long long y=q.top();
q.pop();
long long x=q.top();
q.pop();
q.push(x+y);
}
}
cout<<q.top()<<endl;
return 0;
}
ybt计算中缀表达式
这里我们需要先把中缀表达式转成后缀表达式,然后再进行计算,因为中缀表达式对我们来说很好算,但计算机并不擅长。
code:
同上的远古代码
#include<bits/stdc++.h>
using namespace std;
stack<int>shu;
stack<char>q;
string s;
int len;
inline int level(char ch)
{
if(ch=='-'||ch=='+')return 1;
if(ch=='*'||ch=='/')return 2;
return 0;
}
inline void yunsuan()
{
int a=shu.top();shu.pop();
int b=shu.top();shu.pop();
char ch=q.top();q.pop();
if(ch=='-')shu.push(b-a);
if(ch=='+')shu.push(b+a);
if(ch=='*')shu.push(b*a);
if(ch=='/')shu.push(b/a);
}
void solve()
{
int x=0,flag=0;
for(int i=0;i<len;i++)
{
if(s[i]>='0'&&s[i]<='9')
{
x=x*10+(s[i]-'0');
flag=1;
}
else
{
if(flag)
{
shu.push(x);
x=0;
flag=0;
}
if(s[i]=='(')
{
q.push(s[i]);
continue;
}
if(s[i]==')')
{
while(q.top()!='(') yunsuan();
q.pop();
continue;
}
while(!q.empty()&&level(q.top())>=level(s[i]))yunsuan();
q.push(s[i]);
}
}
if(flag)
shu.push(x);
while(!q.empty())
yunsuan();
cout<<shu.top()<<endl;
}
bool check()
{
if(len==1)return level(s[0])>0?0:1;
for(int i=1;i<len;i++)
if(level(s[i])&&level(s[i-1]))return 0;
int sum=0;
for(int i=0;i<len;i++)
{
if(s[i]=='(')sum++;
if(s[i]==')')sum--;
}
return sum==0;
}
int main()
{
cin>>s;
len=s.size()-1;
if(!check())
cout<<"NO"<<endl;
else
solve();
return 0;
}
双端队列——deque
deque函数:
deque容器为一个给定类型的元素进行线性处理,像向量一样,它能够快速地随机访问任一个元素,并且能够高效地插入和删除容器的尾部元素。但它又与vector不同,deque支持高效插入和删除容器的头部元素,因此也叫做双端队列。deque类常用的函数如下。
(1) 构造函数
deque():创建一个空deque
deque(int nSize):创建一个deque,元素个数为nSize
deque(int nSize,const T& t):创建一个deque,元素个数为nSize,且值均为t
deque(const deque &):复制构造函数
(2) 增加函数
void push_front(const T& x):双端队列头部增加一个元素X
void push_back(const T& x):双端队列尾部增加一个元素x
iterator insert(iterator it,const T& x):双端队列中某一元素前增加一个元素x
void insert(iterator it,int n,const T& x):双端队列中某一元素前增加n个相同的元素x
void insert(iterator it,const_iterator first,const_iteratorlast):双端队列中某一元素前插入另一个相同类型向量的[forst,last)间的数据
(3) 删除函数
Iterator erase(iterator it):删除双端队列中的某一个元素
Iterator erase(iterator first,iterator last):删除双端队列中[first,last)中的元素
void pop_front():删除双端队列中最前一个元素
void pop_back():删除双端队列中最后一个元素
void clear():清空双端队列中最后一个元素
(4) 遍历函数
reference at(int pos):返回pos位置元素的引用
reference front():返回手元素的引用
reference back():返回尾元素的引用
iterator begin():返回向量头指针,指向第一个元素
iterator end():返回指向向量中最后一个元素下一个元素的指针(不包含在向量中)
reverse_iterator rbegin():反向迭代器,指向最后一个元素
reverse_iterator rend():反向迭代器,指向第一个元素的前一个元素
(5) 判断函数
bool empty() const:向量是否为空,若true,则向量中无元素
(6) 大小函数
Int size() const:返回向量中元素的个数
int max_size() const:返回最大可允许的双端对了元素数量值
(7) 其他函数
void swap(deque&):交换两个同类型向量的数据
void assign(int n,const T& x):向量中第n个元素的值设置为x
两个栈底的栈——双端栈
他并不是STL。
双端栈是指将一个线性表的两端当做栈底分别进行入栈和出栈操作.
在顺序栈的共享技术中,最常用的就是两个栈共享,即双端栈。利用栈底位置不变,栈顶变化的特性。首先申请一个一维数组空间,data[n],将两个栈的栈低分别放在数组的两端,分别是0和n-1,由于是栈顶动态变化的,这样可以形成互补,使得每个栈可用的最大空间与需求有关,由此可见,两个共享栈比两个栈分别申请n/2哥空间利用率高。
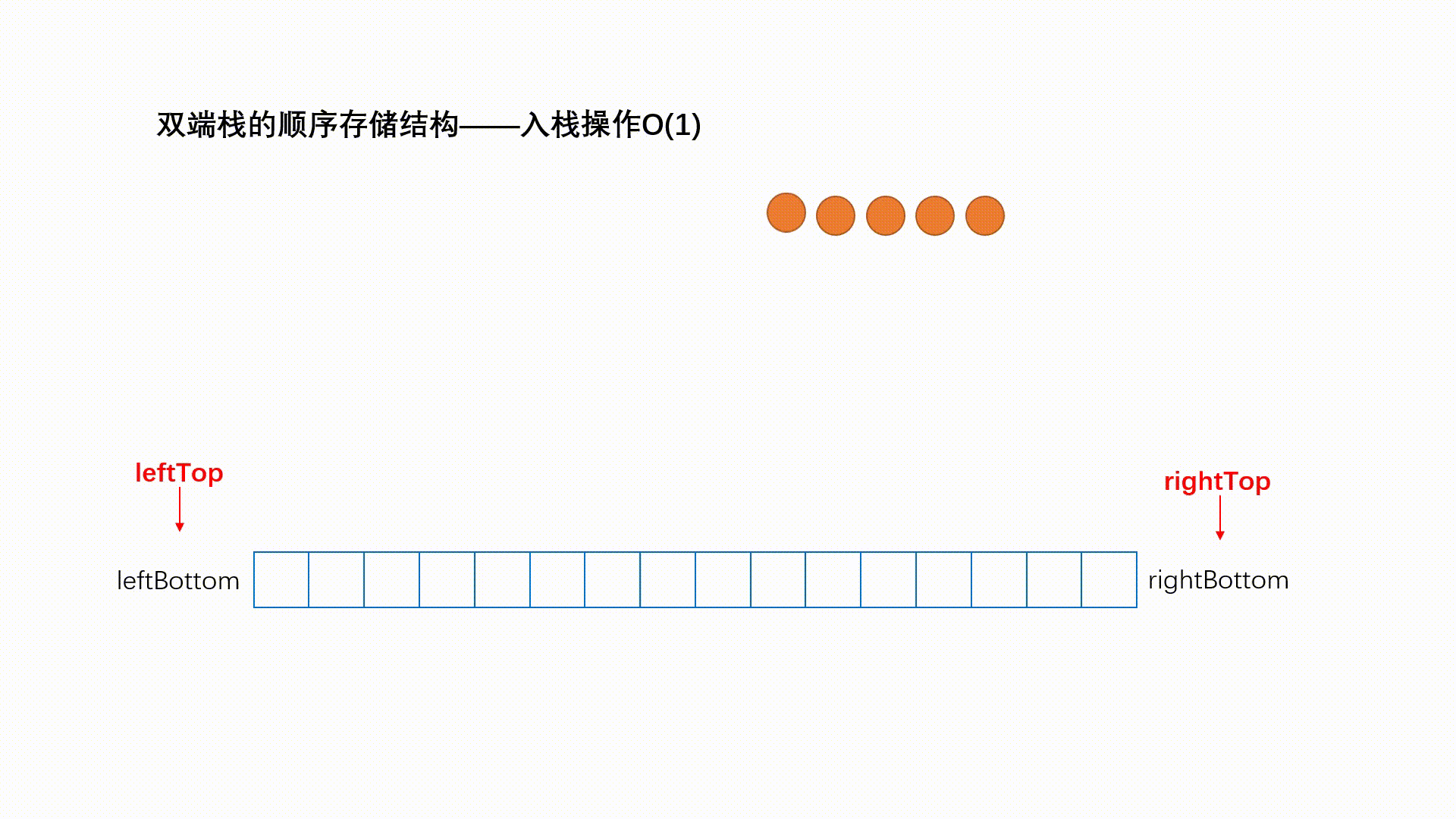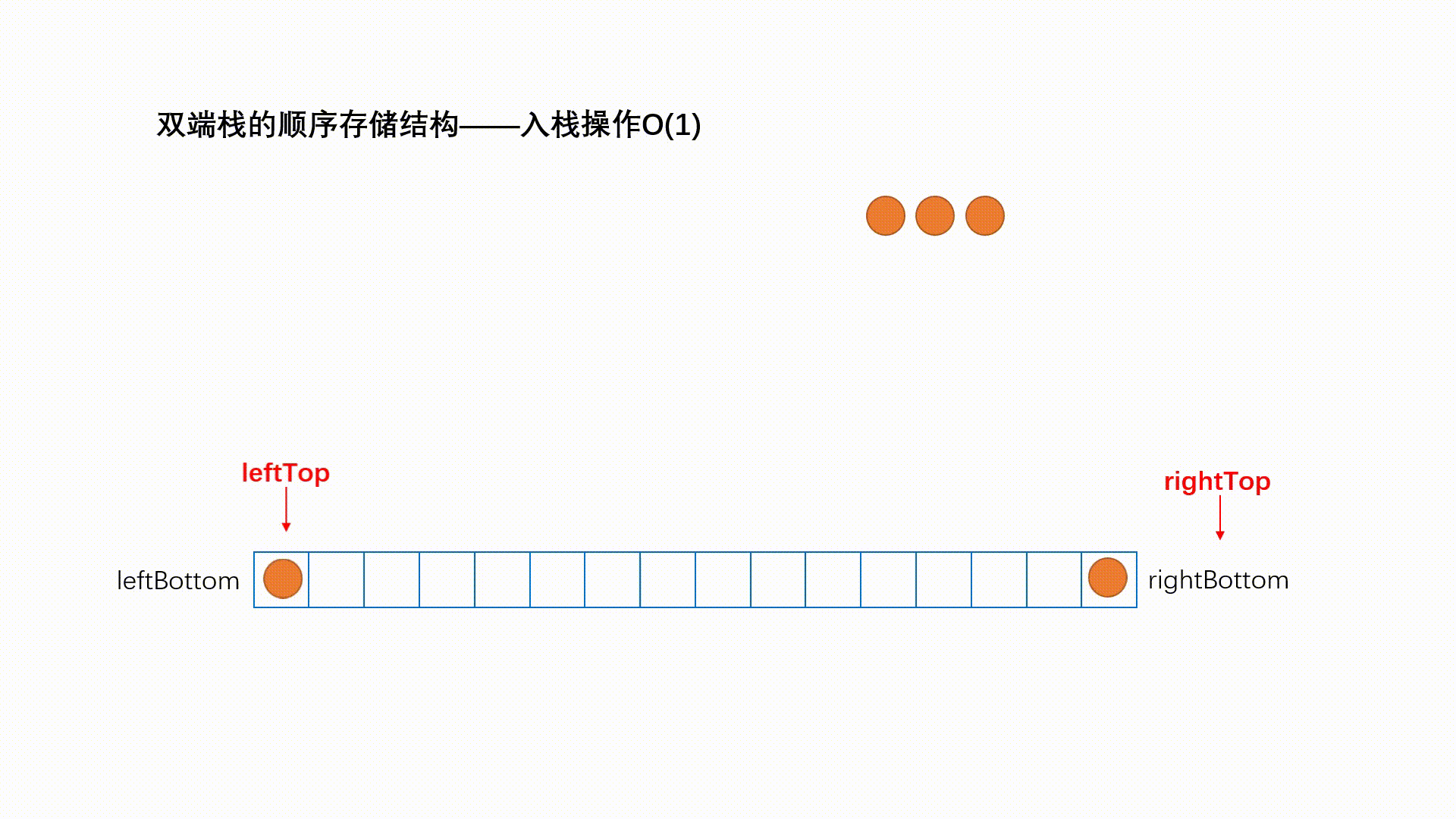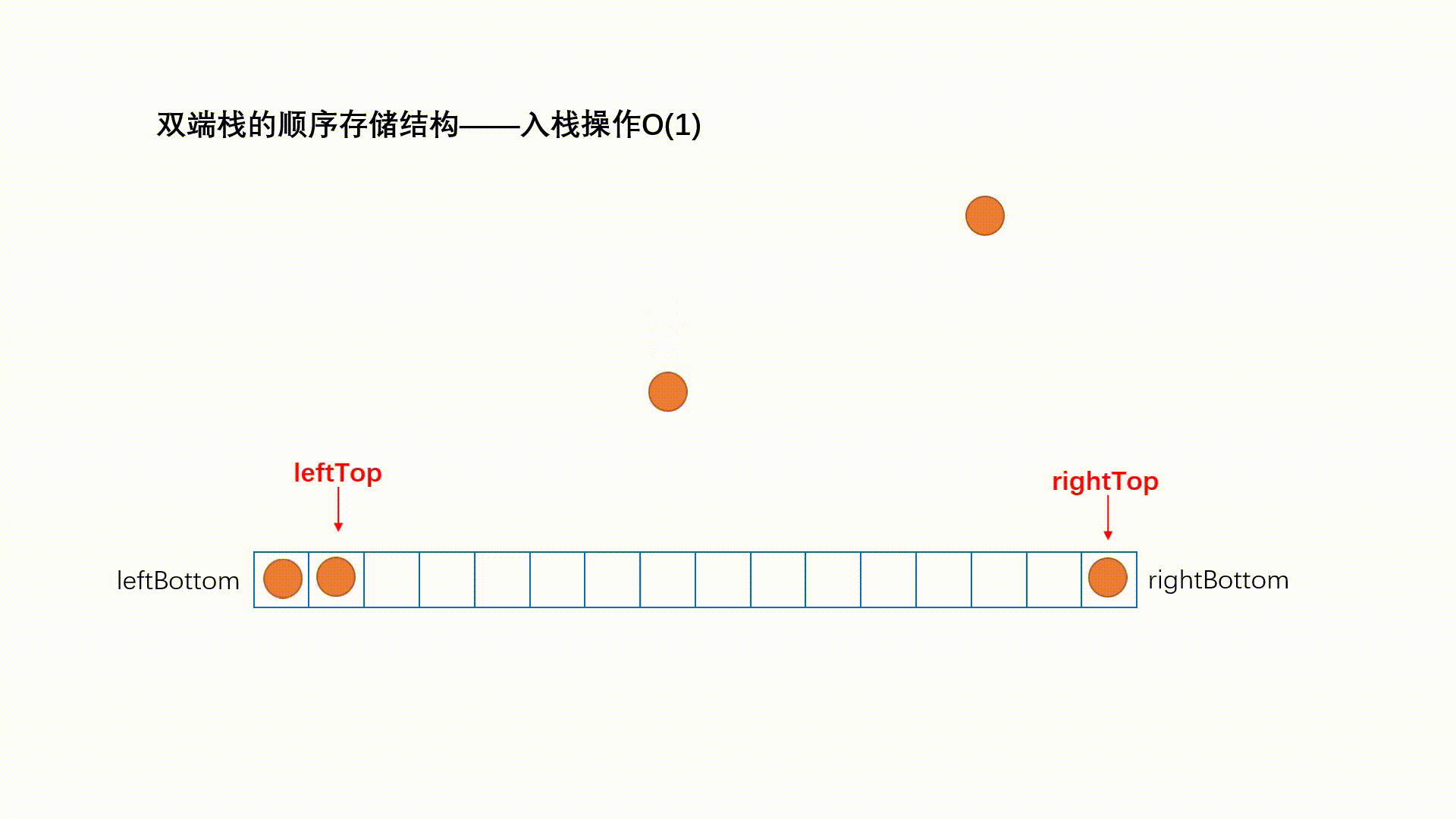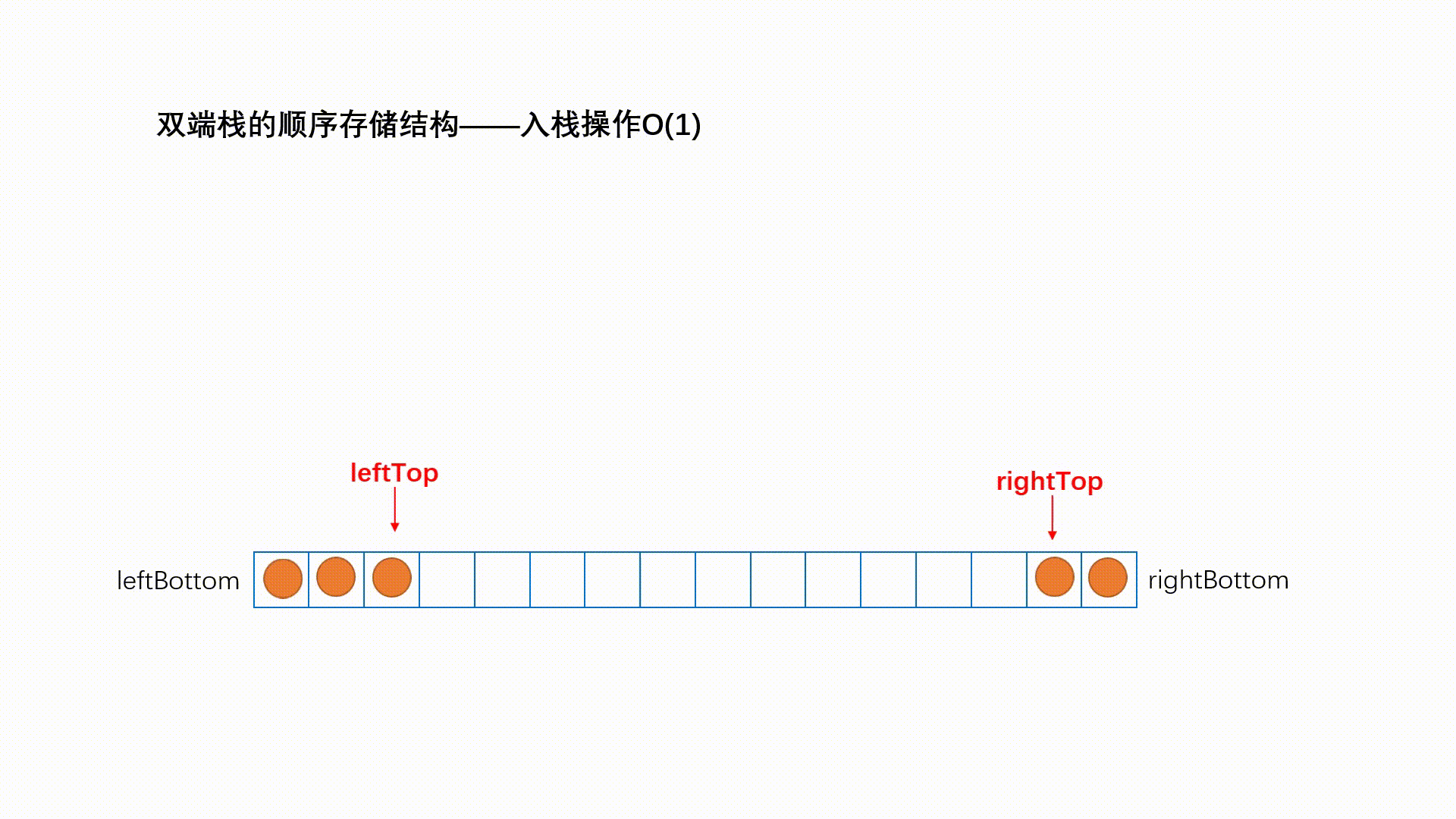
其实我不会但是我要鸽掉了。
本文来自博客园,作者:北烛青澜,转载请注明原文链接:https://www.cnblogs.com/Multitree/p/17002989.html
The heart is higher than the sky, and life is thinner than paper.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号