基环树学习笔记

基环树

以下内容参考：https://www.cnblogs.com/fusiwei/p/13815549.html

概念

基环树也叫环套树，标准定义是一个有 \(n\) 个节点 \(n\) 条边的联通图，如果不是联通的，则称其是一个基环树森林。

例如下面这张图就是一个基环树。

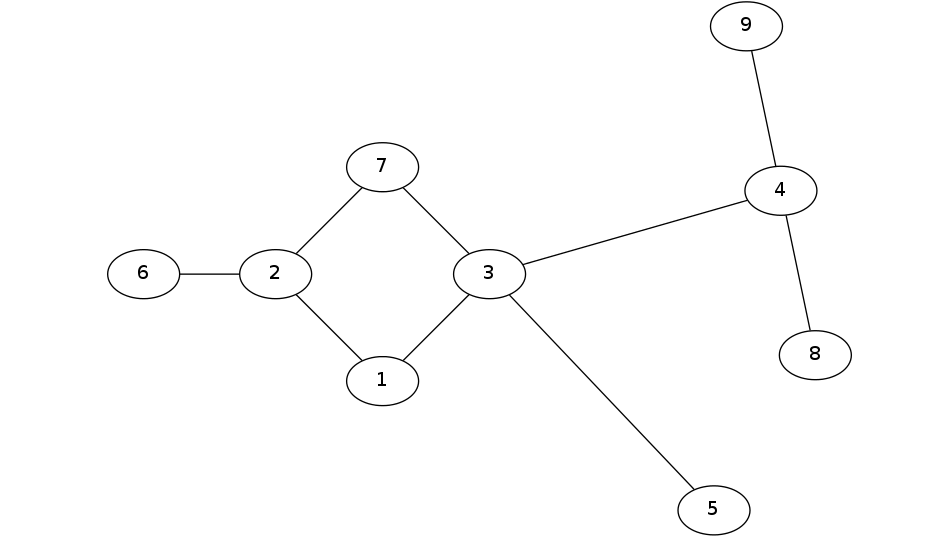
如果我们把里面的环内的任意一条边给断开，他就会变成一棵树，如果把这个环全部断掉则会变成一个森林。

内向树和外向树

所谓内向树的定义是每个点有且只有一条出边。也就是这棵树给人的大体感觉是向内的。

所谓外向树的定义是每个点有且只有一条入边。也就是这棵树给人的大题感觉是外向的。

例如下面这个就是一棵内向树。

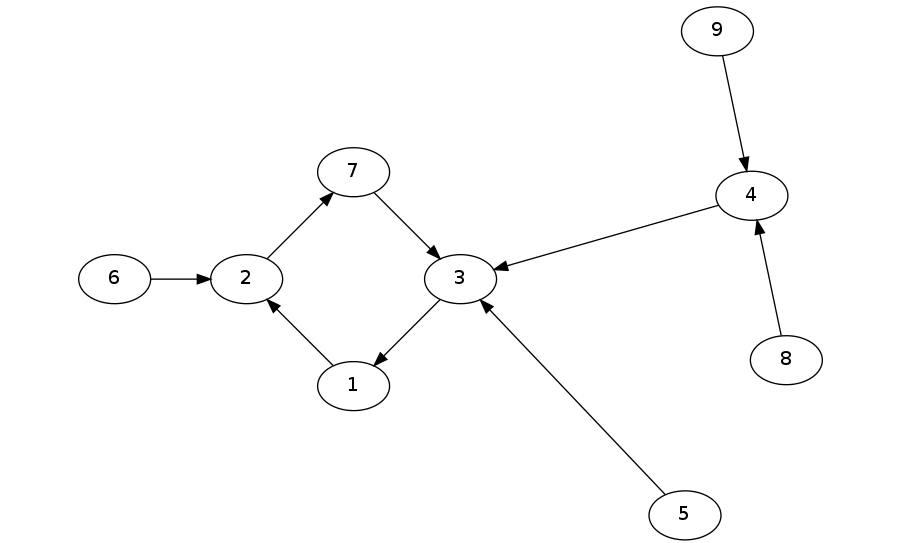
而下面这个就是一棵外向树。

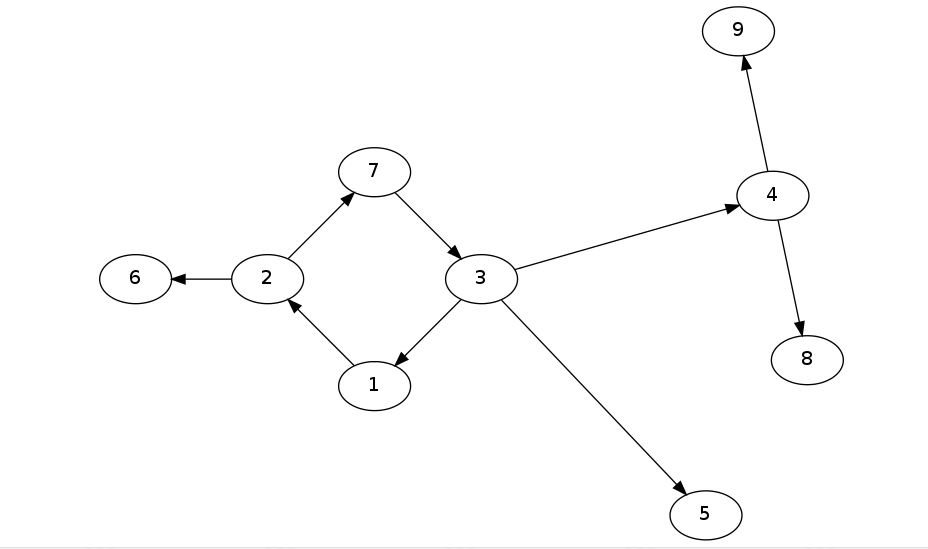
基环树题型

根据上面的定义介绍，我们可以感觉到，基环树虽然被单独拿出来讨论，但是其本质上还是一个比较简单且好理解的数据结构之一。所以它只能适当地提升题目难度，并不能说一个树的题变成基环树就大大增强了。

一些经典例题有：基环树直径、基环树两点之间距离，基环树DP，等。

这些模型的解决通法一般是：断环成树，然后将若干棵树处理好之后，再考虑环对答案的影响。也就是将环、树分开讨论解决问题。这时，用”环套树“这个名词来形容基环树，很是容易理解。

P8655 [蓝桥杯 2017 国 B] 发现环

题目的意思简洁明了，就是让你找一个环，并且要按编号从小到大输出环内的所有点。

我们可以用并查集来判断是否有环，我们边加边边合并，如果当前两个点已经在同一集合内的话，说明已经有环了，且环的所有边都已经加进去了。然后我们再跑一遍 dfs 后直接 sort 一下输出即可。

#include<bits/stdc++.h>
#define int long long
#define N 1001000
using namespace std;
int n,f[N],vis[N];
vector<int>v[N],ans;
inline int fid(int x)
{
	if(f[x]==x)return x;
	return f[x]=fid(f[x]); 
}
inline void merge(int x,int y)
{
	int xx=fid(x);
	int yy=fid(y);
	if(xx!=yy)
	  f[xx]=yy;
}
inline void dfs(int s,int t)
{
	if(s==t)
	{
		sort(ans.begin(),ans.end());
		for(int i=0;i<ans.size();i++)
			cout<<ans[i]<<' ';
		exit(0);
	}
	for(int i=0;i<v[s].size();i++)
	{
		int u=v[s][i];
		if(!vis[u])
		{
			vis[u]=1;
			ans.push_back(u);
			dfs(u,t);
			ans.pop_back();
			vis[u]=0;
		}
	}
}
signed main()
{
	int a,b;
	cin>>n;
	for(int i=1;i<=n;i++)
	  f[i]=i;
	for(int i=1;i<=n;i++)
	{
		cin>>a>>b;
		v[a].push_back(b);
		v[b].push_back(a);
		if(fid(a)!=fid(b))
		  merge(a,b);
		else break;
	}
	vis[a]=1;
	ans.push_back(a);
	dfs(a,b);
	return 0;
}

P8943 Deception Point

根据题目不难发现，就是一棵基环树，只要B比A先到达离A最近的环上的点，那么A是必死的，反之A一定存活，所以我们可以先找出环上所有的点，然后我们在处理出每一个点到最近点所需的步数，然后进行分类讨论:

1. A在环上，B不在，此时A是1000%会存活的
2. A不在环上，B在，此时需要看情况，如果B在A到环上之前堵住的话A就无了。
3. A不在环上，B也不在，跟上面一样计算即可
4. A，B都在环上，A一定存活

至此就可以AC这个题了。

#include<bits/stdc++.h>
#define int long long
#define N 200010
using namespace std;
int n,q,fd,k,vis[N],f[N],dep[N],sw[N],cnt,cir[N];
vector<int>mp[N];
inline void dfs1(int x,int fa)
{
	if(vis[x]==1)//如果当前点已经被搜到过了 
	{
		fd=x;//标记当前点 
		cir[x]=1;//标记此点在环内 
		sw[x]=++cnt;//记录当前点被标记的时间戳 
		return ;//退出 
	}
	vis[x]=1;
	int len=mp[x].size();
	for(int i=0;i<len;i++)
	{
		int v=mp[x][i];
		if(v!=fa)dfs1(v,x);//除父亲外往下搜 
		if(fd)//如果已经找到环 
		{
			if(fd==x)fd=0;//如果回溯到了标记的点就取消标记，防止后面不是环内的点被标记 
			if(!cir[x])//如果当前点没有标记在环内 
			{
				cir[x]=1;//标记 
				sw[x]=++cnt;//打上时间戳 
			}
			break;//退出循环 
		}
	}
}
inline void dfs2(int old,int x,int fa)//old是当前进入的环的点 
{
	f[x]=old;//f存放当前进入环的第一个点 
	dep[x]=dep[fa]+1;//处理深度 
	int len=mp[x].size();
	for(int i=0;i<len;i++)
	{
		int v=mp[x][i];
		if(!cir[v]&&mp[x][i]!=fa)//如果当前点不是父亲或者不是环上的点就继续递归 
		  dfs2(old,v,x);
	}
}
signed main()
{
	cin>>n>>q;
	for(int i=1;i<=n;i++)
	{
		int u,v;
		cin>>u>>v;
		mp[u].push_back(v);
		mp[v].push_back(u);
	}
	dfs1(1,0);
	for(int i=1;i<=n;i++)
	  if(cir[i])//把每一个环上的点都往外搜一遍 
	    dfs2(i,i,0);
	while(q--)
	{
		int x,y;
		cin>>x>>y;
		int u1=f[x],v1=f[y];//取出两个点可以到达的最近的环上的点 
		int len=abs(sw[u1]-sw[v1]);//计算两个环上点的距离 
		if(len>cnt/2)//如果距离长度大于环的一半长度 
			len=cnt-len;//减去计算最近距离 
		if(cir[x]||dep[x]<dep[y]+len)//如果要是逃亡的一开始就在环上或者逃亡的在抓捕者前进入环内 
			cout<<"Survive\n";//可以存活 
		else cout<<"Deception\n";//反之不可以 
	}
	return 0;
}