字典树 Trie
因为某些原因把 xyh 的周记和我的字典树合到一块了。
字典树
Trie 树,即字典树,是一种树形结构。典型应用是用于统计和排序大量的字符串前缀来减少查询时间,最大限度地减少无谓的字符串比较。
Trie 树的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
性质
-
字典树的根节点不代表任一个字符,其余所有节点都包含一个字符。
-
从字典树的根部开始走,路径上所有的字符 串起来就是当前节点所代表的字符串。
-
每一个节点的子节点所代表的字符各不相同。
就像这张图
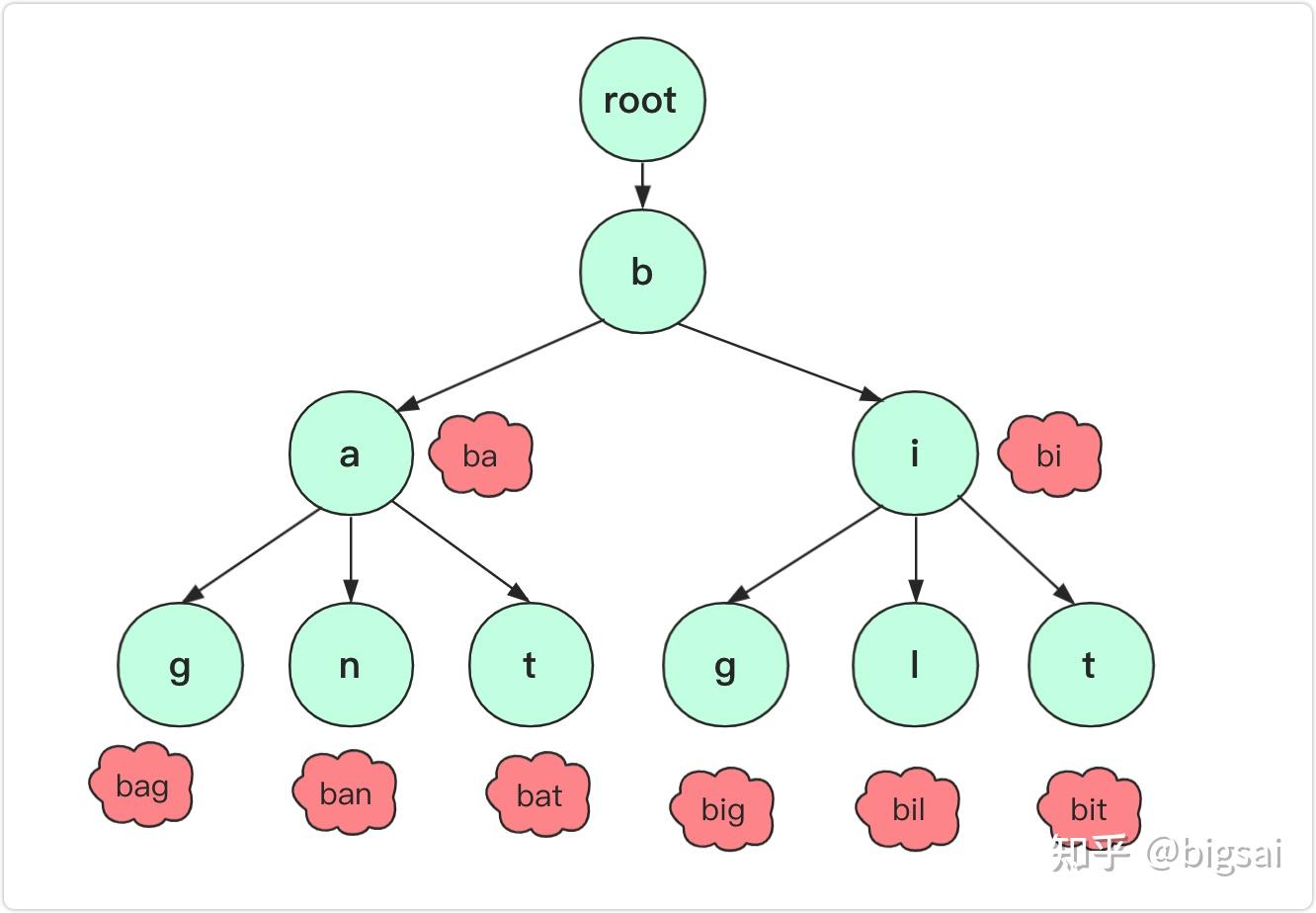
字典树的操作
我们用 t[i][j]来表示第i个点的子节点中的j字符的下一个点。
下面的代码参考都是模板里的,所以可能有一点奇怪
字符转化
首先我们都知道字符是不如数字好处理的,所以我们可以先把字符给转化成字符,因为一般的题目都是大小写英文字母,加起来也就52个,所以我们可以用以下的函数来进行此操作
当然这个东西就是闲的慌才单独写个函数
int getnum(char x)//转换字符
{
if(x>='A'&&x<='Z')
return x-'A';
else if(x>='a'&&x<='z')
return x-'a'+26;
else return x-'0'+52;
}
插入
向字典树里插入一个字符串,我们要从根节点开始,假设一个点 p,初始值为跟节点编号也就是 0,然后先判断当前层是否有对应的字符串第 i 个字符 c ,如果没有的话,我们就标记一下当前层的 c 在本次出现,然后把 p 替换为当前点的编号,也就是新开的点的编号;如果有字符 c 的话,我们可以直接把当前 p 替换为当前点的编号,这样就建出一棵和上方图中一样的字典树了。
void add(string s1)
{
int p=0,len=s1.size();
for(int i=0;i<len;i++)
{
int c=getnum(s1[i]);
if(!t[p][c])
t[p][c]=++idx;
p=t[p][c];
cnt[p]++;
}
}
查询
就拿模板题(下方)为例,我们要找的是当前给你的字符串在字典树中是几个字符串的前缀,也就是从根节点开始,走完给你的字符串,中间如果有的路是不通的,也就是给你的字符串的第 i 个字符在字典树第 i 层没有出现过,那么我们就可以直接返回0,其次,如果最后完整的找了下来,我们需要看看后面的子树大小,然后直接输出
int fid(string s1)
{
int p=0,len=s1.size();
for(int i=0;i<len;i++)
{
int c=getnum(s1[i]);
if(!t[p][c])
return 0;
p=t[p][c];
}
return cnt[p];
}
练习
模板题
本题的大意是给你一堆字符串,然后在问你里面有多少个串去掉后面数个字符后能与给你的字符串相同。
本题最简单的做法就是建一棵字典树,然后按找顺序查询给你的字符串,到了最后一个之后,当前点的子树大小就是答案。
代码实现
#include<bits/stdc++.h>
#define N 3000010
using namespace std;
int T,q,n,t[N][65],cnt[N],idx;
string s;
int getnum(char x)//转换字符
{
if(x>='A'&&x<='Z')
return x-'A';
else if(x>='a'&&x<='z')
return x-'a'+26;
else return x-'0'+52;
}
void add(string s1)
{
int p=0,len=s1.size();
for(int i=0;i<len;i++)
{
int c=getnum(s1[i]);
if(!t[p][c])
t[p][c]=++idx;
p=t[p][c];
cnt[p]++;
}
}
int fid(string s1)
{
int p=0,len=s1.size();
for(int i=0;i<len;i++)
{
int c=getnum(s1[i]);
if(!t[p][c])
return 0;
p=t[p][c];
}
return cnt[p];
}
void qk()
{
for(int i=0;i<=idx;i++)
for(int j=0;j<=122;j++)
t[i][j]=0;
for(int i=0;i<=idx;i++)
cnt[i]=0;
idx=0;
}
int main()
{
cin>>T;
while(T--)
{
qk();
cin>>n>>q;
for(int i=1;i<=n;i++)
{
cin>>s;
add(s);
}
for(int i=1;i<=q;i++)
{
cin>>s;
cout<<fid(s)<<endl;
}
}
return 0;
}
一本通1471
这道题,其实并不难,甚至可以省去专门的查询操作,直接在插入的时候打个标记判断即可,我们看到样例可以发现我们可以从两个方面来讨论这道题,一是当前正在插入的字符串是之前已经插入过的字符串的前缀,那么我们可以想到,如果当前正在插入的字符串的最后一个字符在之前就已经存在,那么就是前缀,有可能你会疑惑,为什么不用考虑前面的,因为前面的如果新开了点,那么后面的点一定也是新开的,第二种情况就是之前插入的字符串是当前插入的字符串的前缀,我们可以开一个数组,用于标记每一个字符串的结束的点,如果在插入当前字符串的时候有一个点是被标记过的,那么就是前缀。其实有第三种情况,也就是两个字符串一样,但这个情况上面两个判断都可以处理。
答应我,清空从0开始而不是1
整整一个小时!!
#include<bits/stdc++.h>
#define N 4000100
using namespace std;
int T,n,t[N][53],vis[N],idx,flag;
string s;
inline int gc(char x){return x-'0';}
inline void add(string s1)
{
int p=0,len=s1.size();
for(int i=0;i<len;i++)
{
int c=gc(s1[i]);
if(t[p][c]&&i==len-1)
{
flag=1;
return ;
}
if(!t[p][c])
t[p][c]=++idx;
p=t[p][c];
if(vis[p])
{
flag=1;
return ;
}
if(i==len-1)
vis[p]=1;
}
return ;
}
void qk()
{
for(int i=0;i<=idx;i++)
{
vis[i]=0;
for(int j=0;j<=10;j++)
t[i][j]=0;
}
idx=flag=0;
}
int main()
{
cin>>T;
while(T--)
{
qk();
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>s;
add(s);
}
if(flag==1)cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
return 0;
}
一本通1472
第一眼看到:这™跟字典树有啥关系?!
我们需要将每一个数都转化为一个32位的二进制数,不够的高位补0,然后我们再对其进行字典树的建树;当我们查询的时候发现同时进行对两个数的查找不是很好操作,所以我们可以降低一点对时间复杂度的要求,比如,我们可以将其中一个数确定下来,也就是,每一次fid函数都找与当前数异或的最大值,然后取一个max,就可以完美AC了。
#include<bits/stdc++.h>
#define N 4001000
using namespace std;
int n,a[N],t[N][2],vis[N],idx,ans;
void add(int x)
{
int p=0;
for(int i=31;i>=0;i--)//从2的32次方开始枚举,默认每一个数转为2进制都是32位,不够用0补齐
{
int c=(x>>i)&1;//取出x的第i+1位
if(!t[p][c])
t[p][c]=++idx;
p=t[p][c];
}
}
int get(int x)
{
int p=0,v=0,ans=0;//p是当前x的下标,v是我们要找的数的下标
for(int i=31;i>=0;i--)//从2的32次方枚举到1次方
{
int c=(x>>i)&1,o;//取出当前x的第i+1位
if(c)o=0;//o是c的相反的那个子节点
else o=1;
if(t[v][o])v=t[v][o],ans=(ans<<1)|1;//尽量选取与当前x的第i+1位不同的数
else v=t[v][c],ans<<=1;
p=t[p][c];
}
return ans;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
add(a[i]);
}
for(int i=1;i<=n;i++)
ans=max(ans,get(a[i]));
cout<<ans<<endl;
return 0;
}
P2922 [USACO08DEC]Secret Message G
题目大意就是给你n个串,然后在给你m个串,问你这m个串中的每一个串与n个串其中一个串是另一个串的前缀的个数是多少。
我们可以看出来这道题和那道ybt的1471差不多,也就是我们在建字典树的时候可以打个标记,每一个字符串的末尾都打上标记,然后在统计数量的时候,路径上把所有的vis都累加起来,最后输出的时候加上以当前节点为根的子树的大小就ok了。
答应我,把你的vis[i]=1换成vis[i]++好吗。
#include<bits/stdc++.h>
#define N 5000100
using namespace std;
int n,m,o,t[N][3],vis[N],idx,cnt[N];
void add(int len)
{
int c,p=0;
for(int i=1;i<=len;i++)
{
cin>>c;
if(!t[p][c])
t[p][c]=++idx;
p=t[p][c];
cnt[p]++;
}
vis[p]++;
}
void fid(int len)
{
int c,p=0,ans=0,flag=1;
for(int i=1;i<=len;i++)
{
cin>>c;
if(flag==0)
continue;
if(vis[p])ans+=vis[p];
if(!t[p][c])
flag==0,t[p][c]=++idx;
p=t[p][c];
}
if(flag==0)
{
cout<<"0"<<endl;
return ;
}
else
{
cout<<(ans+cnt[p])<<endl;
return ;
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>o;
add(o);
}
for(int i=1;i<=m;i++)
{
cin>>o;
fid(o);
}
return 0;
}
P3879 [TJOI2010] 阅读理解
首先考虑如何建树,如果是每一篇短文都建一棵字典树的话,那空间肯定是不够的,所以我们可以想,在vis上面改一下,给他加一维,但是空间还是不够,这时候我们需要用到只占1字节的bool数组:bitset。有了这个,你的vis大小是之前的约1/32!
我们在插入字符串的时候,可以多传一个参数x,表示这个字符串是在第x篇短文里,然后我们在进行查询操作的时候,只要当前的t[p][c]没有出现过,我们就可以直接输出空行;最后的时候,把vis数组从一到n遍历一下输出就可以了。
#include<bits/stdc++.h>
#define N 300100
using namespace std;
int n,m,t[N][26],idx;
string s;
bitset<1010>b[N];
void add(string s1,int x)
{
int p=0;
for(int i=0;i<s1.size();i++)
{
int c=s1[i]-'a';
if(!t[p][c])
t[p][c]=++idx;
p=t[p][c];
}
b[p][x]=1;
}
void fid(string s1)
{
int p=0;
for(int i=0;i<s1.size();i++)
{
int c=s1[i]-'a';
if(!t[p][c])
{
cout<<' '<<endl;
return ;
}
p=t[p][c];
}
for(int i=1;i<=n;i++)
{
if(b[p][i])
cout<<i<<' ';
}
cout<<endl;
return ;
}
int main()
{
int x;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x;
for(int j=1;j<=x;j++)
{
cin>>s;
add(s,i);
}
}
cin>>m;
for(int i=1;i<=m;i++)
{
cin>>s;
fid(s);
}
return 0;
}
正文
在从前有一只小鹅,他住在河边.
在从前有一只小狸,她住在林涧.
沿河散步的小鹅遇到了河边发呆的小狸,他坐到了他的旁边,分享自己的快乐,她看到了旁边的小鹅,交换自己的见闻。
他们成为了好朋友,从那时。
他们每一天一起散步,一起聊天,一起觅食,一起追逐,打闹荡秋千。从早玩到晚,从星星聊到草涧。
他生性贪玩,大大咧咧。她性格内向,谨行慎言。有时他说话不过大脑,做事不过小脑,语出伤人而不自知。她表现得似乎已经习惯,不与他计较,只不过是默默的记在心里。
终于在一个秋天,尘封的火山爆发,她渲泄出积蓄的不满。
可他似乎并不明白他为何恼怒,只觉得他无理取闹,可笑至极便心生气愤。
他们在彼此的愤怒中不欢而散,到了冬天,小河边冷寂。
春天又来,他又遇上了她。他想道歉,她想和好,可是心中的倔强牵制着他们两个,似乎都有一种可笑的自尊心,于是他们从最亲密的伙伴变成了不开口的陌生人。
慢慢的,小鹅长大成了大鹅,可狸猫一直是他心中的别扭。
慢慢的,小狸长大成了狸猫,可大鹅一直是她心中的一个结。
于是她找到了他,他找到了她,他们两个相视一笑,似乎都知道对方在想什么,也知晓对方知道,他们做了一个约定明年春天在这里相见————一个不切实际的约定。
很奇怪的,人总会在注定失去的时候挽留。
不奇怪的,人总会在注定失去的时候挽留。
注:不是博主写的,是博主的同桌xyh写的,在博主看完之后觉得尴尬,他本人强烈要求我发布到网络上。
本文来自博客园,作者:北烛青澜,转载请注明原文链接:https://www.cnblogs.com/Multitree/p/16786189.html
The heart is higher than the sky, and life is thinner than paper.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号