搜索学习笔记

搜索#

重要性#

搜索是一个很好锻炼代码能力的算法，学好搜索，能很好的理解dfs、bfs等，有利于别的算法（图论即与树相关的问题）的实现

关键#

明确当前给你的状态，你需要什么才能往下搜
明确操作是什么
事先思考怎么搜合适，即怎么搜会更快，不要碰到题就开始搜，剪枝也最好在写题前写好想好，剪枝放在一起放在最前面（方便检查修改）
状态：指当前所面临的问题的信息，如当前的位置等信息
转移：指从一个状态到另一状态的一种决策
我们从问题中寻找状态与转移方法！

实质#

一棵树或图
根为其实节点$S$
某些满足终止条件的叶子为终止节点$T$
要求一条满足条件的路径$S->T$，或者找到$T$

思考顺序#

1. 从题目确定状态，目标
2. 从题目确定决策，即每一步做什么
3. 列出基本的框架，思考状态、决策能否简化
4. 剪枝，最优化，可行性

可行性剪枝：判断当前位置能否到T
最优性剪枝：若$f(P)+exp(P)>Ans$，则回溯
$P$为当前状态，$Ans$为已知最优解
$f(P)$为当前代价，$exp(P)$为到$T$期望最小代价
若$exp(P)$难以计算，设为$0$

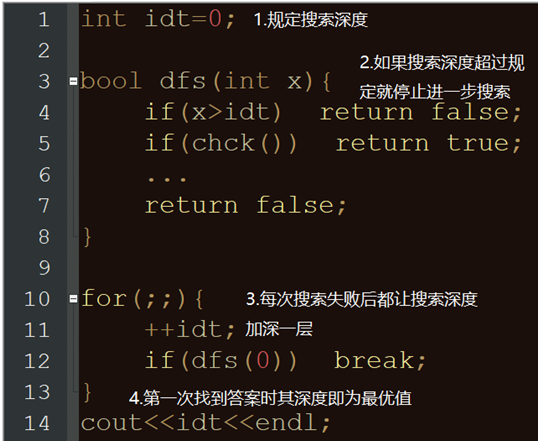
迭代加深搜索#

搜索前设立一个 $Limit$，假设答案不会超过$Limit$
若 $f(P)+exp(P)>Limit$ ，则回溯
搜索失败则加大$Limit$
本质上是深搜和广搜的互补
深搜对于一些答案很浅的问题有时候效率很低
广搜则需要大量的空间，以及难以剪枝
迭代加深搜索则兼具两者的优点

记忆化搜索#

我们一般写的动态规划是bfs模式的，即一个点从与它相邻的点转移过来
如果用深搜写动态规划，就可以说是记忆化
基本思路：
对于每个状态，存储该状态返回信息
以后再到该状态，直接调用存储信息即可
记忆化搜索是另一种动态规划，按划分应该分在动态规划里面，即它的复杂度是确定的
但其优点是很容易想到，思考难度较低，本质上是搜索再加上几行记忆化即可
先考虑搜索怎么搜，再加上记忆化

启发式搜索#

事情开始逐渐不对起来。。
令$G(P)=f(P)+exp(P)$ 作为状态P的启发函数
$exp$ 为到达终止状态期望需要花费的代价
找到最优解即找到一个启发式函数值最小的终止状态
这东西我就没见有人用过

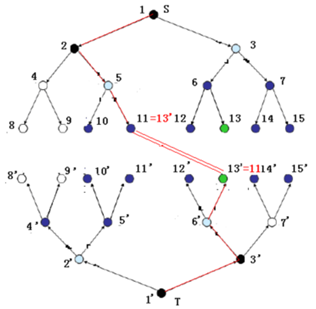
折半搜索#

如果已知起点和终点，可以考虑从起点和终点一起搜，这样可以把指数上的$n$ 除以$2$
主要思想：
两个人分别从$A$地和$B$地出发，向对方出发点走去
当他们都走了$L/2$米时在“中间”相遇
找到了长度为$L$的路径
双向BFS
从起始状态和目标状态同步BFS，直至交汇。
理论上可以将访问到的状态数开根号

优化方法#

一般先考虑消耗较大的决策（类似于先贪心，利用最优性剪枝来加快搜索速度）
如果问题可以分为多个互不相同的子问题，先考虑状态量少的子问题
如果搜索的状态与数值排列的顺序无关，可以考虑把数值排序，在有HASH判重的情况下，这样一般可以再减少一个阶乘的复杂度