Tarjan学习笔寄
tarjan算法
参考博客:
https://www.cnblogs.com/nullzx/p/7968110.html
https://www.cnblogs.com/ljy-endl/p/11562352.html
强连通分量定义
在有向图 \(G\) 中,如果两个顶点 \(u,v\) 之间有一条从 \(u\) 到 \(v\) 的有向路径,同时还有一条从 \(v\) 到 \(u\) 的有向路径,则称两个顶点强联通,如果有向图 \(G\) 的每两个顶点都强联通,则称 \(G\) 是一个强联通图。有向非强联通图的极大强联通子图,称为强联通分量。

有向边按访问情况分为 \(4\) 类:
- 树边:访问节点走过的边,图中的黑色边。
- 返祖边:指向祖先节点的边,图中的红色边。
- 横叉边:右子树指向左子树的边,图中的绿色边。
- 前向边:指向字数中节点的边,图中的蓝色边。
返祖边与树必构成环,横叉边可能与树构成环。
我们在经过一遍 dfs 后就可以得到这样的一棵树:

如果节点 \(x\) 是某个强连通分量在搜索树中遇到的第一个节点,那么这个强连通分量的其余节点肯定是在搜索树中以 \(x\) 为根的子树中。节点 \(x\) 被称为这个强连通分量的根。
tarjan算法缩点
Tarjan算法是基于对图深度优先搜索的算法,每一个强连通分量为搜索树中的一颗子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。定义 \(dfn(u)\) 为节点 \(u\) 搜索的次序编号(时间戳),\(low(u)\) 为 \(u\) 或 \(u\) 的子树能够追溯到的最早的栈中节点的次序号。由定义可以得出,\(low(u)=min(low(u),low(v))\) \((u,v)\) 为树枝边,\(u\) 为 \(v\) 的父节点,\(low(u)=min(low(u),dfn(v))\) \((u,v)\) 为指向栈中节点的后向边(指向栈中节点的横叉边)当节点 \(u\) 搜索结束以后,若 \(dfn(u)=low(u)\) 时,则以 \(u\) 为根的搜索子树上所有还在栈中的节点是一个强连通分量。
缩点的过程就是用深搜来实现的,我们从当前点开始往后找,分三种情况,第一种:如果终点的 \(dfn\) 值为 \(0\) 的话,说明没有遍历过,我们继续往下搜,回溯的时候我们用终点的 \(low\) 值来更新当前点的 \(low\) 值,因为父节点是肯定能到其子树内各个节点的;第二种就是已经遍历过了,但是终点在栈里,所以我们可以用终点的 \(dfn\) 来更新当前点的 \(low\) 值,第三种就是终点是遍历过但不在栈里,说明终点所在的强连通分量已经全部遍历完成,所以不可以用当前终点来更新。当当前点的子树的点都遍历过一次后,如果当前点是他所处的强连通分量的根节点的话,我们就不断弹栈,直到弹到是当前节点为止,我们就把以当前点为强连通分量的点都给处理出来了。
算法过程
从节点 \(1\) 开始 DFS 把遍历到的节点加入栈中。搜索到节点 \(u=6\) 时,\(dfn[6]=low[6]\),找到了一个强连通分量,退栈到 \(u=v\) 为止,{6} 为一个强连通分量。
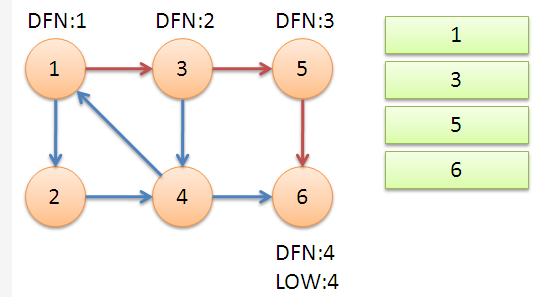
初始化时 \(low[u]=dfn[u]=++index\),返回节点 \(5\),发现 \(dfn[5]=low[5]\),退栈后 {5} 为一个强连通分量。
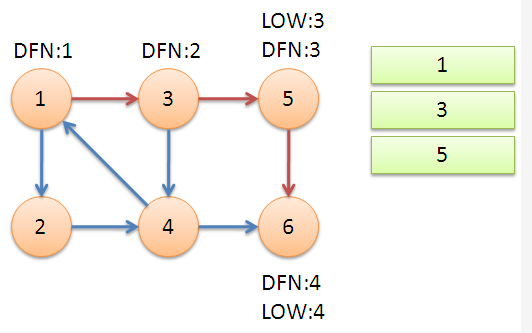
返回节点 \(3\),继续搜索到节点 \(4\),把 \(4\) 加入堆栈。发现节点 \(4\) 向节点 \(1\) 有后向边,节点 \(1\) 还在栈中,所以 \(low[4]=1\)。节点 \(6\) 已经出栈,\((4,6)\) 是横叉边,返回 \(3\),\((3,4)\) 为树枝边,所以 \(low[3]=low[4]=1\)。
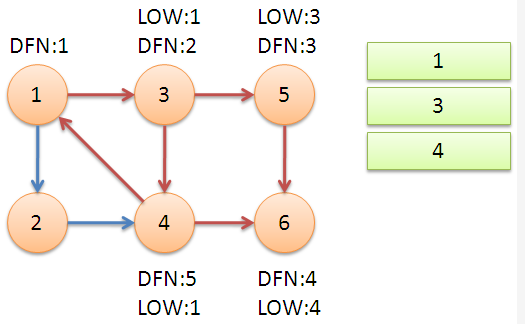
\(low[u]=min(low[u],dfn[u])\) \((u,v)\)为指向栈中节点的后向边。
继续回到节点 \(1\),访问最后的节点 \(2\)。访问边 \((2,4)\),\(4\) 还在栈中,所以 \(low[2]=dfn[4]=5\)。返回 \(1\) 后,发现 \(dfn[1]=low[1]\),把栈中节点全部取出,组成一个强连通分量 {1,3,4,2}。
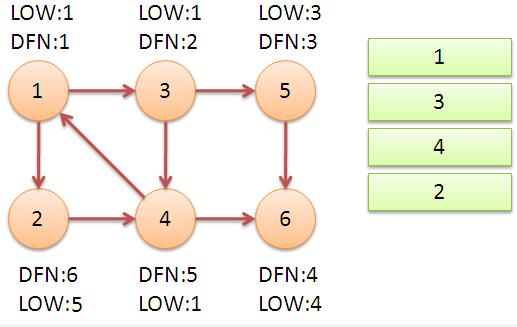
至此算法结束,求出了图中全部的三个强连通分量。
题目练习
来看一道模板题:
这到题就是单纯的模板,所以也比较好实现。
然后我们来考虑如何 A 掉这道题。题目要求的是一条路径,使路径经过的点权值之和最大,而我们只需要求出这个最大权值和。我们在主函数里面正常建图,然后直接开始跑 tarjan ,缩完点后的图再重新建一遍,然后直接开始 dfs(暴搜大法好),输出最大的那个值就 ok 了。
完整代码:
#include<bits/stdc++.h>
#define N 100010
using namespace std;
struct sb{int to,from,next;}e[N],p[N];//ep存两个不同的边
int n,m,a[N],cnt,cnt1,head[N],ans1;//a存放每一个点的点权,ans1存放答案
int st[N],low[N],dfn[N],top,h[N];//st手写栈,low表示当前点所属的强连通分量,dfn表示搜索的顺序
int vis[N],tim,sd[N],f[N];//vis标记是否入栈,sd表示当前点属于哪一个强连通分量,f表示以当前点为起点当前点获得的最大点权和
inline void add(int u,int v)//一开始的建图
{
e[++cnt].from=u;
e[cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;
}
inline void ad(int u,int v)//缩点后的建图
{
p[++cnt1].from=u;
p[cnt1].to=v;
p[cnt1].next=h[u];
h[u]=cnt1;
}
void tarjan(int x)//缩点操作
{
dfn[x]=low[x]=++tim;//当前点默认自己就是一个强连通分量
st[++top]=x;vis[x]=1;//把当前点压入栈中,标记入栈
for(int i=head[x];i;i=e[i].next)//遍历每一个与x相连的边
{
int y=e[i].to;//取出终点
if(!dfn[y])//如果当前点没有被搜索过
{
tarjan(y);//继续搜索终点
low[x]=min(low[x],low[y]);//当前点所属的强连通分量就是当前点和终点所属的强连通分量编号较小的那个
}
else if(vis[y])//如果终点已经在栈中了
low[x]=min(low[x],dfn[y]);//取较小的强连通分量编号
}
if(dfn[x]==low[x])//如果一遍下来当前点的编号与强连通分量的编号一样
{
int y;//y是当前栈顶的元素
while(1)//只要没有到x就一直弹
{
y=st[top--];//用y取出栈顶元素
sd[y]=x;//标记当前点属于x
vis[y]=0;//标记清空
if(x==y)break;//如果到达了x就退出
a[x]+=a[y];//加上y点的点权
}
}
}
int dfs(int k)//dfs
{
if(f[k])return f[k];//如果当前点已经有值了就直接返回值
int ans=0;//存放除当前点以外的最大值
for(int i=h[k];i;i=p[i].next)//遍历每一个与k相连的边
ans=max(ans,dfs(p[i].to));//ans取当前存放的值与走当前边的值的较大值
return f[k]=ans+a[k];//返回的时候加上
}
int main()
{
cin>>n>>m;//n个点,m个边
for(int i=1;i<=n;i++)
cin>>a[i];//输入每一个点的点权
for(int i=1;i<=m;i++)
{
int x,y;
cin>>x>>y;//表示从x到y有一条边
add(x,y);//存有向图
}
for(int i=1;i<=n;i++)//遍历每一个点
if(!dfn[i])//如果当前点的dfn是0
tarjan(i);//开始缩点
for(int i=1;i<=m;i++)//遍历之前建过的边
{
int x=sd[e[i].from];//取出缩点后的起点和终点
int y=sd[e[i].to];
if(x!=y)//如果起点和终点是不一样的
ad(x,y);//建边
}
for(int i=1;i<=n;i++)//枚举每一个点
{
if(!f[sd[i]])//如果以当前点为起点没有值
ans1=max(ans1,dfs(sd[i]));//开始搜索,更新答案
}
cout<<ans1<<endl;//输出答案
return 0;//好习惯
}
再来看一道题目:
这道题目看起来好像挺难的,其实比模板题都简单,模板题里面可以看到跑了一遍 tarjan 后又建了一张图跑的 dfs,但这个题就没这么麻烦,首先要按照题目要求建边,然后跑一遍 tarjan,在标记强连通分量的时候重新开一个计数器,最后把缩完点的边全遍历一遍,终点的入度加一,最后只要统计入度为 \(0\) 的强连通分量的数量即为答案。
代码如下:
#include<bits/stdc++.h>
#define N 100100
using namespace std;
struct sb{int u,v,next;}e[N];//存放建的边
int head[N],cnt,n,low[N],dfn[N],tim;//low表示当前点所属的强连通分量,dfn表示搜索的顺序
int sd[N],st[N],top,t[N],ans,vis[N],num;//vis标记是否入栈,sd表示当前点属于哪一个强连通分量,st是手写栈,t是标记当前强连通分量入度
inline void add(int u,int v)//加边操作
{
e[++cnt].u=u;
e[cnt].v=v;
e[cnt].next=head[u];
head[u]=cnt;
}
void tajian(int x)//tarjan算法主体
{
dfn[x]=low[x]=++tim;//当前点默认自己就是一个强连通分量
st[++top]=x;//把当前点压入栈中,标记入栈
vis[x]=1;
for(int i=head[x];i;i=e[i].next)
{
int y=e[i].v;
if(!dfn[y])//如果当前点没有被搜索过
{
tajian(y);//继续搜索终点
low[x]=min(low[x],low[y]);//当前点所属的强连通分量就是当前点和终点所属的强连通分量编号较小的那个
}
else if(vis[y])//如果终点已经在栈中了
low[x]=min(low[x],dfn[y]);//取较小的强连通分量编号
}
if(dfn[x]==low[x])//如果一遍下来当前点的编号与强连通分量的编号一样
{
int y;//y是当前栈顶的元素
num++;//num是当前的强连通分量编号
while(1)
{
y=st[top--];//用y取出栈顶元素
vis[y]=0;//去除标记
sd[y]=num;//标记当前点属于num
if(x==y)break;//如果到达了x就退出
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
int y;
cin>>y;
while(y!=0)
{
add(i,y);//建边
cin>>y;
}
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tajian(i);//跑tarjan
for(int i=1;i<=cnt;i++)//枚举每一条边
{
int x=sd[e[i].u];//取出起点终点强连通分量编号
int y=sd[e[i].v];
if(x!=y)//如果不是同一个强连通分量
t[y]++;//终点的入度加1
}
for(int i=1;i<=num;i++)//枚举每一种颜色
if(!t[i])//如果当前点的入度为0说明需要新开一个光盘
ans++;//答案加一
cout<<ans<<endl;//输出答案
return 0;//好习惯
}
tarjan算法割点
割点与桥(割边)的定义
在无向图中才有割边和割点的定义
割点:在一个无向联通图中,如果去掉此顶点和与他相连的所有边,图中的联通块(连通块就是一个无向图里面的两个顶点都可以互相到达的无向图)数量增加,则称该顶点为割点。
桥(割边):在无向联通图中,去掉一条边,图中的连通块数量增加,则称这条边为桥或者割边。
割点与桥的关系:
-
有割点不一定有桥,有桥一定存在割点
-
桥链接的两个点中一定有一个点是割点
原理
DFS 是必不可少的。
假设 DFS 中我们从顶点 \(u\) 访问到了顶点 \(v\)(此时顶点 \(v\) 还未被访问过),那么我们称当前的顶点 \(u\) 为顶点 \(v\) 的父顶点(也就是 DFS 时从哪个点搜过来的),\(v\) 是 \(u\) 的孩子顶点。在顶点 \(u\) 之前被访问过的顶点,我们就称之为 \(u\) 的祖先结点。
显然如果顶点 \(u\) 的所有孩子顶点可以不通过 \(u\) 而直接访问 \(u\) 的祖先顶点,那么此时去掉 \(u\) 是不会影响图的连通性的,所以 \(u\) 不是割点,相反,只要有一个孩子节点必须通过 \(u\) 才能访问 \(u\) 的祖先节点的话,那么现在的 \(u\) 就是一个割点。
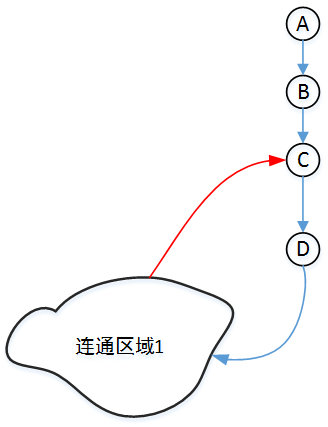
上面的图仅代表 DFS 时的顺序,并不代表是有向图。
对于顶点 \(D\) 而言,\(D\) 的孩子顶点可以通过联通区域 \(1\) 红色的部分的边回到 \(D\) 的祖先顶点 \(C\) (此时 \(c\) 已经被访问过了),所以 \(D\) 不是割点。
那么我们在代码里面该如何判断割点和桥呢?
割点:判断顶点 \(u\) 是否为割点,用 \(u\) 顶点的\(dfn\) 值和它的所有的孩子顶点的 \(low\) 值进行比较,如果存在至少一个孩子顶点 \(v\) 满足 \(low[v] >= dfn[u]\),就说明顶点 \(v\) 访问顶点 \(u\) 的祖先顶点,必须通过顶点 \(u\),而不存在顶点 \(v\) 到顶点 \(u\) 祖先顶点的其它路径,所以顶点 \(u\) 就是一个割点。对于没有孩子顶点的顶点,显然不会是割点。
桥(割边):\(low[v] > dfn[u]\) 就说明 \(V-U\) 是桥。

题目练习:
这是割点的板子题,所以很简单,具体注释看代码吧。
#include<bits/stdc++.h>
#define N 2000100
using namespace std;
struct sb{int u,v,next;}e[N];//存放输入的边
int head[N],low[N],dfn[N],vis[N];//low存放当前点所属的连通块,dfn存放时间戳,vis标记是否是割点
int n,m,tim,cnt,ans;
inline void add(int x,int y)//正常加边操作
{
e[++cnt].u=x;
e[cnt].v=y;
e[cnt].next=head[x];
head[x]=cnt;
}
void tajian(int x,int f)//tarjan算法主体
{
dfn[x]=low[x]=++tim;//赋初值
int c=0;
for(int i=head[x];i;i=e[i].next)//遍历每一个与之相连的点
{
int v=e[i].v;//取出终点
if(!dfn[v])//如果当前点没有被搜过
{
tajian(v,f);//继续往下搜
low[x]=min(low[x],low[v]);//当前带你所属的连通块的编号就是自己和孩子节点较小的那个
if(low[v]>=dfn[x]&&x!=f)//如果当前终点的low值大于dfn的x大小并且当前的点不是f
vis[x]=1;//当前点是割点
if(x==f)//如果当前的点就是一开始的祖先节点那就说明搜完一条边回来了,孩子节点加1
c++;//必须经过当前点才能访问祖先节点的孩子节点加一
}
low[x]=min(low[x],dfn[v]);//取当前点的连通块编号和孩子节点时间戳小的
}
if(c>=2&&x==f)//如果孩子个数大于2,并且当前点就是f
vis[x]=1;//标记是割点
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int x,y;
cin>>x>>y;
add(x,y);//无向图建边
add(y,x);
}
for(int i=1;i<=n;i++)
if(!dfn[i])//如果当前点没搜过
tajian(i,i);//开始搜
for(int i=1;i<=n;i++)
if(vis[i])//如果当前点是割点
ans++;//答案加1
cout<<ans<<endl;//输出
for(int i=1;i<=n;i++)
if(vis[i])
cout<<i<<" ";//按编号从小到大输出
return 0;//好习惯
}
给你一个图,问你去掉点 \(i\) 后满足 \((x,y)\) 不连通的数对的个数;
首先我们很容易就可以想到,可以分两种情况讨论,一种是当前点不是割点,当去掉与当前点相连的所有边之后图就分为了两部分,一部分是当前的单点,另一部分就是其余的点组成的联通块,所以此时的答案就是 \(2\times (n-1)\)。第二种情况就是当前点是割点,然后答案即为
\(a\) 是去掉边后图中连通块的数量,\(sum\) 是所有子树的点的个数和,\(t\) 存放每一个子树的大小,可以思考一下,割点的话,前面从 \(1\) 到 \(a\) 就是子树中的每一个点,和其他的点形成的数对,后面就是总的又算了一遍,因为数对里两个数的顺序是可以反着的。
code:
#include<bits/stdc++.h>
#define int long long
#define N 1001000
using namespace std;
struct sb{int u,v,next;}e[N];
int head[N],dfn[N],low[N],vis[N],siz[N];
int n,m,tot,cnt,ans[N];
inline void add(int u,int v)
{
e[++cnt].u=u;
e[cnt].v=v;
e[cnt].next=head[u];
head[u]=cnt;
}
void tarjan(int x,int f)
{
dfn[x]=low[x]=++tot;
siz[x]=1;
int ch=0,sum=0;
for(int i=head[x];i;i=e[i].next)
{
int v=e[i].v;
if(!dfn[v])
{
tarjan(v,f);
siz[x]+=siz[v];
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x])
{
ans[x]+=siz[v]*(n-siz[v]);
sum+=siz[v];
if(x==f)ch++;
if(x!=f||ch>1)vis[x]=1;
}
}
low[x]=min(low[x],dfn[v]);
}
if(!vis[x])ans[x]=2*(n-1);
else ans[x]+=(n-sum-1)*(sum+1)+(n-1);
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i,i);
for(int i=1;i<=n;i++)
cout<<ans[i]<<endl;
return 0;
}
本文来自博客园,作者:北烛青澜,转载请注明原文链接:https://www.cnblogs.com/Multitree/p/16683758.html
The heart is higher than the sky, and life is thinner than paper.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号