//https://img2018.cnblogs.com/blog/1646268/201908/1646268-20190806114008215-138720377.jpg

清北学堂题目整理

题单

Lazy Student

题目的意思就是给你一堆边权，然后给你每一条边是不是原图中最小生成树的树边，然后让你给出一个合理的构造。

首先我们按照边权的大小来排个序，然后从小到大进行连边，如果要是当前边的点和目标点没有连过边就连起来，这样可以保证每一个点的边都是最小生成树的树边，如果要是当前点已经练过了，我们就可以直接在之前已经连起来成一个强连通分量的点之间随便连，如果要是连满了就直接无解，退出即可，否则就可以构造出一组合法的解。

Long Jumps

我们考虑到，如果暴力枚举的话多半是会 T 的，所以我们想个办法优化

我们用 vis 数组来标记当前点往后的已经跳过了，因为序列里没有负值，所以当当前点的 vis 为 1 的时候，说明从当前点跳肯定不是最大的，因为有从前面的点跳过来的，这样前面的值肯定有比他大的。

等等老师讲的好像有问题

好像有可能会有不同的点跳到此点，然后直接退出是错的，所以我们再多维护一个 dis 表示从此点往后跳的最大值也就是记忆化搜索

不对我是sb

因为你要从后面过来的话，先遍历的过来跳的格肯定比后面跳过来的格多，得分更高，所以可以直接退出

Doremy's City Construction

我们考虑一下如何保证不会形成题目中的限制的图。

我们考虑按照点权把点分为两个部分，这样两个部分互相两两连边，就不会有影响了。为什么一定是分成两部分最优呢？你可以想一下，两个点的点权大小肯定是能比出来的，如果一个点 \(x\)，和一个点 \(y\)，建边 \(x\to y\)，\(y\) 的点权较大，如果此时向另外一个点连边，我们只能连向一个比 \(y\) 小的点，并且 \(x\) 与这个点不能直接相连，所以我们得出：图是一个二分图，而且在连边的时候，一个点 \(x\) 与比他大的点 \(y\) 相连后，就只能连向小于 \(y\) 的点了，同理，如果 \(x\) 比 \(y\) 大，\(y\) 就只能向比他大的点连边，所以我们排个序，然后根据乘法原理最大化连边即可。

Brain Network (medium)

求树的直径

Reposts

转化成数字跑一遍Floyd然后找出与自己相连的最大长度，然后直接加一输出即可

Party

因为不能有直接上司和自己在一起，所以就是找树上最长的链的长度

Masha and a Beautiful Tree

我们考虑将整个树上的点都看作一个序列，然后我们枚举 \(2^{i}\) 次方，枚举每一个合法的区间内两个区间的最后一位的值是否符合排完序的序列，然后如果不符合，就 \(cnt++\)，如果要是符合的话就直接跳过，最后到了枚举完的时候就直接输出答案即可。

Vertical Paths

我们可以从题目看出，一条路径只能向下走，也就是说，如果想要所有的点都走一遍的话，我们就必须把所有的叶子节点覆盖，也就是路径数等于叶子节点数。

那么我们就可以直接从每一个叶子节点往上搜，边搜边打标记，如果要是搜到了之前打过标记的点的话，我们就直接退出输出当前点的路径即可。

由于题目给出了每一个点的父节点，那么我们就可以把所有出现过的点标记为不是叶子节点，剩下的就都是叶子节点了。

点击查看代码 
#include<bits/stdc++.h>
#define endl '\n'
#define N 200100
using namespace std;
int t,n,ans,fa[N],stk[N],vis[N],ye[N];//ye是判断是否为叶子节点 
inline int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){f=ch!='-';ch=getchar();}while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return f?x:-x;}
signed main()
{
	t=read();
	while(t--)
	{
		n=read();
		for(int i=1;i<=n;i++)ye[i]=1,vis[i]=0;
		ans=0;
		for(int i=1;i<=n;i++)
		{
			fa[i]=read();
			if(fa[i]!=i)ye[fa[i]]=0;//父节点不是自己，说明当前的父节点肯定不是叶子节点 
		}
		for(int i=1;i<=n;i++)if(ye[i])ans++;//统计答案数 
		cout<<ans<<endl;
		for(int i=1;i<=n;i++)
        {
            if(ye[i])//遍历每一个点 
            {
                int now=i,len=0;//now是当前点的编号，len是路径长度 
                while(!vis[now])//只要当前点不空 
                {
                    stk[++len]=now;//存路径 
                    vis[now]=1;//标记遍历过
                    if(fa[now]==now)break;//如果到顶了就退出 
                    now=fa[now];//更新now 
                }
                cout<<len<<endl;//输出路径 
                for(int i=len;i>=1;i--)cout<<stk[i]<<" ";
                cout<<endl;
            }
        }
        cout<<endl;
	}
    return 0;
}

Bakery

给定 \(n\) 个点，从其中 \(k\) 个点中选一个点，从剩余的点中选一个点，使选出的两点距离最小。

我们思考一下，如果选出的两点要是中间会经过点的话，那么经过的这个点一定是属于两部分其中一部分的，我们可以把相应部分的那个选出来的点，改为中间经过的点，因为没有非正边权，所以这样一定会更优。

所以我们就可以枚举每一跳边，如果两端的点不同，我们就可以取个最小值，直接输出即可。

点击查看代码 
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define N 1000100
using namespace std;
int n,m,k,t[N],u[N],v[N],w[N],ans;
signed main()
{
    cin>>n>>m>>k;
    for(int i=1;i<=m;i++)cin>>u[i]>>v[i]>>w[i];
    for(int i=1;i<=k;i++){int x;cin>>x;t[x]=1;}//标记仓库 
    ans=INF;
    for(int i=1;i<=m;i++)if(t[u[i]]^t[v[i]])ans=min(ans,w[i]);//是一个面包店和一个仓库 
    if(ans==INF)cout<<"-1"<<endl;//无解 
    else cout<<ans<<endl;
    return 0;
}

The Door Problem

每个门只能用两个开关（钥匙）控制，明显的 2-SAT。

设当前开关为 \(i\) 表示使用，则 \(i+m\) 表示不使用此开关。

我们考虑建边，由于最后的门都是开的，并且我们知道开关按两次相当于不按，所以有以下两种情况：

  1. 当前门是关着的，所以需要开奇数次的开关，所以两个开关的次数分别为一奇一偶，而由上面得知偶数的相当于不开，所以相当于其中一个开关只能开一次，所以设控制当前门的开关为 \((i,j)\)，所以链接 \((i,j+m),(i+m,j),(j+m,i),(j,i+m)\)。

  2. 当前门是开着的，所以需要开偶数次的开关，同上可以想出两个开关要么都开一次，要么都不开，设控制当前门的开关为 \((i,j)\)，所以链接 \((i,j),(j,i),(i+m,j+m),(j+m,i+m)\)。

然后我们的图建好了，跑一遍 2-SAT 模板就好了。

点击查看代码 
#include<bits/stdc++.h>
#define N 1000100
using namespace std;
struct sb{int u,v,next;}e[N];
int n,m,cnt,a[N],mp[N][2],low[N],dfn[N],tim,stk[N],top,vis[N],sd[N],head[N];//加n表示不用 
inline int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){f=ch!='-';ch=getchar();}while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return f?x:-x;}
inline void add(int u,int v){e[++cnt].v=v;e[cnt].next=head[u];head[u]=cnt;}
inline void tarjan(int x)
{
	low[x]=dfn[x]=++tim;vis[x]=1,stk[++top]=x;
	for(int i=head[x];i;i=e[i].next)
	{
		int v=e[i].v;
		if(!dfn[v])tarjan(v),low[x]=min(low[x],low[v]);
		else if(vis[v])low[x]=min(low[x],dfn[v]);
	}
	if(low[x]==dfn[x])
	{
		int y;
		while(1)
		{
			y=stk[top--];
			sd[y]=x;
			vis[y]=0;
			if(x==y)break;
		}
	}
}
signed main()
{
	n=read();m=read();
	for(int i=1;i<=n;i++)a[i]=read();
	for(int i=1;i<=m;i++)
	{
		int k=read();
		for(int j=1;j<=k;j++)
		{
			int x=read();
			if(!mp[x][0])mp[x][0]=i;
			else mp[x][1]=i;
		}
	}
	for(int i=1;i<=n;i++)
	{
		if(a[i]==0)
		{
			add(mp[i][0],mp[i][1]+m);
			add(mp[i][1],mp[i][0]+m);
			add(mp[i][0]+m,mp[i][1]);
			add(mp[i][1]+m,mp[i][0]);
		}
		else 
		{
			add(mp[i][0],mp[i][1]);
			add(mp[i][1],mp[i][0]);
			add(mp[i][0]+m,mp[i][1]+m);
			add(mp[i][1]+m,mp[i][0]+m);
		}
	}
	for(int i=1;i<=m*2;i++)if(!dfn[i])tarjan(i);
	for(int i=1;i<=m;i++)
	{
		if(sd[i]==sd[i+m])
		{
			cout<<"NO"<<endl;
			return 0;
		}	
	}
	cout<<"YES"<<endl;
	return 0;
}

Unusual Matrix

发现从 A 矩阵到 B 矩阵的步骤，就相当于把 A 和 B 两个矩阵对应的两个数异或起来得到的新矩阵全变成 \(0\)。

因为要把 A 变成 B，此时 A 和 B 对应的两个数异或起来得到的数全是 \(0\)，所以可以把未改变的两个矩阵对应的两个数异或得到的新矩阵全通过行列变化成为 \(0\)，也就相当于使 A 矩阵变化成 B 矩阵了。

我们得到新矩阵后目标是全变成 \(0\)，而异或一个数偶数次就相当于没有异或，奇数次就相当于只异或一次，所以我们考虑 2-SAT。

我们设 \(i\) 表示第 \(i\) 行进行变化，\(i+n\) 表示第 \(i\) 列变化，\(i+2n\) 表示第 \(i\) 行不变化，\(i+3n\) 表示第 \(i\) 列不变化。

  1. 如果新矩阵当前点是 \(0\) 说明不需要异或，只能行列都变化或者都不变化，所以连 \(i\to j+n,j+n\to i,i+2n\to j+3n,j+3n\to i+2n\)。

  2. 如果新矩阵当前点是 \(1\) 说明行列只能变化一个，所以连 \(i\to j+3n,j+3n\to i,i+2n\to j+n,j+n\to i+2n\)。

然后跑一遍 tarjan 判一下是否有解输出即可。

点击查看代码 
#include<bits/stdc++.h>
#define N 4000100
#define M 1100 
#define endl '\n' 
using namespace std;
string a[M],b[M];
struct sb{int u,v,next;}e[N];
int n,t,low[N],dfn[N],tim,sd[N],vis[N],cnt,head[N],stk[N],top,flag;
inline void add(int u,int v){e[++cnt].v=v;e[cnt].next=head[u];head[u]=cnt;} 
inline void qk(){flag=cnt=tim=0;for(int i=1;i<=4*n;i++)head[i]=low[i]=dfn[i]=vis[i]=sd[i]=0;}
inline void tarjan(int x)
{
	low[x]=dfn[x]=++tim;vis[x]=1;stk[++top]=x;
	for(int i=head[x];i;i=e[i].next)
	{
		int v=e[i].v;
		if(!dfn[v])tarjan(v),low[x]=min(low[x],low[v]);
		else if(vis[v])low[x]=min(low[x],dfn[v]);
	}
	if(dfn[x]==low[x])
	{
		int y;
		while(1)
		{
			y=stk[top--];
			sd[y]=x;
			vis[y]=0;
			if(x==y)break;
		}
	}
}
signed main()
{
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		qk();
		for(int i=1;i<=n;i++)cin>>a[i];
		for(int i=1;i<=n;i++)cin>>b[i];
		for(int i=1;i<=n;i++)
		{
		    for(int j=1;j<=n;j++)
		    {
		    	int c=(a[i][j-1]-'0')^(b[i][j-1]-'0');
		    	if(c==1)
		    	{
		    		add(i,j+3*n);//i行^,i+2n行不^,j+n列^,j+3n不^ 
		    		add(j+3*n,i);
		    		add(i+2*n,j+n);
		    		add(j+n,i+2*n);
				}
				else 
				{
					add(i,j+n);
					add(j+n,i);
					add(i+2*n,j+3*n);
					add(j+3*n,i+2*n);
				}
		    }
		}
		for(int i=1;i<=4*n;i++)if(!dfn[i])tarjan(i);
		for(int i=1;i<=2*n;i++)if(sd[i]==sd[i+2*n]){flag=1;break;}
		if(flag)cout<<"NO"<<endl;
		else cout<<"YES"<<endl;
	}
	return 0;
}

Shichikuji and Power Grid

我们很容易想到建一个超级源点向每一个点连边，边权为建发电站的费用，这样就处理了在点建发电站的问题。

然后我们枚举两个点直接建边跑克鲁斯卡尔，但是由于图太稠密了，所以我们复杂度并不理想，观察题面说输出的边是任意顺序，所以只建一条边即可，然后就能过了。

点击查看代码 
#include<bits/stdc++.h>
#define int long long
#define N 100100
#define endl '\n'
#define parii pair<int,int>
using namespace std;
queue<int>q;
queue<parii>q1;
int n,a[N],k[N],X[N],Y[N],cnt,head[N],num,ans,f[N],cao;
struct sb{int u,v,next,w;}e[N<<5];
inline int cmp(sb a,sb b){return a.w<b.w;}
inline int fid(int x){if(f[x]==x)return x;return f[x]=fid(f[x]);}
inline void add(int u,int v,int w){e[++cnt].v=v;e[cnt].u=u;e[cnt].w=w;e[cnt].next=head[u];head[u]=cnt;}
inline int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){f=ch!='-';ch=getchar();}while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return f?x:-x;}
signed main()
{
	n=read();
	for(int i=1;i<=n+1;i++)f[i]=i;
	for(int i=1;i<=n;i++)X[i]=read(),Y[i]=read();
	for(int i=1;i<=n;i++)a[i]=read();
	for(int i=1;i<=n;i++)k[i]=read();
	for(int i=1;i<=n;i++)add(n+1,i,a[i]);
//	,add(i,n+1,a[i]);
	for(int i=1;i<=n;i++)
	  for(int j=i+1;j<=n;j++)
	    add(i,j,(k[i]+k[j])*(abs(X[i]-X[j])+abs(Y[i]-Y[j])));
//	    add(j,i,(k[i]+k[j])*(abs(X[i]-X[j])+abs(Y[i]-Y[j])));
//		cout<<"jl:"<<(k[i]+k[j])*(abs(X[i]-X[j])+abs(Y[i]-Y[j]))<<endl;
	sort(e+1,e+cnt+1,cmp);
	for(int i=1;i<=cnt;i++)
	{
		int xx=fid(e[i].u);
		int yy=fid(e[i].v);
		if(xx==yy)continue;
//		cout<<"xx:"<<xx<<"  yy:"<<yy<<endl;
		f[xx]=yy;
		if(e[i].u==n+1||e[i].v==n+1)cao++,q.push((e[i].u==n+1?e[i].v:e[i].u));
		else q1.push({e[i].u,e[i].v});
		ans+=e[i].w;
		num++;
		if(num==n)break;
	}
	cout<<ans<<endl;
	cout<<cao<<endl;
	while(!q.empty()){cout<<q.front()<<" ";q.pop();}
	cout<<endl<<(num-cao)<<endl;
	while(!q1.empty()){cout<<q1.front().first<<" "<<q1.front().second<<endl;q1.pop();}
	return 0;
}

Johnny Solving

Q1

我们分析一下两个问题就会发现第一问是比较好判断的，因为如果我们用 DFS 求一棵生成树，看一下直径是否 \(\ge \frac{n}{k}\) 就好了。

Q2

第一问，如果不成立，那就说明直径是小于 \(\frac{n}{k}\) 的，同理可以推出树的最大深度也是小于 \(\frac{n}{k}\) 的，而题目说了保证每个点的度数大于等于 \(3\)，这样你是构造不出叶子节点小于 \(k\) 的树的，因为如果要没有 \(\ge \frac{n}{k}\) 的链的话，链最长为 \(\frac{n}{k}-1=\frac{n-k}{k}\)，那么最优的构造就是菊花图。

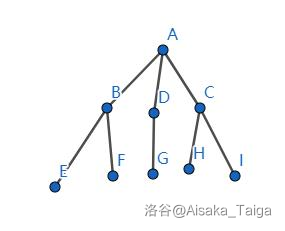
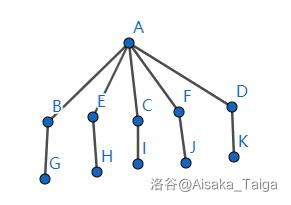
显然第二种更优，因为同样的叶子节点数包含了更多的点。

所以链数 \(=\) 叶子节点数 \(=n\times \frac{k}{n-k}=\frac{n\times k}{n-k}\)，因为 \(n\ge k\) 所以 \(n\times k\ge k^{2}\)，\(n\) 一定是大于 \(n-k\) 的，将 \(\frac{n}{n-k}\) 看作一个已知数的话一定是恒大于 \(1\) 的，所以这个式子的值一定是恒大于 \(k\) 的，但由于是向下取整所以是有可能等于 \(k\) 的，所以叶子节点数肯定是 \(\ge k\) 的。

题目中说保证每个点度数大于等于 \(3\)，那么叶子节点肯定就只能是和自己上面的点连，也就是返祖边，因为没有重边所以一定有两条连在父亲节点往上的点的边，那么一定有一个环是大于 \(3\) 的。也许你会问为什么一定是返祖边而不是横叉边，因为我们是按 DFS 序找的生成树，假如我们最后得到的生成树是下面的模样：

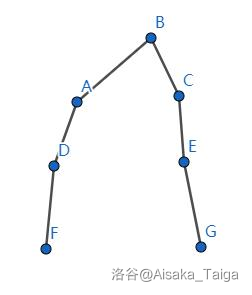
如果要是 \(F\to E\) 有边，那么我们在 DFS 的时候 \(E\) 会成为 \(F\) 的子节点，也就是说在这个 DFS 生成树上是不存在横叉边的，是 DFS 序保证了剩余的两条边都是返祖边。

所以我们这样就一定至少能找出 \(k\) 个环了，但是如何处理对于环的限制？

对于至少一个点在 \(k\) 个环里只出现一次，我们只要对于每一个叶子节点都只计算一个环就好了，这样每一个叶子节点都是只出现了一次。

对于环的长度 \(len>3\) 且 \(len\bmod3 \ne 0\)，我们可以想一下，设 \(dep_{i}\) 表示 \(i\) 号点在生成树上的深度。

我们画个图就可以知道：

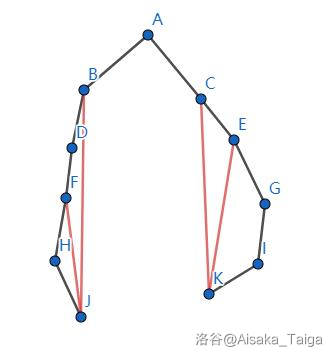
上图中以 \(J\) 为叶子节点讨论有三个环：

  1. \(J,H,F\) 构成的环，长度为 \(dep_{J}-dep_{F}+1\)。

  2. \(J,H,F,D,B\) 构成的环，长度为 \(dep_{J}-dep_{B}+1\)。

  3. \(J,F,D,B\) 构成的环，长度为 \(dep_{F}-dep_{B}+2\)。

那么万一里面没有符合条件的环呢？

设当前点为 \(u\)，返祖边连向的祖先为 \(x,y\)。

如果 \(dep_{u}-dep_{x}+1\) 和 \(dep_{u}-dep_{y}+1\) 都为 \(3\) 的倍数，那么两个式子做差可以得到 \(dep_{x}-dep_{y}\) 为 \(3\) 的倍数，那么加上 \(2\) 肯定就不是 \(3\) 的倍数了，其他两种情况也是这样，可以得出每一个叶子节点必定有一个环符合要求。

上面的推理都是基于生成树上的点的最大深度 \(< \frac{n}{k}\) 的，所以也就是说只要生成树上的点的最大深度小于 \(\frac{n}{k}\) 第二问就有解，所以我们可以不用求树的直径，直接在 DFS 的时候顺便处理每一个点的深度就好，最后用这个值来判断做第一问还是第二问。

点击查看代码 
#include<bits/stdc++.h>
#define N 1000100
#define M 250010
#define endl '\n'
using namespace std;
int n,m,k,cnt,head[N],cl,ye[M],dep[M],fa[M],zx[M][2],mxdep,ed;
struct sb{int u,v,next;}e[N];
inline void add(int u,int v){e[++cnt].v=v;e[cnt].next=head[u];head[u]=cnt;}
inline int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){f=ch!='-';ch=getchar();}while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return f?x:-x;}
inline void print(int u,int v){cout<<v<<" ";if(u==v)return ;print(u,fa[v]);}
inline void dfs(int u,int f,int dp)
{
	dep[u]=dp;
	if(dep[u]>mxdep)mxdep=dep[u],ed=u;
	fa[u]=f;
	ye[++cl]=u;
	for(int i=head[u];~i;i=e[i].next)
	{
		int v=e[i].v;
		if(v==f)continue;
		if(dep[v]){if(!zx[u][0])zx[u][0]=v;else zx[u][1]=v;continue;}
		if(ye[cl]==u)cl--;
		dfs(v,u,dp+1);
	}
}
signed main()
{
	memset(head,-1,sizeof head);
	n=read(),m=read(),k=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read();
		add(u,v),add(v,u);
	}
	dfs(1,-1,1);
	if(mxdep>=n/k)
	{
		cout<<"PATH"<<endl<<mxdep<<endl;
		while(ed!=-1)cout<<ed<<" ",ed=fa[ed];
		return 0;
	}
	cout<<"CYCLES"<<endl;
	for(int i=1;i<=k;i++)
	{
		int u=ye[i],x=zx[u][0],y=zx[u][1];
		if(dep[x]>dep[y])swap(x,y);
		if((dep[u]-dep[x]+1)%3!=0)//u和x构成环 
		{
			cout<<(dep[u]-dep[x]+1)<<endl;
			print(x,u);cout<<endl;
		}
		else if((dep[u]-dep[y]+1)%3!=0)//u和y构成环 
		{
			cout<<(dep[u]-dep[y]+1)<<endl;
			print(y,u);cout<<endl;
		}
		else//x和y构成环 
		{
			cout<<(dep[y]-dep[x]+2)<<endl<<u<<" ";
			print(x,y);cout<<endl;
		}
	}
	return 0;
}
posted @ 2023-05-03 19:10  北烛青澜  阅读(13)  评论(0)  编辑  收藏  举报