斐波那契数列问题
菲波那切数列问题
1,概述
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果
LeetCode-509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
2,解决思路
2.1,暴力递归
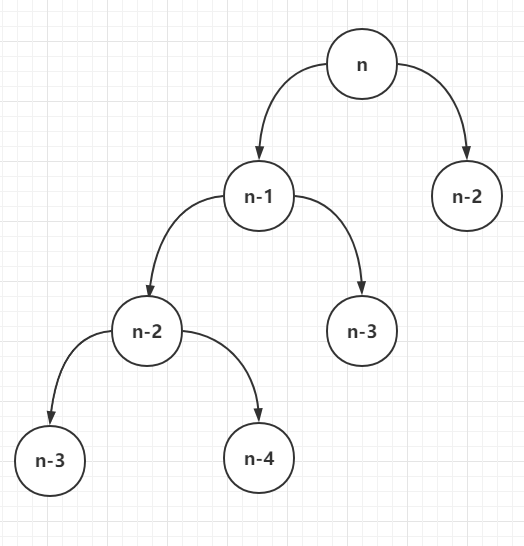
直接使用递归,由计算F(n)结果,转变为计算F(n-1)和F(n-2)的结果,然后逐次递归计算
缺点是会有很多重复计算,例如N=10,那么F(3)会额外重复计算很多次
// 1,暴力递归求解
public int fib(int n) {
if (n <= 1) {
return n;
}
return fib(n - 1) + fib(n - 2);
}
/*
结果:102334155
耗时:534
*/
时间复杂度
原因:
①这种递归类似于二叉树,最底层的是2N个计算节点,时间复杂度O(2N)
空间复杂度
原因:
①考虑栈(stack)内存耗费情况下,该计算逻辑类似一个非平衡的二叉树,偏向左节点,需要2N个栈空间进行存储,空间复杂度O(2N)
②如果不考虑栈(stack)内存耗费,那么空间复杂度为O(1),不需要额外的数据存储空间
从我自己感知的空间复杂度计算上来说,栈空间一般是不考虑在内的
2.2,缓存计算结果
在参考上述暴力递归解法的重复计算问题,这里使用hashMap将已经计算过的F(N)结果进行缓存,然后将在需要使用的时候进行提取
// 2,缓存历史计算结果
private HashMap<Integer,Integer> cache = new HashMap<>();
public Solution1() {
cache.put(0,0);
cache.put(1,1);
}
public int fib2(int n) {
if(cache.containsKey(n)){
return cache.get(n);
}
cache.put(n,fib2(n - 1) + fib2(n - 2));
return cache.get(n);
}
/*
结果:102334155
耗时:1
*/
时间复杂度
O(N)
原因:只用计算一遍即可,消除很多次重复计算
空间复杂度
O(N)
原因:需要额外的数据存空间用于缓存历史计算结果
2.3,模拟法
直接模拟计算的过程,类似于将从头开始计算到最终的N值
// 3,模拟法
public int fib3(int n) {
if (n <= 1) {
return n;
}
int n0 = 0, n1 = 1;
for (int i = 2; i <= n; i++) {
if (i % 2 == 0) {
n0 += n1;
} else {
n1 += n0;
}
}
if (n % 2 == 0) {
return n0;
} else {
return n1;
}
}
/*
结果:102334155
耗时:1
*/
时间复杂度
O(N)
原因:只用计算一遍即可,消除很多次重复计算
空间复杂度
O(1)
原因:无需额外的栈空间和数据存储空间
2.4,思路对比
| 思路 | 时间复杂度 | 空间复杂度 | 评价 |
|---|---|---|---|
| 暴力递归 | 2^N | N,栈空间 | 时间复杂度最高,效率低 |
| 缓存历史计算结果 | N | N,数据存储空间 | 空间复杂度高 |
| 模拟法 | N | 1 | 时间和空间复杂度最低 |
3,样例
LeetCode-70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
这个问题,本质就是斐波那契数列问题

// 3,模拟法:
public int climbStairs(int n) {
if (n <= 2) {
return n;
}
int n1 = 1, n2 = 2;
for (int i = 3; i <= n; i++) {
if (i % 2 == 1) {
n1 += n2;
} else {
n2 += n1;
}
}
return n % 2 == 1 ? n1 : n2;
}
其他的斐波那契数列问题,例如兔子繁殖等等,基本上都是按照上述解决思路进行解决的


