滤波器算法（1）-卡尔曼滤波小车附带题目与MATLAB程序
1 简介
由卡尔曼这个学者提出的最佳线性滤波器，单纯时域维度即可实现【无需进行频域变换】
2 思路
由上一时刻的最佳估计值XKE_P预测①当前时刻预测值Pxv 与 ②当前时刻的测量值Mxv 进行联立计算获得当 ③前时刻的最佳估计值XKE
3 核心
4 Matlab实例
4.1 题目【老师留的课堂作业】
研一的时候做过一次，当时没有总结；最近师弟们在写这个作业花时间重新弄了一遍，做了一次总结
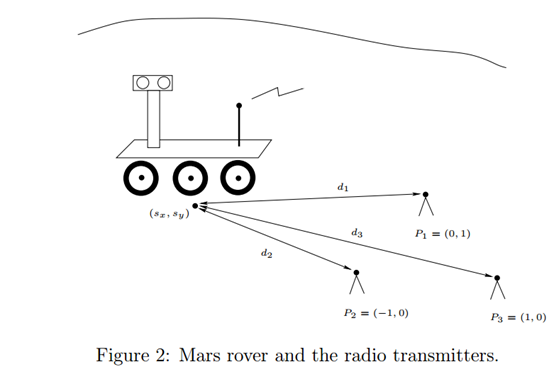
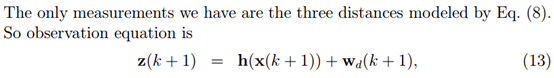
4.2 源代码
不带BU参数
version9_release.m
%% 卡尔曼滤波的发布版本程序
%% 时间：2019.12.05
%% 版本：v9
%% 特性：单参处理【防止多维度计算混乱】
%% TODO：引入多参数进一步优化算法
%% 数据读取
% MDistance=importdata('RoverMeasurementData.txt');
Mxv=importdata('data3.mat'); % 笛卡尔坐标系，测量值
Txv=importdata('RoverTrueStates.txt'); % 真实值
len=size(Mxv,1);
%% 参数设置
q=0.010000 ; R=0.500000;
Q=[1 0;0 1].*q;
%% 正式处理
XKE=zeros(4,len);
for i=1:len
xv = func_kalmanFilter_singleVal(Mxv(i,1),Q,R,i);
XKE(1,i)=xv(1);
XKE(3,i)=xv(2);
end
for i=1:len
xv = func_kalmanFilter_singleVal(Mxv(i,2),Q,R,i);
XKE(2,i)=xv(1);
XKE(4,i)=xv(2);
end
%% 图谱显示
figure(1);
plot(Txv(1,:),Txv(2,:),'r-*','markersize',8),hold on;
plot(XKE(1,:),XKE(2,:),'b-s','markersize',8),hold on;
plot(Mxv(:,1),Mxv(:,2),'g-v','markersize',8),hold on;
xlabel('位置x');
ylabel('位置y');
legend({'真实值','估计值','测量值'},'Location','northwest');%
set(gca,'FontSize',25);
figure(2);
sub_XKE=sqrt((XKE(1,:)-Txv(1,:)).^2+(XKE(2,:)-Txv(2,:)).^2);
sub_Mxv=sqrt((Mxv(:,1)'-Txv(1,:)).^2+(Mxv(:,2)'-Txv(2,:)).^2);
plot(sub_XKE,'b-s','markersize',8),hold on;
plot(sub_Mxv,'g-v','markersize',8),hold on;
xlabel('时间t');
ylabel('与真实值的距离均方差d');
legend({'估计值误差','测量值误差'},'Location','northwest');%
set(gca,'FontSize',25);
% print -djpeg -r600 不带BU位置点;
% print -djpeg -r600 不带BU方差值;
version10_release.m
%% 卡尔曼滤波的发布版本程序
%% 时间：2019.12.05
%% 版本：v9
%% 特性：单参处理【防止多维度计算混乱】
%% TODO：引入多参数进一步优化算法
%% 数据读取
% MDistance=importdata('RoverMeasurementData.txt');
Mxv=importdata('data3.mat'); % 笛卡尔坐标系，测量值
Txv=importdata('RoverTrueStates.txt'); % 真实值
%% 参数设置
MCN=20;
d_range1=0.01;
d_range2=0.01;
q=0:d_range1:1;
R=0:d_range2:0.5;
len1=size(q,2);
len2=size(R,2);
Q=[1 0;0 1];
%% 正式处理
sub_map=zeros(1,len1*len2);
len=len1*len2;
tic;
t1=toc;
% for k=1:len
parfor k=1:len
i=mod(k-1,len1)+1; %行号
j=floor((k-1)/len1)+1; %列号
sub_map(k)=func_kalmanFilter_doubleVal(Mxv,Txv, Q.*q(1,i), R(1,j), MCN);
fprintf('run is going on k=%d,index=(%d, %d)\n',k,i,j);
end
t2=toc;
fprintf('耗时t=%f\n',(t2-t1));
%% 获取当前最优解
sub_min=min(sub_map);
k=find(sub_map==sub_min);
i=mod(k-1,len1)+1; %行号
j=floor((k-1)/len1)+1; %列号
Eq=q(1,i);
ER=R(1,j);
fprintf('当前最优解 q=%f ; R=%f ,sub=%f\n',Eq,ER,sub_min);
%% 显示图谱
sub_map=reshape(sub_map,len1,len2);
[X,Y]= meshgrid(q,R);
figure(1);
mesh(X',Y',sub_map);
xlabel('Q预测模型噪声');
ylabel('R观测噪声');
%% 最优数值解1
% q=0.017;
% R=3.6;
% sub=32.0530;
% 当前最优解 q=0.010000 ; R=0.500000 ,sub=44.573339
带BU参数
version11_release.m
%% 卡尔曼滤波的发布版本程序
%% 时间：2019.12.05
%% 版本：v11
%% 特性：引入加速度参与计算
%% TODO：引入多参数进一步优化算法
%% 数据读取
% MDistance=importdata('RoverMeasurementData.txt');
Mxv=importdata('data3.mat'); % 笛卡尔坐标系，测量值
Txv=importdata('RoverTrueStates.txt'); % 真实值
len=size(Mxv,1);
%% 参数设置
% q=0.006000;
% R=1.270000 ;
% q=0.006000 ; R=0.010000 ;
% q=0.030000 ; R=0.050000 ;
% q=0.030000 ; R=0.050000;
q=0.040000 ; R=0.050000;
Q=[1 0;0 1].*q;
%% 正式处理
XKE=zeros(4,len);
for i=1:len
xv = func_kalmanFilter_singleVal_withBU(Mxv(i,1),Q,R,i);
XKE(1,i)=xv(1);
XKE(3,i)=xv(2);
end
for i=1:len
xv = func_kalmanFilter_singleVal_withBU(Mxv(i,2),Q,R,i);
XKE(2,i)=xv(1);
XKE(4,i)=xv(2);
end
%% 图谱显示
figure(1);
plot(Txv(1,:),Txv(2,:),'r-*','markersize',8),hold on;
plot(XKE(1,:),XKE(2,:),'b-s','markersize',8),hold on;
plot(Mxv(:,1),Mxv(:,2),'g-v','markersize',8),hold on;
xlabel('位置x');
ylabel('位置y');
legend({'真实值','估计值','测量值'},'Location','northwest');%
set(gca,'FontSize',25);
figure(2);
sub_XKE=sqrt((XKE(1,:)-Txv(1,:)).^2+(XKE(2,:)-Txv(2,:)).^2);
sub_Mxv=sqrt((Mxv(:,1)'-Txv(1,:)).^2+(Mxv(:,2)'-Txv(2,:)).^2);
plot(sub_XKE,'b-s','markersize',8),hold on;
plot(sub_Mxv,'g-v','markersize',8),hold on;
xlabel('时间t');
ylabel('与真实值的距离均方差d');
legend({'估计值误差','测量值误差'},'Location','northwest');%
set(gca,'FontSize',25);
% print -djpeg -r600 带BU位置点;
% print -djpeg -r600 带BU方差值;
version12_release.m
%% 卡尔曼滤波的发布版本程序
%% 时间：2019.12.05
%% 版本：v9
%% 特性：单参处理【防止多维度计算混乱】
%% TODO：引入多参数进一步优化算法
%% 数据读取
% MDistance=importdata('RoverMeasurementData.txt');
Mxv=importdata('data3.mat'); % 笛卡尔坐标系，测量值
Txv=importdata('RoverTrueStates.txt'); % 真实值
%% 参数设置
MCN=20;
d_range1=0.01;
d_range2=0.01;
q=0:d_range1:1;
R=0:d_range2:0.5;
len1=size(q,2);
len2=size(R,2);
Q=[1 0;0 1];
%% 正式处理
sub_map=zeros(1,len1*len2);
len=len1*len2;
tic;
t1=toc;
% for k=1:len
parfor k=1:len
i=mod(k-1,len1)+1; %行号
j=floor((k-1)/len1)+1; %列号
sub_map(k)=func_kalmanFilter_doubleVal_withBU(Mxv,Txv, Q.*q(1,i), R(1,j), MCN);
fprintf('run is going on k=%d,index=(%d, %d)\n',k,i,j);
end
t2=toc;
fprintf('耗时t=%f\n',(t2-t1));
%% 获取当前最优解
sub_min=min(sub_map);
k=find(sub_map==sub_min);
i=mod(k-1,len1)+1; %行号
j=floor((k-1)/len1)+1; %列号
Eq=q(1,i);
ER=R(1,j);
fprintf('当前最优解 q=%f ; R=%f ,sub=%f\n',Eq,ER,sub_min);
%% 显示图谱
sub_map=reshape(sub_map,len1,len2);
[X,Y]= meshgrid(q,R);
figure(1);
mesh(X',Y',sub_map);
xlabel('Q预测模型噪声');
ylabel('R观测噪声');
%% 最优数值解1
% q=0.017;
% R=3.6;
% sub=32.0530;
% 当前最优解 q=0.040000 ; R=0.050000 ,sub=57.511923
func_kalmanFilter_doubleVal
%% 参数比较数据Q、R的数据比较
function [sub_mean] = func_kalmanFilter_doubleVal(Mxv,Txv, Q, R, MCN)
sub_cell=zeros(1,MCN);
len=size(Mxv,1);
XKE=zeros(4,len);
for iRun=1:MCN
%% 处理数据
for i=1:len
xv = func_kalmanFilter_singleVal(Mxv(i,1),Q,R,i);
XKE(1,i)=xv(1);
XKE(3,i)=xv(2);
end
for i=1:len
xv = func_kalmanFilter_singleVal(Mxv(i,2),Q,R,i);
XKE(2,i)=xv(1);
XKE(4,i)=xv(2);
end
%% 计算均方差和
sub=sqrt((XKE(1,end-50:end)-Txv(1,end-50:end)).^2+(XKE(2,end-50:end)-Txv(2,end-50:end)).^2);
sub_cell(1,iRun)=sum(sub);
end
sub_mean=mean(sub_cell);
end
func_kalmanFilter_singleVal
%% 单参卡尔曼滤波函数
function [XKE] = func_kalmanFilter_singleVal(Z,Q,R,iLoop)
%FUNC_KALMANFILTER_ 此处显示有关此函数的摘要
% 此处显示详细说明
persistent X;
persistent P;
persistent F;
persistent H;
if iLoop==1
X=[0;0];
P=[1 0;0 1];
F=[1 1;0 1];
H=[1 0];
end
X_=F*X;
P_=F*P*F'+Q;
K=P_*H'/(H*P_*H'+R);
X=X_+K*(Z-H*X_);
P=(eye(2)-K*H)*P_;
XKE=X;
end
func_kalmanFilter_doubleVal_withBU
%% 参数比较数据Q、R的数据比较
function [sub_mean] = func_kalmanFilter_doubleVal_withBU(Mxv,Txv, Q, R, MCN)
sub_cell=zeros(1,MCN);
len=size(Mxv,1);
XKE=zeros(4,len);
for iRun=1:MCN
%% 处理数据
for i=1:len
xv = func_kalmanFilter_singleVal_withBU(Mxv(i,1),Q,R,i);
XKE(1,i)=xv(1);
XKE(3,i)=xv(2);
end
for i=1:len
xv = func_kalmanFilter_singleVal_withBU(Mxv(i,2),Q,R,i);
XKE(2,i)=xv(1);
XKE(4,i)=xv(2);
end
%% 计算均方差和
sub=sqrt((XKE(1,end-50:end)-Txv(1,end-50:end)).^2+(XKE(2,end-50:end)-Txv(2,end-50:end)).^2);
sub_cell(1,iRun)=sum(sub);
end
sub_mean=mean(sub_cell);
end
func_kalmanFilter_singleVal_withBU
%% 带加速度参数的卡尔曼滤波器
function [XKE] = func_kalmanFilter_singleVal_withBU(Z,Q,R,iLoop)
%FUNC_KALMANFILTER_SINGLEVAL_WITHBU 此处显示有关此函数的摘要
% 此处显示详细说明
persistent X; % 位置与速度
persistent U; % 加速度
persistent P; % 协方差矩阵
persistent F; % 状态转移矩阵
persistent B; % 状态控制矩阵
persistent H; % 观测矩阵
if iLoop==1
X=[0;0];
U=0;
P=[1 0;0 1];
F=[1 1;0 1];
B=[1./2;1];
H=[1 0];
end
X_=F*X+B*U; % ① 状态预测公式
P_=F*P*F'+Q; % ② 噪声协方差传递
K=P_*H'/(H*P_*H'+R); % ③ 卡尔曼系数计算
XK=X;%暂存前一时刻数据
X=X_+K*(Z-H*X_); % ④ 计算最优估计值
P=(eye(2)-K*H)*P_; % ⑤ 噪声协方差矩阵更新
U=X(2,1)-XK(2,1);
XKE=X;
end
4.3 结果显示
不带控制参数的位置点数据图谱：
不带控制参数的方差值图谱：
带控制参数的位置点数据图谱：
带控制参数的方差值图谱：
5 总结
性能确实还可以的，里面的难点在于各个矩阵运算以及Q、R参数的设定，这里我是使用随机参数法，广撒网多次蒙特卡洛仿真求均值，最后在这些参数中选择最优的那个解为我的模型参数。
6 相关链接
开源代码：
链接：https://pan.baidu.com/s/1fUM0VmPVabqKv89WUyZmng 提取码：x3zv
参考链接：
探究未知是最大乐趣
