奇妙的算法【7】-贪婪算法-dp

问题1描述：【贪婪算法，Dijistra算法】

①有一只兔子要从一个N*N的二维矩阵方格中从上跳到下面；

②每次只能向左或向下，越过一个方格，跳到下一个方格中；

③被越过的方格中的数值，表示该兔子越过该方格后需要休息的时间（或者能量）;

求：到达最下面方格花费的最少时间是多少？

输入：

第一行，输入一个数值N

后面输入N行，每行有N个数值并且由【,】隔开

输出：

输出一个数据M,M为兔子需要花费的最小时间

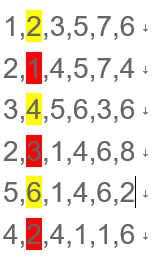
示例：
输入：
6
1,2,3,5,7,6
2,1,4,5,7,4
3,4,5,6,3,6
2,3,1,4,6,8
5,6,1,4,6,2
4,2,4,1,1,6
输出：
6

   

 

算法1【递归调用】：以后不考虑这种算法

注意：这种方法虽然可以结题，但是如果数据量太大，时间上耗时太多了，每次都不能全部AC，这次只能AC40%

package com.cnblogs.mufasa.demo1;

import java.util.Scanner;

class Answer1_1 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        String line = scanner.nextLine();
        int n = Integer.parseInt(line);
        int[][] area = new int[n][n];

        for (int i = 0; i < n; i++) {
            line = scanner.nextLine();
            String[] split = line.split(",");
            if (split.length != n) {
                throw new IllegalArgumentException("错误输入");
            }
            int j = 0;
            for (String num : split) {
                area[i][j++] = Integer.parseInt(num);
            }
        }

        int minimumTimeCost = getMinimumTimeCost(n,area);
        System.out.println(minimumTimeCost);
    }

    /** 请完成下面这个函数，实现题目要求的功能 **/
    /** 当然，你也可以不按照这个模板来作答，完全按照自己的想法来 ^-^  **/
    private static int getMinimumTimeCost(int n, int[][] area) {
        long startTime =  System.currentTimeMillis();
        int[] nums=new int[n];
        for(int i=0;i<n;i++){
            nums[i]=getMinSingleLine(n,area,0,i,0);
        }
        int min=nums[0];
        for(int i=1;i<n;i++){
            if(min>nums[i]){
                min=nums[i];
            }
        }
        long endTime =  System.currentTimeMillis();
        System.out.println(endTime-startTime);
        return min;
    }

    private static int getMinSingleLine(int n,int[][] area,int index0,int index1,int times ){
        if(index0==n-2&&(index1==n-1||index1==n-2)){//1，极限位置,正确
            return times+area[index0+1][index1];
        }else if(index1==n-1||index1==n-2){//2，只能往下走，正确
            return getMinSingleLine(n,area,index0+2,index1,times+area[index0+1][index1]);
        }else if(index0==n-2){//3，向下一步或向右，正确
            return Math.min(times+area[index0+1][index1],getMinSingleLine(n,area,index0,index1+2,times+area[index0][index1+1]));
        }else{
            return Math.min(getMinSingleLine(n,area,index0+2,index1,times+area[index0+1][index1]),getMinSingleLine(n,area,index0,index1+2,times+area[index0][index1+1]));
        }
    }
}
/*
8
35,92,98,68,35,65,26,72
29,78,83,16,5,89,92,28
48,51,37,79,65,74,50,71
98,78,99,57,1,30,22,16
72,88,55,33,56,58,28,49
4,28,29,20,18,61,11,73
61,19,47,34,85,32,77,89
29,49,10,81,52,5,63,25
 */

 

算法2【贪婪算法】：Dijistra算法

算法思路：它和算法1中的原理有点像，但是引入了一个优先队列，每次进行移动都是从耗时最小的那个位置开始移动并且更新队列，当出现第一个到达目的地的数据 时，这个数据就是最快的数据

package com.cnblogs.mufasa.demo1;

import java.util.PriorityQueue;
import java.util.Scanner;

public class Answer1_2 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        String line = scanner.nextLine();
        int n = Integer.parseInt(line);
        int[][] area = new int[n][n];

        for (int i = 0; i < n; i++) {
            line = scanner.nextLine();
            String[] split = line.split(",");
            if (split.length != n) {
                throw new IllegalArgumentException("错误输入");
            }
            int j = 0;
            for (String num : split) {
                area[i][j++] = Integer.parseInt(num);
            }
        }

        int minimumTimeCost = getMinimumTimeCost(n,area);
        System.out.println(minimumTimeCost);
    }
    /** 请完成下面这个函数，实现题目要求的功能 **/
    /** 当然，你也可以不按照这个模板来作答，完全按照自己的想法来 ^-^  **/
    private static int getMinimumTimeCost(int n, int[][] area) {//贪婪算法，每次对优先队列的最小对象进行操作
        long startTime =  System.currentTimeMillis();
        PriorityQueue<Loc> queue=new PriorityQueue<>(3*n);//最小堆实现优先队列
        for(int i=0;i<n;i++){//初始化触发机关的位置
            queue.add(new Loc(1,i,area[1][i]));
        }
        Loc preLoc;
        while (true){
            preLoc=queue.poll();
            if(preLoc.index0==n-1){//已经到达目的地
                break;
            }
            if(preLoc.index1==n-2||preLoc.index1==n-1){//右边界情况，只能向下
                queue.add(new Loc(preLoc.index0+2,preLoc.index1,preLoc.times+area[preLoc.index0+2][preLoc.index1]));
            }else {//可以向下、向右
                queue.add(new Loc(preLoc.index0+2,preLoc.index1,preLoc.times+area[preLoc.index0+2][preLoc.index1]));
                queue.add(new Loc(preLoc.index0,preLoc.index1+2,preLoc.times+area[preLoc.index0][preLoc.index1+2]));
            }
        }
        long endTime =  System.currentTimeMillis();
        System.out.println(endTime-startTime);
        return preLoc.times;
    }
    static class Loc implements Comparable{
        public int times;
        public int index0,index1;
        public Loc(int index0,int index1,int times){
            this.index0=index0;
            this.index1=index1;
            this.times=times;
        }
        @Override
        public int compareTo(Object obj) {
            return times-((Loc)obj).times;
        }
    }
}

/*
8
35,92,98,68,35,65,26,72
29,78,83,16,5,89,92,28
48,51,37,79,65,74,50,71
98,78,99,57,1,30,22,16
72,88,55,33,56,58,28,49
4,28,29,20,18,61,11,73
61,19,47,34,85,32,77,89
29,49,10,81,52,5,63,25
 */

 

问题2描述：

①若干男女生围成一圈；

②求身边女生个数最多的男生位置，个数相同去最先出现的同学；

③求男生最大的团体人数，其中最多可以包含k个女士；

 

举一反三

问题描述：

现有一个长度为n的序列，需要你求出最长的非增子序列，使得其长度最长，并且这个子序列是满足非增性质的。输出最长长度

输入样例：

5

1 2 1 3 4

输出样例：

4

其中有如下满足要求的子序列：

① 1 2 3 4；②1 1 3 4