雷达无线电系列（一）几种常见的幅度分布函数（matlab）

文件下载地址：

https://github.com/mufasa007/myblog/tree/master/%E9%9B%B7%E8%BE%BE%E6%97%A0%E7%BA%BF%E7%94%B5%E7%B3%BB%E5%88%97%EF%BC%88%E4%B8%80%EF%BC%89%E5%87%A0%E7%A7%8D%E5%B8%B8%E8%A7%81%E7%9A%84%E5%B9%85%E5%BA%A6%E5%88%86%E5%B8%83%E5%87%BD%E6%95%B0%EF%BC%88matlab%EF%BC%89

 

一，瑞利幅度分布模型

　　① 常规模型

  

?

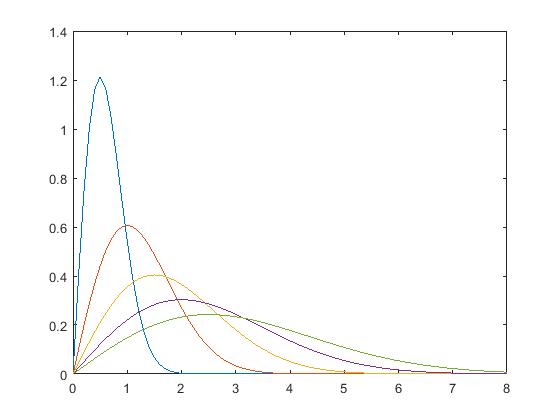
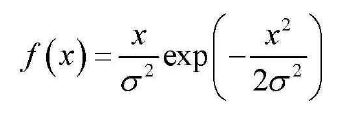
1 2 3 4 5 6

function [fx, Fx, Exn, Ex] = pdf_rayleigh(x, sigma, n) fx = x./(sigma.^2).*exp(-1.*x.^2./(2.*sigma.^2)); Fx = 1 - exp(-x.^2/(2.*sigma.^2)); Exn = 2.^(n./2).*sigma.^2.*gamma(1+n./2); Ex = sqrt(pi/(2.*sigma)); end

 　　

　　②AB模型

  

?

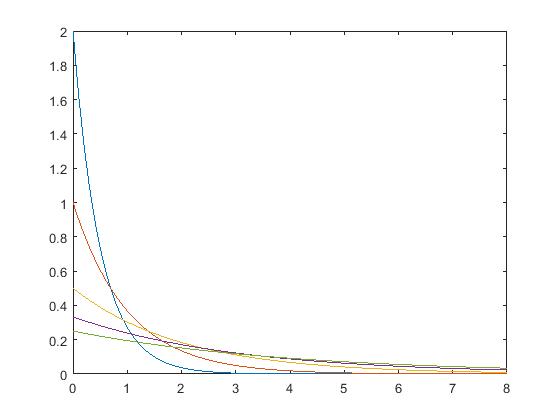
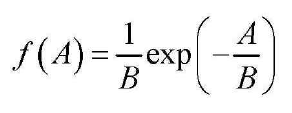
1 2 3

function [fA] = pdf_ABrayleigh(A, B) fA = 1/B.*exp(-1.*(A/B)); end

　　

二，对数正态分布模型

   

?

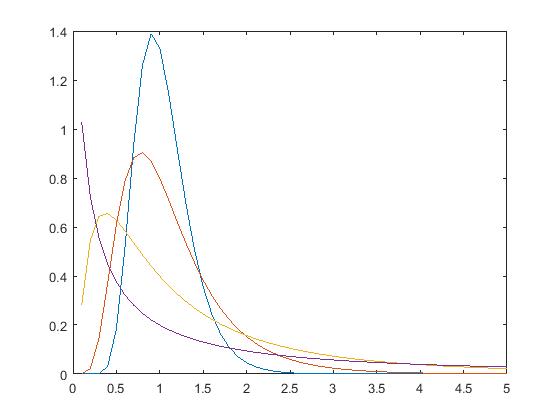
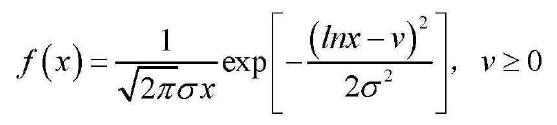
1 2 3 4 5 6 7

function [fx, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, v, n) fx = 1./(sqrt(2.*pi).*sigma.*x).*exp(-1.*(log(x)-v).^2./(2.*sigma.^2)); Fx = 1 - exp(-((log(x)-v)/sigma).^2/(2.*sigma.^2)); Exn = exp(1/2.*(n.*sigma).^2+n.*v); Ex = v.*exp((sigma.^2)/2); Dx = v.^2.*exp(sigma.^2).*(exp(sigma.^2)-1); end

 

三，韦布尔幅度分布模型

  

?

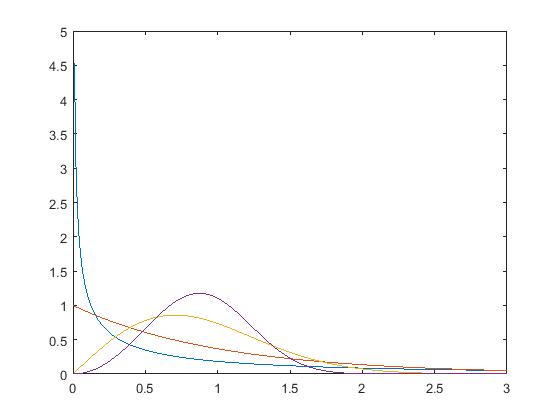
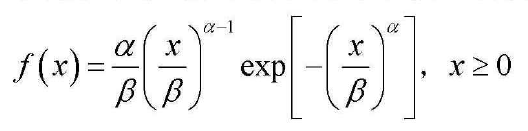
1 2 3 4 5 6 7

function [fx, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, beta, n) fx = alpha./beta.*(x./beta).^(alpha-1).*exp(-(x./beta).^alpha); Fx = 1 - exp(-(x./beta).^alpha); Exn = beta.^n.*gamma(n./alpha+1); Ex = beta.*gamma(1./alpha+1); Dx = beta.^2.*(gamma(2./alpha + 1) - gamma(1./alpha + 1).^2); end

　

四，k分布

  

?

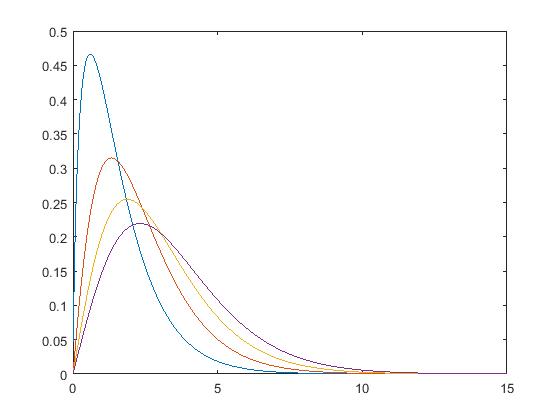
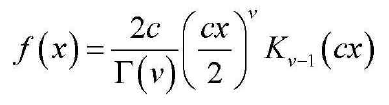
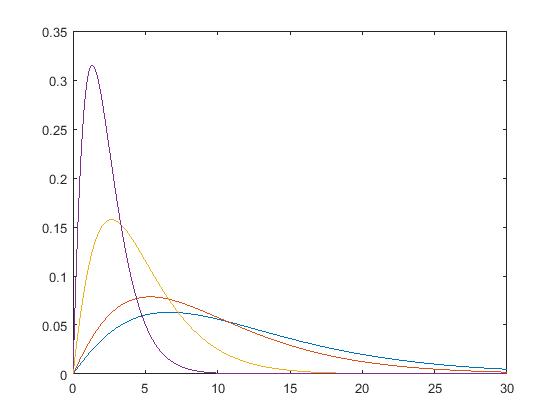
1 2 3 4 5

function [fx, Fx, Exn] = pdf_k(x, c, v, n) fx = (2.*c./gamma(v)).*(c.*x./2).^v.*besselk(v-1,c.*x); Fx = 1 - 2./gamma(v).*(c.*x./2).^v.*besselk(v,c.*x); Exn = gamma(n./2+1).*gamma(n./2+v)./gamma(v).*(2./c).^n; end

　　

五，Gamma分布

   

?

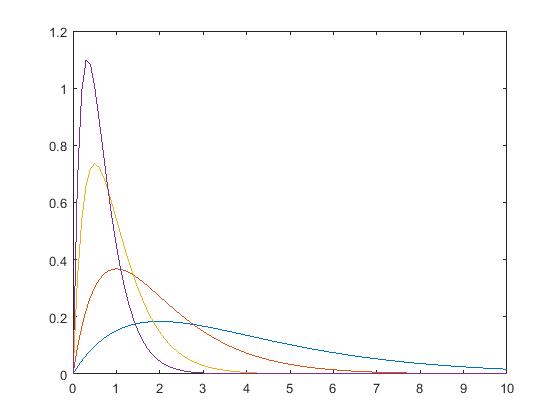
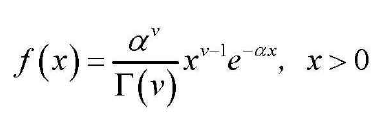
1 2 3 4 5

function [fx, Ex, Dx] = pdf_gamma(x, v, alpha) fx = alpha.^v/gamma(v).*x.^(v-1).*exp(-alpha.*x); Ex = v/alpha; Dx = v/alpha^2; end

　　

 六，测试运行程序

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114

clc; %% 测试k分布v参数 % x = 0:0.01:15; % c=1; % n=1; % figure; % [fx0, Fx, Exn] = pdf_k(x, c, 1, n); % [fx1, Fx, Exn] = pdf_k(x, c, 2, n); % [fx2, Fx, Exn] = pdf_k(x, c, 3, n); % [fx3, Fx, Exn] = pdf_k(x, c, 4, n); % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n); % plot(x,fx0, x,fx1, x,fx2, x,fx3);   %% 测试k分布c参数 % x = 0:0.01:30; % v=2; % n=1; % figure; % [fx0, Fx, Exn] = pdf_k(x, 0.2, v, n); % [fx1, Fx, Exn] = pdf_k(x, 0.25, v, n); % [fx2, Fx, Exn] = pdf_k(x, 0.5, v, n); % [fx3, Fx, Exn] = pdf_k(x, 1, v, n); % % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n); % plot(x,fx0, x,fx1, x,fx2, x,fx3);     %% 测试韦布尔分布beta参数 % x = 0:0.01:8; % alpha=3; % n=1; % figure; % [fx0, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, 1, n); % [fx1, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, 2, n); % [fx2, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, 3, n); % [fx3, Fx, Exn, Ex, Dx] = pdf_weibull(x, alpha, 4, n); % % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n); % plot(x,fx0, x,fx1, x,fx2, x,fx3);   %% 测试韦布尔分布alpha参数 % x = 0:0.01:3; % beta=1; % n=1; % figure; % [fx0, Fx, Exn, Ex, Dx] = pdf_weibull(x, 0.5, beta, n); % [fx1, Fx, Exn, Ex, Dx] = pdf_weibull(x, 1, beta, n); % [fx2, Fx, Exn, Ex, Dx] = pdf_weibull(x, 2, beta, n); % [fx3, Fx, Exn, Ex, Dx] = pdf_weibull(x, 3, beta, n); % % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n); % plot(x,fx0, x,fx1, x,fx2, x,fx3);     %% 测试对数正态v参数 % x = 0:0.1:20; % sigma=1; % n=1; % figure; % [fx0, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, 0.5, n); % [fx1, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, 1, n); % [fx2, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, 2, n); % [fx3, Fx, Exn, Ex, Dx] = pdf_lognormal(x, sigma, 3, n); % % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n); % plot(x,fx0, x,fx1, x,fx2, x,fx3);   %% 测试对数正态sigma参数 % x = 0:0.1:5; % v=0; % n=1; % figure; % [fx0, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 0.3, v, n); % [fx1, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 0.5, v, n); % [fx2, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 1, v, n); % [fx3, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2, v, n); % % [fx4, Fx, Exn, Ex, Dx] = pdf_lognormal(x, 2.5, v, n); % plot(x,fx0, x,fx1, x,fx2, x,fx3);   %% 测试rayleigh_AB分布函数 % figure; % x=0:0.1:8; % [fx0] = pdf_ABrayleigh(x, 0.5); % [fx1] = pdf_ABrayleigh(x, 1); % [fx2] = pdf_ABrayleigh(x, 2); % [fx3] = pdf_ABrayleigh(x, 3); % [fx4] = pdf_ABrayleigh(x, 4); % plot(x,fx0, x,fx1, x,fx2, x,fx3, x,fx4);   %% 测试rayleigh分布函数 % n = 1; % figure; % [fx0, Ex0, Dx0] = pdf_rayleigh(x, 0.5, n); % [fx1, Ex1, Dx1] = pdf_rayleigh(x, 1, n); % [fx2, Ex2, Dx2] = pdf_rayleigh(x, 1.5, n); % [fx3, Ex3, Dx3] = pdf_rayleigh(x, 2, n); % [fx4, Ex4, Dx4] = pdf_rayleigh(x, 2.5, n); % plot(x,fx0, x,fx1, x,fx2, x,fx3, x,fx4);   %% 测试gamma分布v参数 % x = 0:0.1:10; % alpha = 1; % figure; % [fx0, Ex0, Dx0] = pdf_gamma(x, 0.5, alpha); % [fx1, Ex1, Dx1] = pdf_gamma(x, 1, alpha); % [fx2, Ex2, Dx2] = pdf_gamma(x, 2, alpha); % [fx3, Ex3, Dx3] = pdf_gamma(x, 3, alpha); % plot(x,fx0, x,fx1, x,fx2, x,fx3);   %% 测试gamma分布alpha参数 % x = 0:0.1:10; % alpha = 1; % figure; % [fx0, Ex0, Dx0] = pdf_gamma(x, v, 0.5); % [fx1, Ex1, Dx1] = pdf_gamma(x, v, 1); % [fx2, Ex2, Dx2] = pdf_gamma(x, v, 2); % [fx3, Ex3, Dx3] = pdf_gamma(x, v, 3); % plot(x,fx0, x,fx1, x,fx2, x,fx3);