AcWing1027

AcWing1027.方格取数

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

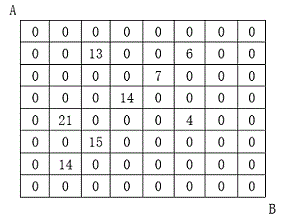
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式

第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 \(1\) 开始。

一行“0 0 0”表示结束。

输出格式

输出一个整数，表示两条路径上取得的最大的和。

数据范围

\(N \le 10\)

输入样例：

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例：

67

这个问题的关键就是如何处理同一个格子不能被重复选择

它要取两次数，每次取完后格子会清零，我们并不好利用搜索去实现。

我们可以当成两个人同时在图内取数，有向右向下两种前进方式，在相同时间内两人走的路径长度是一致的，最后两个人都走到右下角。

两次行走当成两个人，两个人以同样的速度，1s走1格前往右下角，第0s时两人位于（0，0），两人走的路径长度为k时，横坐标处于i1，i2的两人取得的数字之和的最大值。

dp[k][i1][i2]表示当两人离开(0, 0) k 步，两人横坐标分别为i1 i2，此时取得的数字之和最大值

不难发现，某一秒内，两人走的方向有四种情况

• i1向下，i2向下
• i1向下，i2向右
• i1向右，i2向下
• i1向右，i2向右

我们选出最大值即可

这道题的关键点，当i1和i2都走到同一个点，我们只能取一次，特判一下即可。

最后的答案是两人走了2n步都走到右下角时取出数的最大值dp[n + n][i1][i2]。

#include<bits/stdc++.h>
#define int long long

using namespace std;

const int N = 25;

int n;
int g[N][N], dp[N][N][N];

void solve()
{
    cin >> n;
    while (1)
    {
        int a, b, c;
        cin >> a >> b >> c;
        if (a == 0 && b == 0 && c == 0) break;
        g[a][b] = c;
    }
    for (int k = 2; k <= 2 * n; k ++ )
        for(int i1 = 1; i1 <= n; i1 ++ )
            for (int i2 = 1; i2 <= n; i2 ++ )
            {
                int j1 = k - i1, j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = g[i1][j1];
                    if (i1 != i2) t += g[i2][j2]; //如果当前i1 j1坐标不重合
                    dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][i1 - 1][i2 - 1] + t); //下 下
                    dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][i1 - 1][i2] + t); //下 右
                    dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][i1][i2 - 1] + t); //右 下
                    dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][i1][i2] + t); //右 右
                }
            }
    cout << dp[2 * n][n][n] << endl;
}

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    
    solve();

    return 0;
}