Codeforces Round 943 Div. 3 (A - D)
Codeforces Round 943 Div. 3
A
给你一个整数 \(x\) 。你的任务是找出任意一个整数 \(y\) \((1\le y \lt x)\) ，使得 \(\gcd(x,y)+y\) 为最大可能数。 \((1\le y \lt x)\) 使得 \(\gcd(x,y)+y\) 最大。
注意，如果有一个以上的 \(y\) 满足该语句，则允许你找出任何一个。
\(\gcd(a,b)\) 是 \(a\) 和 \(b\) 的最大公约数。例如， \(\gcd(6,4)=2\) 。
思路
暴力
代码实现
#include <bits/stdc++.h>
using namespace std;
#define int long long
int T;
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
void solve()
{
int x;
cin >> x;
int res = 0;
int pos = 0;
for (int i = 1; i < x; i ++ )
{
if (res < (gcd(x, i) + i))
{
res = gcd(x, i) + i;
pos = i;
//cout << gcd(x, i) << endl;
}
}
cout << pos << endl;
return;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> T;
while (T -- )
{
solve();
}
return 0;
}
B
给你两个二进制字符串 \(a\) 和 \(b\) 。二进制字符串是由字符 "0 "和 "1 "组成的字符串。
您的任务是确定最大可能的数字 $$k$$ ，使得长度为 $$k$$ 的字符串 $$a$$ 的前缀是字符串 $$b$$ 的子序列。
如果 \(a\) 可以从 \(b\) 中删除几个 (可能是零个或全部) 元素，那么序列 \(a\) 就是序列 \(b\) 的子序列。
思路
双指针
代码实现
#include <bits/stdc++.h>
using namespace std;
#define int long long
int T;
int n, m;
string a, b;
void solve()
{
cin >> n >> m;
cin >> a >> b;
int res = 0;
for (int i = 0, j = 0; i < n && j < m; i ++ )
{
if (a[i] == b[j])
{
res ++ ;
j ++ ;
}
else
{
while (a[i] != b[j] && j < m)
{
j ++ ;
}
if (j < m) res ++ ;
j ++ ;
}
}
cout << res << endl;
return;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> T;
while (T -- )
{
solve();
}
return 0;
}
C
Assembly via Remainders
每次测试时限：2 秒
每次测试的内存限制：256 兆字节
输入：标准输入
输出：标准输出
给你一个数组 $ x_2,x_3,\dots,x_n $ 。你的任务是找出任意一个数组$ a_1,\dots,a_n$ ，其中：
- 所有 $ 1\le i\le n $ 均为 $ 1\le a_i\le 10^9 $ 。
- $ x_i=a_i \bmod a_{i-1} $ 代表所有 $ 2\le i\le n $ 。
这里的 \(c\bmod d\) 表示整数 \(c\) 除以整数 \(d\) 的余数。例如， \(5 \bmod 2 = 1\) ， \(72 \bmod 3 = 0\) ， \(143 \bmod 14 = 3\) 。
注意，如果有一个以上的 \(a\) 满足该语句的要求，你可以找到任何一个。
输入格式
第一行包含一个整数 \(t\) 。 $ (1\le t\le 10^4) $ - 测试用例的数量。
每个测试用例的第一行包含一个整数 $ n $ $ (2\le n\le 500) $ -表示 \(a\) 数组中的元素个数 。
每个测试用例的第二行包含 \(n-1\) 个整数 $ x_2,\dots,x_n $ $ (1\le x_i\le 500) $ 。 $ (1\le x_i\le 500) $ - \(x\) 中的元素。
保证所有测试用例中 \(n\) 的值之和不超过 \(2 \cdot 10^5\) 。
输出格式
对于每个测试用例，输出满足语句要求的 $ a_1,\dots,a_n $ ( $ 1 \le a_i \le 10^9 $ )
样例输入 #1
5
4
2 4 1
3
1 1
6
4 2 5 1 2
2
500
3
1 5
样例输出 #1
3 5 4 9
2 5 11
5 14 16 5 11 24
501 500
2 7 5
提示
In the first test case $ a=[3,5,4,9] $ satisfies the conditions, because:
- $ a_2\bmod a_1=5\bmod 3=2=x_2 $ ;
- $ a_3\bmod a_2=4\bmod 5=4=x_3 $ ;
- $ a_4\bmod a_3=9\bmod 4=1=x_4 $ ;
思路
本题要我们构造\(a_i\) 使得$ a_i \bmod a_{i-1} = x_i$，
有一个非常巧妙的思路
当\(a_i < a_{i - 1}\)时， \(a_i \bmod a_{i-1}\) 的值就是\(a_i\)
同理可推，当\(a_i = a_{i - 1} + x\)， \(a_i \bmod a_{i-1}\) 的值就是\(x\)
但有个前提条件 \(\lfloor \frac {x}{a_{i - 1}} \rfloor = 0\) ，这样才能保证\(a_i \bmod a_{i-1} = x\) 非常关键！
也就是说我们需要保证 \(a_i\)相比\(a_{i - 1}\)多的\(x\) 不能被\(a_{i - 1}\)给取模掉一部分，也就是要保证\(x \bmod a_{i - 1} = x\)，也就是需要保证所有的\(x < a_{i - 1}\)
举个例子
当\(x = 5, a_{i - 1} = 3\)，根据我们得出的结论 \(a_i = 8\)，但实际上\(8 \bmod 3 = 2\)，因为 \(\lfloor \frac {x}{a_{i - 1}} \rfloor = 1\)，这就导致推出的\(a_i\)不正确
题目限制了$ (1\le x_i\le 500) \(，保证所有的\)x < a_{i - 1}\(，也就是说\)a_{i - 1} > 500\(，才能保证在所有\)x\(取值的情况下，均不会出现自身被\)a_{i - 1}\(给取模掉一部分，保证\)x \bmod a_{i - 1} = x$
代码实现
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 510;
int T;
int n;
int b[N], a[N];
void solve()
{
cin >> n;
for (int i = 2; i <= n; i ++ ) cin >> b[i]; //这里存的数组范围注意下
a[1] = 600; //关键点！ a[1]选一个大于500的数赋值
for (int i = 2; i <= n; i ++ )
{
a[i] = a[i - 1] + b[i];
}
for (int i = 1; i <= n; i ++ ) cout << a[i] << " ";
cout << endl;
return;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> T;
while(T -- )
{
solve();
}
return 0;
}
D
Permutation Game
Bodya 和 Sasha 发现了一个排列 \(p_1,\dots,p_n\) 和一个数组 \(a_1,\dots,a_n\)。他们决定玩一个著名的 "排列游戏"。
长度为 \(n\) 的排列是由 \(n\) 个不同的整数组成的数组，这些整数从\(1\) 到 \(n\) 按任意顺序排列。例如， \([2,3,1,5,4]\) 是一个排列，但 \([1,2,2]\) 不是一个排列( \(2\) 在数组中出现了两次)， \([1,3,4]\) 也不是一个排列 ( \(n=3\) ，但数组中有 \(4\) )。
它们都在排列中选择了一个起始位置。
对局持续了\(k\) 个回合。棋手同时下棋。在每个回合中，每个棋手都会发生两件事：
- 如果棋手当前的位置是 \(x\) ，他的得分就会增加 \(a_x\) 。
- 然后棋手要么停留在当前位置 \(x\) ，要么从 \(x\) 移动到 \(p_x\)。
在整整 \(k\) 个回合后，得分较高的一方即为游戏的获胜者。
已知博迪亚的起始位置 \(P_B\) 和萨沙的起始位置 \(P_S\) ，如果两位棋手都想获胜，请判断谁会赢得对局。
输入
第一行包含一个整数 \(t\) ( \(1\le t\le 10^4\) )。( \(1\le t\le 10^4\) )--测试用例数。
每个测试用例的第一行分别包含整数 \(n\), \(k\), \(P_B\), \(P_S\) (\(1\le P_B,P_S\le n\le 2\cdot 10^5\), \(1\le k\le 10^9\)) --排列长度、游戏持续时间、起始位置。
下一行包含 \(n\) 个整数 \(p_1,\dots,p_n\) ( \(1 \le p_i \le n\) ) - 排列 \(p\) 的元素。
下一行包含 \(n\) 个整数 \(a_1,\dots,a_n\) ( \(1\le a_i\le 10^9\) ) - 数组 \(a\) 的元素。
保证所有测试用例中 \(n\) 的值之和不超过 \(2 \cdot 10^5\) 。
Output
For each testcase output:
- "Bodya" if Bodya wins the game.
- "Sasha" if Sasha wins the game.
- "Draw" if the players have the same score.
样例输入 #1
10
4 2 3 2
4 1 2 3
7 2 5 6
10 8 2 10
3 1 4 5 2 7 8 10 6 9
5 10 5 1 3 7 10 15 4 3
2 1000000000 1 2
1 2
4 4
8 10 4 1
5 1 4 3 2 8 6 7
1 1 2 1 2 100 101 102
5 1 2 5
1 2 4 5 3
4 6 9 4 2
4 2 3 1
4 1 3 2
6 8 5 3
6 9 5 4
6 1 3 5 2 4
6 9 8 9 5 10
4 8 4 2
2 3 4 1
5 2 8 7
4 2 3 1
4 1 3 2
6 8 5 3
2 1000000000 1 2
1 2
1000000000 2
样例输出 #1
Bodya
Sasha
Draw
Draw
Bodya
Sasha
Sasha
Sasha
Sasha
Bodya
Note
Below you can find the explanation for the first testcase, where the game consists of \(k=2\) turns.
| Turn | Bodya's position | Bodya's score | Bodya's move | Sasha's position | Sasha's score | Sasha's move |
|---|---|---|---|---|---|---|
| first | \(3\) | \(0 + a_3 = 0 + 5 = 5\) | stays on the same position | \(2\) | \(0 + a_2 = 0 + 2 = 2\) | moves to \(p_2=1\) |
| second | \(3\) | \(5 + a_3 = 5 + 5 = 10\) | stays on the same position | \(1\) | \(2 + a_1 = 2 + 7 = 9\) | stays on the same position |
| final results | \(3\) | \(10\) | \(1\) | \(9\) |
As we may see, Bodya's score is greater, so he wins the game. It can be shown that Bodya always can win this game.
思路
题意：在k个回合内博迪亚和萨沙可以在坐标为1-n的不同位置间移动，每一个点都对应一个分数，一个回合内可以选择继续留在当前位置x 或者 移动到p[x]点 以追求更大的得分，k个回合后，看谁的总得分最多
点x只能移动到点p[x]
某一点x的得分是a[x]
使得程序不会TLE的关键点：我们可以发现走n次不停留一定能回到起始点，在这个过程中我们就一定可以找到得分最大的点，然后在这个得分最大的点一直呆下去就是总得分最大的情况，所以我们最多只用枚举n次，找到得分最大的点即可，剩下的\(k - n\)个回合我们就呆在这个得分最大的点就可以了，所以当\(k > n\)时，我们最多只用遍历n次，就能到达得分最大的点
如果我们对于每一回合都遍历，也就是k次，k的最大取值达到\(10^9\)，就会TLE
利用博迪亚的得分路线来举例
我们用nowb表示博迪亚走到当前位置x所得总分，也就是前i个回合的总得分，sb的值是 在x的上一个点停留至回合结束总得分 和 在点x停留至回合结束的总得分的最大值 ，也就是说当我们遍历完能走到的点，对于每个点前i个回合走到该点并让其在剩下的k - i个回合停留在这个点的总得分，遍历完能走到的点，取出总得分的最大值
-
当 \(k < n\)，我们最多走\(k\)个点
-
当 \(k >= n\)，我们就能把n个点全走完，找出在这n个点停留后产生的总得分最大值
看代码内更清楚
代码实现
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10;
int T;
int n, k , pb, ps;
int p[N], a[N];
void solve()
{
cin >> n >> k >> pb >> ps;
for (int i = 1; i <= n; i ++ ) cin >> p[i];
for (int i = 1; i <= n; i ++ ) cin >> a[i];
//一定得写在solve()内, 避免上一个测试用例内的数据污染
int sb = 0, ss = 0; //分别记录博迪亚和萨沙从初始位置移动到当前位置后固定在当前位置直到回合结束的最大得分
int npb = 0, nps = 0; //记录博迪亚和萨沙的当前位置
int nowb = 0, nows = 0; //记录博迪亚和萨沙前i次回合的总得分
npb = pb, nps = ps; //从题目里给的初始位置开始移动
for (int i = 1; i <= n && i <= k; i ++ )//当k<n时, 移动k次 当k>n时，移动n次就不用移动了 不加i <= n就会TLE
{
nowb += a[npb], nows += a[nps]; //加上当前回合移动到本位置产生的得分
sb = max(sb, nowb + (k - i) * a[npb]); //取出博迪亚 移动到当前位置并固定在当前位置产生的总得分 和 固定在上一个位置的总得分 的最大值
ss = max(ss, nows + (k - i) * a[nps]); //取出萨沙最大值
npb = p[npb], nps = p[nps]; //移动到下一位置
}
if (sb > ss) cout << "Bodya" << endl;
else if (sb < ss) cout << "Sasha" << endl;
else cout << "Draw" << endl;
return;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> T;
while (T -- )
{
solve();
}
return 0;
}
刚开始想用dfs的思路做，但会TLE＋MLE
k最多只能开到20
我认为原因是这样的
每一层dfs函数内都有t = max(dfs(x, u + 2, t + a[x]), dfs(p[x], u + 2, t + a[p[x]]));，分成两支向下搜索，就像一个二叉树一样，复杂度大约为\(2^n\)，c++合理操作次数是\(10^7\)大约为\(2^{24}\)，导致复杂度极高，所以会TLE
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5 + 10;
int T;
int n, k , pb, ps;
int p[N], a[N];
int res, pos;
int dfs(int x, int u, int t)
{
if (u == k)
{
return t;
}
t = a[x];
t = max(dfs(x, u + 2, t + a[x]), dfs(p[x], u + 2, t + a[p[x]]));
return t;
}
void solve()
{
cin >> n >> k >> pb >> ps;
for (int i = 1; i <= n; i ++ ) cin >> p[i];
for (int i = 1; i <= n; i ++ ) cin >> a[i];
res = dfs(pb, 0, 0);
pos = dfs(ps, 0, 0);
//cout << pos << endl;
if (res > pos) cout << "Bodya" << endl;
else if (res < pos) cout << "Sasha" << endl;
else cout << "Draw" << endl;
return;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> T;
//while (T -- )
{
solve();
}
return 0;
}
E
Cells Arrangement
time limit per test: 2 seconds
memory limit per test: 256 megabytes
input: standard input
output: standard output
给你一个整数 \(n\) 。您在网格 \(n\times n\) 中选择 \(n\) 单元格 \((x_1,y_1), (x_2,y_2),\dots,(x_n,y_n)\) ，其中 \(1\le x_i\le n\) 和 \(1\le y_i\le n\) 。
让 \(\mathcal{H}\) 成为任意一对单元格之间不同的曼哈顿距离集合。你的任务是最大化 \(\mathcal{H}\) 的大小。注释中给出了集合及其构造的例子。
如果存在多个解，你可以输出任意一个。
单元格 \((x_1,y_1)\) 和 \((x_2,y_2)\) 之间的曼哈顿距离等于 \(|x_1-x_2|+|y_1-y_2|\) 。
输入
第一行包含一个整数 \(t\) ( \(1\le t\le 50\) ) - 测试用例数。
下面每行 \(t\) 都包含一个整数 \(n\) ( \(2\le n\le 10^3\) )。
输出
对于每个测试用例，输出 \(n\) 个点，使 \(\mathcal{H}\) 的大小达到最大。无需在每个测试用例的答案末尾输出空行。
样例 #1
样例输入 #1
5
2
3
4
5
6
样例输出 #1
1 1
1 2
2 1
2 3
3 1
1 1
1 3
4 3
4 4
1 1
1 3
1 4
2 1
5 5
1 4
1 5
1 6
5 2
5 5
6 1
提示
In the first testcase we have $ n=2 $ . One of the possible arrangements is:
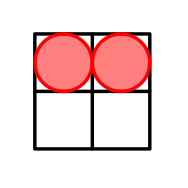The arrangement with cells located in $ (1,1) $ and $ (1,2) $ . In this case $ \mathcal{H}={|1-1|+|1-1|,|1-1|+|2-2|,|1-1|+|1-2|}={0,0,1}={0,1} $ . Hence, the size of $ \mathcal{H} $ is $ 2 $ . It can be shown that it is the greatest possible answer.In the second testcase we have $ n=3 $ . The optimal arrangement is:
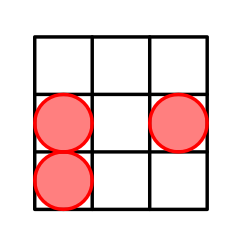The arrangement with cells located in $ (2,1) $ , $ (2,3) $ and $ (3,1) $ . $ \mathcal{H} $ = $ {|2-2|+|1-1|,|2-2|+|3-3|,|3-3|+|1-1|,|2-2|+|1-3|,|2-3|+|1-1|,|2-3|+|3-1|} $ = $ {0,0,0,2,1,3} $ = $ {0,1,2,3} $ .
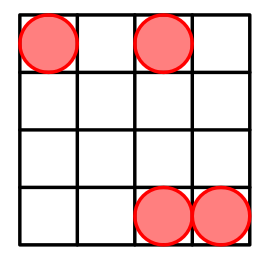
For $ n=4 $ a possible arrangement is:
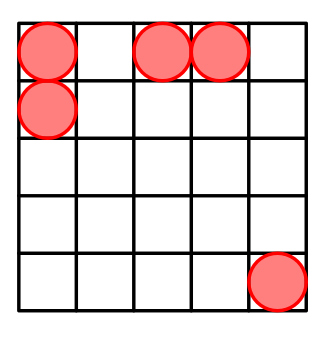
For $ n=5 $ a possible arrangement is:
For $ n=6 $ a possible arrangement is:
浙公网安备 33010602011771号