软件工程实践2017第二次作业
github传送门
阅读构建之法
由于书本买到得比较迟,看的内容不太多,其中印象比较深刻的是第二章中提到的单元测试和效能分析。作为一个好代码,是要经过大量效能分析后的改进,提炼而成的,不能盲目地去改代码,要通过性能分析工具测试后,得出代码的各部分函数耗时数据,找出相对耗时较长的部分,进行优化算法等,才是正确的代码改进方法。单元测试部分,我目前在自己的IDE中还无法实现...因此还不能说这部分功能有什么用途,暂且记此作笔记,以后再好好琢磨
单元测试好坏的标准如下:
1.单元测试应该在最低功能/参数上验证程序的正确性。
2.单元测试必须由最熟悉代码的人(程序的作者)来写
3.单元测试后,机器状态保持不变
4.单元测试要快(一个测试的运行时间是几秒钟,而不是几分钟)
5.单元测试应该产生可重复、一致的结果
6.独立性——单元测试的运行/通过/失败不依赖于别的测试,可以人为构造数据,以保持单元测试的独立性
7.单元测试应该覆盖所有代码路径(注意点:100%的代码覆盖率并不等同于100%的正确性!)
8.单元测试应该集成到自动测试的框架中
9.单元测试必须和产品代码一起保存和维护
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 20 | 30 |
| Development | 开发 | 720 | 855 |
| · Analysis | · 需求分析 (包括学习新技术) | 120 | 200 |
| · Design Spec | · 生成设计文档 | 40 | 20 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 50 | 0 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 20 | 20 |
| · Design | · 具体设计 | 30 | 35 |
| · Coding | · 具体编码 | 240 | 360 |
| · Code Review | · 代码复审 | 100 | 100 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 120 |
| Reporting | 报告 | 180 | 190 |
| · Test Report | · 测试报告 | 50 | 40 |
| · Size Measurement | · 计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 100 | 120 |
| · All | · 合计 | 920 | 1075 |
解决思路
- 归纳问题点
- git基本使用
- IDE的安装和使用
- 算法实现
- 性能分析
由于之前安装过VS2015,使用过git,这两个步骤可以跳过,然而VS2015的具体使用方法还不是很熟悉,在网上找了一篇比较适合新手的使用笔记。数独问题,小时候有一段时间感兴趣过,知道可以通过写出9行1~9的数字,然后通过一定的行列变换来生成。于是我的算法1.0就诞生了,通过随机次数的行列变换来生成数独,行列变换的原则是:交换只发生在前三行,中间三行,最后三行,前三列,中间三列以及最后三列之间,不能越界交换。兴高采烈地完成了第一次尝试之后,我测试了几个数据。然而运行结果出现了两个问题:1、数独终盘重复率高,并且生成效率十分低...这一点是我还没用性能分析工具就得出来的结论。。因为跑了半天才跳出来几十个数独终盘,用肉眼都感觉的出来这方法明显不适合题目要求的大量数据...于是我也不打算push到github上了,直接删了代码重新写(肉痛),看来只能用算法来解决此问题了。算法一直是我不擅长的部分,我思考了一阵,自己学过的遍历方法只有可怜的BFS和DFS.....再结合题目,要生成一个数独终盘,应该要用一些数字去尝试填进去,填到不符合的就要回到一个特定点,重新尝试填数字,结合算法特点,认为DFS比较可能实现。然而,不符合的条件是什么?返回到哪个结点?怎么返回?我上网搜了相关资料,发现大部分的文章都提到了回溯法,大致思想跟我之前思考的方法是一样的,但是展现了具体的回溯方法,回溯到的结点确认。即一个点一个点逐级向上回溯,例8行8列无法填入任何满足的数字,就回溯到8行7列,重填,再无法满足则返回8行6列,以此类推。而判断方法就简单了,避免行冲突,列冲突,格冲突。目前放在github代码的就是算法2.0 。
参考文章(http://blog.csdn.net/xiahn1a/article/details/50852849)
设计实现
由于作业的要求不是很复杂,我分了两个类
- class Judge
- function formatJudge
- class todoSudoku
- function numJudge
- function fill
- function shuf
- function shuf_first
- function outPut
- function toPrint
画了一个很奇怪的流程图...实在不太会画,抱歉
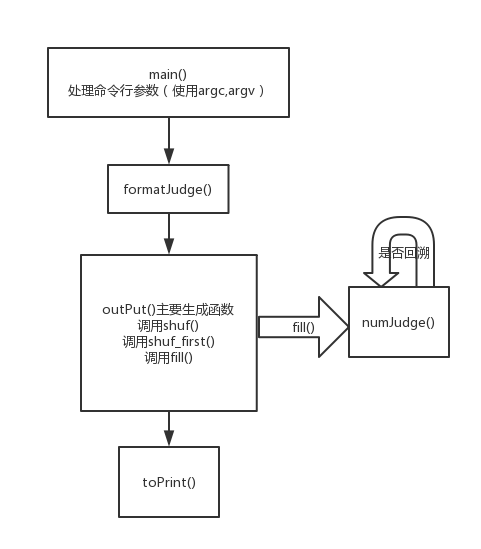
再补个代码大致思路。首先通过formatJudge()判断命令行输入参数格式是否正确,进入outPut(),outPut()中,若formatJudge()返回值为false则报错,若返回true则继续进行,通过shuf生成随机测试数组,通过shuf_first()生成包含题目要求的数独首列,即首行首列为固定数值,进入fill(),fill()采用回溯法,通过numJudge()来判断填入测试数组是否正确,最后生成数独终盘。
代码说明
- 判断参数格式
bool formatJudge() { //判断命令行输入的参数格式是否正确
if (para != "-c")
return false;
for (int k = 0; k < num_str.length(); k++) {
if (num_str[k] >= '9' || num_str[k] <= '0')
return false;
}
return true;
}
- 生成并输出数独终盘
void outPut(bool isRight) { //生成并输出数独终盘
if (isRight) { //若输入格式正确 则输出数独终盘
int cnt = atoi(num_str.c_str());
for (int k = 0; k < cnt; k++) {
shuf(temp);
shuf_first(arr[0]);
fill(1, 0, temp);
toPrint();
memset(temp, 0, sizeof(temp));
memset(arr, 0, sizeof(arr));
outfile << endl;
}
}
else { //若输入格式错误 则报错
cout << "Format Wrong!" << endl;
}
}
- 填入数独函数
bool fill(int y, int x, int* p) { //回溯法填入数字
if (y > 8)
return true;
if (numJudge(y, x, *p)) {
arr[y][x] = *p;
if (fill(y + (x + 1) / 9, (x + 1) % 9, temp))
return true;
}
arr[y][x] = 0;
if (p - temp >= 8)
return false;
if (fill(y, x, p + 1))
return true;
}
- 判断函数
bool numJudge(int i, int j, int num) { //判断填入数字是否符合数独原则
for (int k = 0; k < i; k++) //列判断
if (arr[k][j] == num)
return false;
for (int k = 0; k < j; k++) //行判断
if (arr[i][k] == num)
return false;
int count = i % 3 * 3 + j % 3;
while (count--) //块判断
if (!(arr[i - i % 3 + count / 3][j - j % 3 + count % 3] - num))
return false;
return true;
}
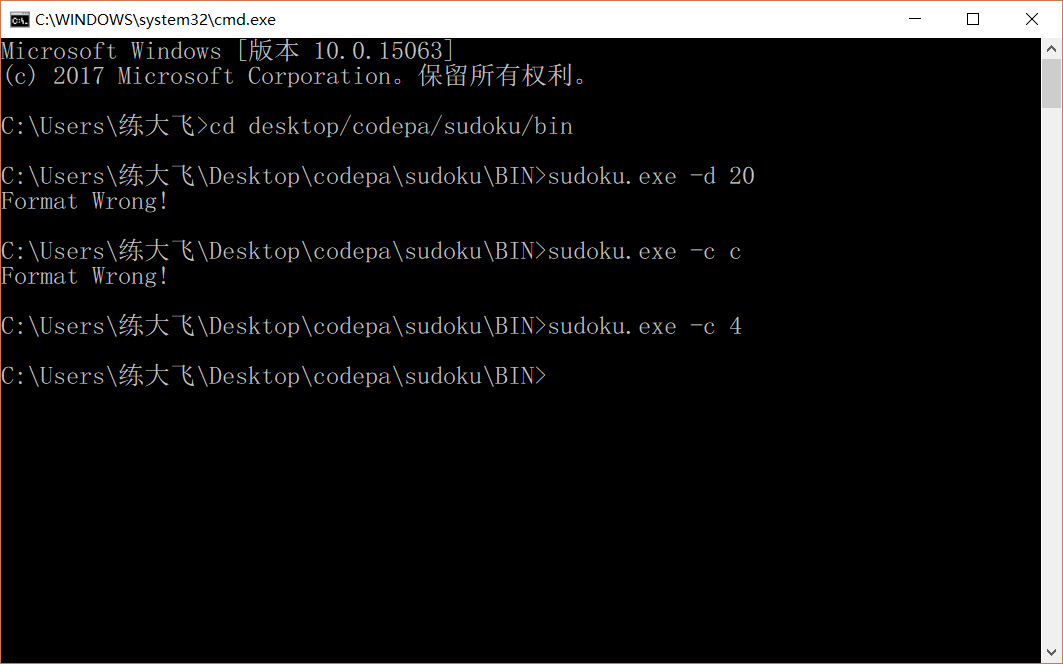
测试运行
性能分析图(1W的数据)
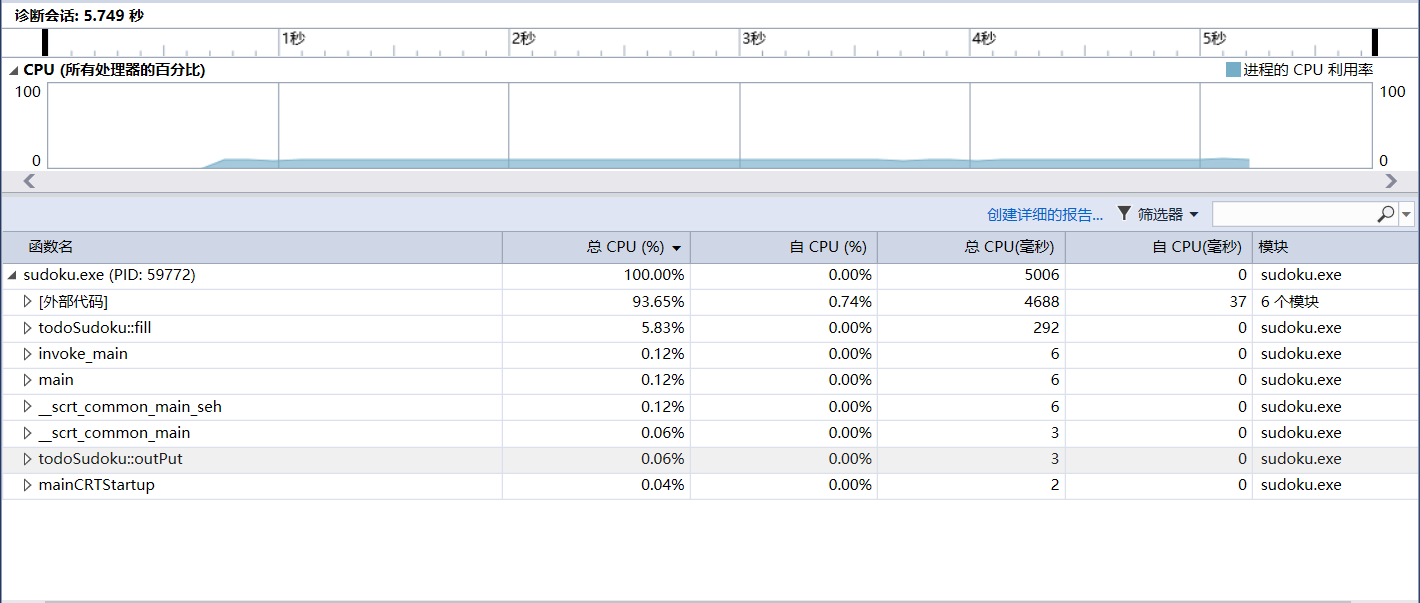

有图得知,我的一大部分时间竟然是在toPrint,输出数独函数上,目前想的方法就是用printf来替换cout会快一些。上网搜索了资料,发现,最快的竟然是putchar()函数,原因是输出字符是最高效的。第二耗时的部分就是fill(),也就是填充数字的部分。由于我算法能力比较差...本身就是参考网上的方法,只能推测,在numJudge()中,可以省略一些步骤。在块判断中,我的原方法是,从当前块中开始,逆顺序一个一个块往上判断,这样就会导致重复冗余。例如在第一次时从第8块开始往回判断,第7块和第6块都是正确的,用标记标注,那么第二次从第9块开始往回判断时,第7和第6块就不用重复判断了。这是目前的思路,但是代码实现还没完成。希望在接下来的努力中可以实现。



