[FJOI2007]轮状病毒

题目：洛谷P2144、BZOJ1002、codevs2886。

题目大意：给你n+1($n\le 100$)个节点，除第一个节点外的所有节点围绕第一个节点排列成环装。中间的节点和所有节点都能连边，环上相邻两个节点也能连边。问该图生成树的数量（即有多少种不同方法能用n条边连接所有节点）。

以下是n=3时的16种方案。

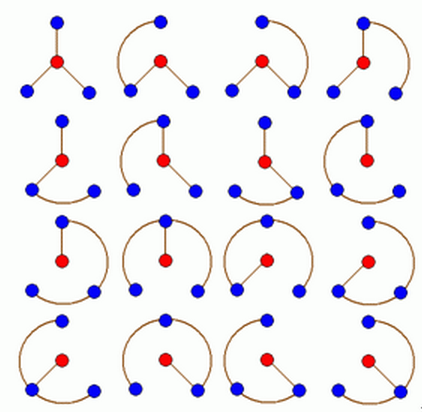
解题思路：此题n小于等于100，但是无法迅速找到能求出解的方法。

此类题目通常都有规律。

我们发现，当n=1、2、3、4、5时，答案分别为1、5、16、45、121，即$1^2$,$3^2-4$,$4^2$,$7^2-4$,$11^2$。

不考虑减4的情况，观察底数，是不是斐波那契数列的形态？

那么我们递推出该斐波那契数列，然后求出第n项的平方。

然后发现，n为偶数时需要减去4，那么减去4即可。

这就是此题的规律。

结果非常大，要用高精度。

C++ Code：

#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long
struct bg{
	ll a[700];
	int len;
}f[101];
void add(ll a[],int lena,ll b[],int lenb,ll c[],int& lenc){
	lenc=lena;
	if(lenc<lenb)lenc=lenb;
	for(int i=1;i<=lenc;++i){
		c[i]+=a[i]+b[i];
		c[i+1]+=c[i]/100000000;
		c[i]%=100000000;
	}
	while(c[lenc+1])++lenc;
}
void sqr$print(ll a[],int lena,int odd){
	ll b[700]={0};
	int lenb=(lena<<1)-1;
	for(int i=1;i<=lena;++i)
	for(int j=1;j<=lena;++j){
		b[i+j-1]+=a[i]*a[j];
		b[i+j]+=b[i+j-1]/100000000;
		b[i+j-1]%=100000000;
	}
	while(b[lenb+1])++lenb;
	while(!b[lenb])--lenb;
	if(!odd){
		int now=1;
		b[1]-=4;
		while(b[now]<0){
			b[now]+=100000000;
			--b[now++];
		}
	}
	while(b[lenb+1])++lenb;
	while(!b[lenb])--lenb;
	printf("%d",(int)b[lenb]);
	for(int i=lenb-1;i;--i)printf("%08d",(int)b[i]);
	putchar('\n');
}
int main(){
	memset(f,0,sizeof f);
	int n;
	scanf("%d",&n);
	f[1].a[1]=f[1].len=f[2].len=1;
	f[2].a[1]=3;
	for(int i=3;i<=n;++i)
	add(f[i-2].a,f[i-2].len,f[i-1].a,f[i-1].len,f[i].a,f[i].len);
	sqr$print(f[n].a,f[n].len,n&1);
	return 0;
}