[NOIP2016提高组]愤怒的小鸟

题目：UOJ#265、洛谷P2831、Vijos P2008。

题目大意：有n头猪，都在一个二维坐标系里（每头猪坐标为两位小数）。规定每只鸟能从（0,0）处发射，且经过的抛物线一定为$y=ax^2+bx$，且$a<0$。

如果几头猪头猪在同一条抛物线上，那么它就能被一只鸟打死。问至少发射多少只鸟才能打死所有的猪？

解题思路：由于n最大才18，我们可以用二进制的每一个位来保存一只鸟，做一个状压DP。

那么就是判断抛物线的事了。我们枚举两头猪，算出a和b的值。由于鸟从原点飞出，我们直接套公式计算即可。

计算形如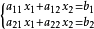的二元一次方程，直接套公式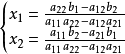即可。

然后判断a是否小于0即可。如果是，则说明存在这条抛物线，那我们继续枚举所有猪i，看是否在这条抛物线上，如果是就把1<<(i-1)的值加到抛物线上。

注意如果两头猪一样，那么该抛物线就是这一头猪。

最后类似背包的DP即可。

可以发现抛物线数量最坏是$n^2$级别的，所以时间复杂度$O(n^3+2^n n^2)$。

C++ Code：

#include<cstdio>
#include<cstring>
#include<cmath>
#define eps (1e-13)
using namespace std;
struct Vec{
	long double x,y;
}e[22];
int f[1<<22],g[666];
int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		int n,m;
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;++i)
		scanf("%Lf%Lf",&e[i].x,&e[i].y);
		int cnt=0;
		for(int i=1;i<=n;++i)
		for(int j=1;j<=n;++j)
		if(i!=j){
			long double a=(e[j].x*e[i].y-e[i].x*e[j].y)/(e[i].x*e[i].x*e[j].x-e[j].x*e[j].x*e[i].x),
				   b=(e[i].x*e[i].x*e[j].y-e[j].x*e[j].x*e[i].y)/(e[i].x*e[i].x*e[j].x-e[i].x*e[j].x*e[j].x);
			if(-a>eps){
				int num=0;
				for(int k=1;k<=n;++k)
				if(fabs(a*e[k].x*e[k].x+b*e[k].x-e[k].y)<eps)
				num|=1<<(k-1);
				g[++cnt]=num;
			}	
		}else
		g[++cnt]=1<<(i-1);
		memset(f,0x3f,sizeof f);
		f[0]=0;
		for(int i=0;i<(1<<n);++i)
		for(int j=1;j<=cnt;++j)
		if(f[i|g[j]]>f[i]+1)f[i|g[j]]=f[i]+1;
		printf("%d\n",f[(1<<n)-1]);
	}
	return 0;
}