787. Cheapest Flights Within K Stops

仅供自己学习

 

思路：

深搜和广搜都是能做的，但是需要进行剪枝。剪枝条件，如果该点访问过了就不对这个点继续DFS，如果K<0了且没到达目的点就返回不继续DFS，  如果当前的花费+新节点的花费大于之前的花费也返回不继续DFS。

DFS：

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
        unordered_map<int,vector<vector<int>>> edge;
        unordered_set<int> visited{{src}};
        int res=INT_MAX;
        for(const auto& ex:flights){
            edge[ex[0]].push_back({ex[1],ex[2]});
        }
        DFS(edge,src,dst,K,res,0,visited);
        return (res==INT_MAX)? -1:res;
    }

    void DFS(unordered_map<int,vector<vector<int>>>& edge,int cur,int dst,int K,int& res,int out,unordered_set<int>& visited){
        if(cur==dst){
            res=out;
            return;
        }
        if(K<0) return;
        for(const auto& flight:edge[cur]){
            if(visited.count(flight[0])||out+flight[1]>res) continue;
            visited.insert(flight[0]);
            DFS(edge,flight[0],dst,K-1,res,out+flight[1],visited);
            visited.erase(flight[0]);
        }
    }
};

 

这里有个问题，因为DFS不是return res，所以要传 res 的reference进入函数，这样才能改变参数。

 

DFS代码：

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
        unordered_map<int,vector<vector<int>>> edge;
        queue<vector<int>> q{{{src,0}}};  //第一个是当前节点，第二个是达到当前节点的花费总和
        int res=INT_MAX,cnt=0;
        for(const auto& ex:flights){
            edge[ex[0]].push_back({ex[1],ex[2]});
        }
        while(!q.empty()){
            for(int i=q.size();i>0;--i){
                auto t=q.front();
                q.pop();
                if(t[0]==dst) res=min(res,t[1]);
                for(const auto& a:edge[t[0]]){
                    if(t[1]+a[1]>res) continue;
                    q.push({a[0],t[1]+a[1]});
                }
            }
            if(cnt++>K) break;
        }
        return (res==INT_MAX)? -1:res;
    }
};

 

Bellman-ford：

根据伪代码及递归式

 

递归式为：

 

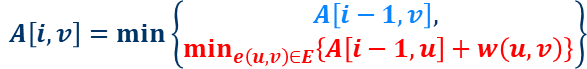
 伪代码：

 

可得到代码：

这是用了二维数组的，空间复杂度为O（n^2）

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
       vector<vector<int>> dp(K+2,vector<int>(n,1e9));
       dp[0][src] = 0;
       for(int i=1;i<=K+1;++i){
           dp[i][src]=0;
           for(auto& x:flights){
               dp[i][x[1]] = min(dp[i][x[1]],dp[i-1][x[0]]+x[2]);
           }　　//该递归式，如果有其他跳数跳到该点的距离更小就更新，i为跳数
       }
       return (dp[K+1][dst]>=1e9) ? -1:dp[K+1][dst];
    }
};

 

 下面是一维数组的

伪代码为：

 

 代码：

class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
       vector<int> dp(n,1e9);
       dp[src] = 0;
       for(int i=0;i<=K;++i){
           vector<int> temp=dp;
           for(auto& x:flights){
               temp[x[1]] = min(temp[x[1]],dp[x[0]]+x[2]);
           }
           dp = temp;
       }
       return (dp[dst]>=1e9) ? -1:dp[dst];
    }
};