牛客网暑期ACM多校训练营(第一场)
---恢复内容开始---
题意:计算多少种矩阵满足
Ai, j ∈ {0, 1, 2} for all 1 ≤ i ≤ n, 1 ≤ j ≤ m.
Ai, j ≤ Ai + 1, j for all 1 ≤ i < n, 1 ≤ j ≤ m.
Ai, j ≤ Ai, j + 1 for all 1 ≤ i ≤ n, 1 ≤ j < m.
这三条性质。
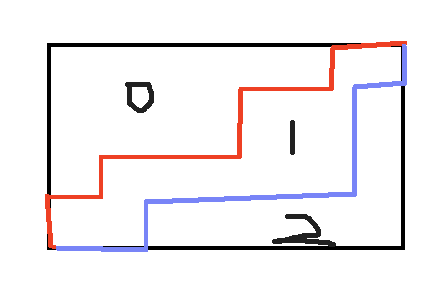
本题可以转换为询问有多少种存在两条路径从左下到右上,互相不穿过的矩阵

可以将矩阵向左上角平移一个单位,改询问为从A到B,从C到D有多少种合法路径
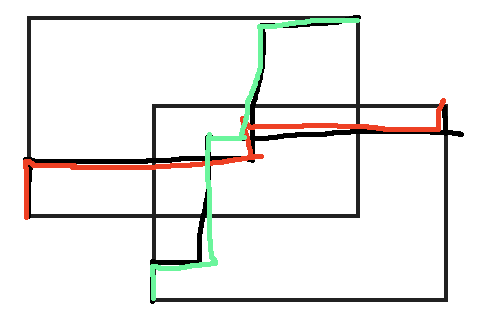
因此答案就是C(m+n,n)*C(m+n,n)-C(m+n,n-1)*C(m+n,m-1)
就是A到B的路径方案数*C到D的路径方案数减去不合法的路径方案数,不合法的就是相互穿过的路径,
相互穿过的路径,就是改道的路径

#include <iostream> #include <cstdio> #include <cmath> #include <algorithm> #include <map> #include <queue> #include <vector> #include <cstring> #include <iomanip> //#include <unordered_map> #include <set> #include <ctime> #include <sstream> #include <stack> //CLOCKS_PER_SEC #define se second #define fi first #define ll long long #define Pii pair<int,int> #define Pli pair<ll,int> #define ull unsigned long long #define pb push_back #define fio ios::sync_with_stdio(false);cin.tie(0) const int N=2e3+10; const int INF=0x3f3f3f3f; using namespace std; const ll mod=1e9+7; ll c[N][N]; int main() { int n,m; c[0][0]=1; for(int i=1;i<=2000;i++){ for(int j=0;j<=i;j++){ if(j==0)c[i][j]=1; else c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod; } } while(~scanf("%d %d",&n,&m)){ cout<<(c[n+m][n]*c[n+m][n]%mod-c[n+m][n-1]*c[n+m][m-1]%mod+mod)%mod<<endl; } return 0; } /* 3 1 3 1 2 1 2 2 3 1 3 */
题意:问你有多少矩阵满足各个权值为0,1,2且主对角线为0,行上权和为2的矩阵
题解:转化为邻接矩阵,行上权值为2说明各个点满足度数为2,主对角线为0说明无自环;题目转换为求给你n个点,求能构成k个环的方案数(k<=n/2)
然后就变成经典的n球成环推递推公式的问题。具体的推的步骤看这篇https://blog.csdn.net/kzn2683331518/article/details/81142483

#include<bits/stdc++.h> //CLOCKS_PER_SEC #define se second #define fi first #define ll long long #define Pii pair<int,int> #define Pli pair<ll,int> #define ull unsigned long long #define pb push_back #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0) const int N=1e5+10; const int INF=0x3f3f3f3f; const int mod=1e9+7; using namespace std; ll f[N]; int main(){ ll n,m,k; f[1]=0;f[2]=f[3]=1; while(~scanf("%lld%lld",&n,&m)){ for(ll i=4;i<=n;i++){ f[i]=((i-1)*(f[i-1]+f[i-2])-(((i-1)*(i-2)/2)%m)*f[i-3]%m+m)%m; } cout<<f[n]<<endl; } return 0; }
待补
题意:给你两个无向简单图,问你存在多少种同构
题解:next_permutation保证跑出所有的映射方案,一一将边映射过去,验证是否满足条件,用set维护不同的方案。

#include <iostream> #include <cstdio> #include <cmath> #include <algorithm> #include <map> #include <queue> #include <vector> #include <cstring> #include <iomanip> //#include <unordered_map> #include <set> #include <ctime> #include <sstream> #include <stack> //CLOCKS_PER_SEC #define se second #define fi first #define ll long long #define Pii pair<int,int> #define Pli pair<ll,int> #define ull unsigned long long #define pb push_back #define fio ios::sync_with_stdio(false);cin.tie(0) const int N=1e3+10; const int INF=0x3f3f3f3f; using namespace std; const ll mod=1e9+7; bool link[10][10],vis[10][10]; Pii p[N],P[N]; int a[N]; set<vector<bool> >s; int main() { int n,m1,m2; while(scanf("%d%d%d",&n,&m1,&m2)==3){ for(int i=1;i<=m1;i++){ cin>>p[i].fi>>p[i].se; } for(int i=1;i<=m2;i++){ int u,v;cin>>u>>v; P[i].fi=u,P[i].se=v; link[u][v]=link[v][u]=1; } for(int i=1;i<=n;i++)a[i]=i; vector<bool>vec(50); do{ int f=0; for(int i=1;i<=m1;i++){ int u=p[i].fi,v=p[i].se; if(!link[a[u]][a[v]]){ f=1; break; } vis[a[u]][a[v]]=vis[a[v]][a[u]]=1; } if(!f){ for(int i=1;i<=m2;i++){ int u=P[i].fi,v=P[i].se; if(vis[u][v]){ vec[i]=1; } } s.insert(vec); } for(int i=1;i<=m2;i++)vec[i]=0; memset(vis,0,sizeof(vis)); }while(next_permutation(a+1,a+1+n)); cout<<(int)s.size()<<endl; memset(link,0,sizeof(link)); s.clear(); } return 0; } /* 3 1 3 1 2 1 2 2 3 1 3 */
E Removal
题意:给你n个数,问你删除m个数后能有多少种不同的顺序
题解:dp,记录每个数,它前一次出现的位置。pre[i]表示当前第i个数字,它前一次出现的位置。为了保证dp不出现重复的方案,那么我们必须删除重复的区间。
首先dp[i][j], i表示当前匹配的位置,j表示删了多少数,dp[i][j]=dp[i-1][j]+dp[i-1][j-1],当前位置且删除j个数,可以从i-1位置直接转移过来,不删除第i个元素,也可以从i-1位置转移过来,并且删除i位置上的数。同时我们要减去重复的区间,也就是dp[pre[i]-1][j-(i-pre[i])],因为第i个位置和第pre[i]位置的元素相同,如果从pre[i]+1这个位置删除到i这个位置,那么整个序列都会相同

#include<bits/stdc++.h> //CLOCKS_PER_SEC #define se second #define fi first #define ll long long #define Pii pair<int,int> #define Pli pair<ll,int> #define ull unsigned long long #define pb push_back #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0) const int N=1e5+10; const int INF=0x3f3f3f3f; const int mod=1e9+7; using namespace std; ll dp[N][20]; int pre[N]; int prem[N]; int a[N]; int main(){ int n,m,k; while(~scanf("%d%d%d",&n,&m,&k)){ memset(prem,0,sizeof(prem)); memset(dp,0,sizeof(dp)); for(int i=1;i<=n;i++){ scanf("%d",a+i); pre[i]=prem[a[i]]; prem[a[i]]=i; } dp[0][0]=1; for(int i=1;i<=n;i++){ dp[i][0]=dp[i-1][0]; for(int j=1;j<=m;j++){ if(i<j)break; dp[i][j]=dp[i-1][j-1]+dp[i-1][j]; if(pre[i]&&j-(i-pre[i])>=0)dp[i][j]-=dp[pre[i]-1][j-(i-pre[i])]; dp[i][j]%=mod; dp[i][j]=(dp[i][j]+mod)%mod; } } printf("%lld\n",dp[n][m]); } return 0; }
题意:求这个sigma
题解:我们对a1...n进行排序,因为这个顺序显然不会影响答案,那么我们就要考虑每个x,当x位于ai ai+1之间,那么整个因为a1到ai为递增,所以前半段可以随便选值都不会超过x,后半段就需要容斥,展开公式。然后公式打起来太麻烦了,详细题解传送门
以及拉格朗日插值
收获杜教拉格朗日插值模版

#include <bits/stdc++.h> //CLOCKS_PER_SEC #define se second #define fi first #define ll long long #define Pii pair<int,int> #define Pli pair<ll,int> #define ull unsigned long long #define pb push_back #define fio ios::sync_with_stdio(false);cin.tie(0) const double Pi=3.14159265; const int N=8e5+5; const int mod=1e9+7; const int INF=0x3f3f3f3f; using namespace std; namespace polysum { #define rep(i,a,n) for (int i=a;i<n;i++) #define per(i,a,n) for (int i=n-1;i>=a;i--) const int D=2010; ll a[D],f[D],g[D],p[D],p1[D],p2[D],b[D],h[D][2],C[D]; ll powmod(ll a,ll b){ll res=1;a%=mod;assert(b>=0);for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;} ll calcn(int d,ll *a,ll n) { // a[0].. a[d] a[n] if (n<=d) return a[n]; p1[0]=p2[0]=1; rep(i,0,d+1) { ll t=(n-i+mod)%mod; p1[i+1]=p1[i]*t%mod; } rep(i,0,d+1) { ll t=(n-d+i+mod)%mod; p2[i+1]=p2[i]*t%mod; } ll ans=0; rep(i,0,d+1) { ll t=g[i]*g[d-i]%mod*p1[i]%mod*p2[d-i]%mod*a[i]%mod; if ((d-i)&1) ans=(ans-t+mod)%mod; else ans=(ans+t)%mod; } return ans; } void init(int M) { f[0]=f[1]=g[0]=g[1]=1; rep(i,2,M+5) f[i]=f[i-1]*i%mod; g[M+4]=powmod(f[M+4],mod-2); per(i,1,M+4) g[i]=g[i+1]*(i+1)%mod; } ll polysum(ll m,ll *a,ll n) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i] ll b[D]; for(int i=0;i<=m;i++) b[i]=a[i]; b[m+1]=calcn(m,b,m+1); rep(i,1,m+2) b[i]=(b[i-1]+b[i])%mod; return calcn(m+1,b,n-1); } ll qpolysum(ll R,ll n,ll *a,ll m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i if (R==1) return polysum(n,a,m); a[m+1]=calcn(m,a,m+1); ll r=powmod(R,mod-2),p3=0,p4=0,c,ans; h[0][0]=0;h[0][1]=1; rep(i,1,m+2) { h[i][0]=(h[i-1][0]+a[i-1])*r%mod; h[i][1]=h[i-1][1]*r%mod; } rep(i,0,m+2) { ll t=g[i]*g[m+1-i]%mod; if (i&1) p3=((p3-h[i][0]*t)%mod+mod)%mod,p4=((p4-h[i][1]*t)%mod+mod)%mod; else p3=(p3+h[i][0]*t)%mod,p4=(p4+h[i][1]*t)%mod; } c=powmod(p4,mod-2)*(mod-p3)%mod; rep(i,0,m+2) h[i][0]=(h[i][0]+h[i][1]*c)%mod; rep(i,0,m+2) C[i]=h[i][0]; ans=(calcn(m,C,n)*powmod(R,n)-c)%mod; if (ans<0) ans+=mod; return ans; } } // polysum::init(); ll pow2(ll a,ll b) { ll res=1; while(b) { if(b&1) res=res*a%mod; a=a*a%mod; b>>=1; } return res; } ll a[N],b[N]; int main(){ polysum::init(1010); int n;while(~scanf("%d",&n)){ for(int i=1;i<=n;i++){ scanf("%lld",&a[i]); } sort(a+1,a+1+n); ll now=1; ll ans=0; for(int i=1;i<=n;i++){ if(a[i]==a[i-1]){ now*=a[i];now%=mod; continue; } b[0]=0; for(int j=1;j<=n-i+1;j++){ b[j]=j*(((pow2(j,n-i+1)-pow2(j-1,n-i+1))+mod)%mod)%mod; } ll tmp=(polysum::polysum(n-i+1,b,a[i]+1)-polysum::polysum(n-i+1,b,a[i-1]+1)+mod)%mod; ans+=now*tmp%mod; ans%=mod; now*=a[i];now%=mod; } printf("%lld\n",ans); } return 0; }
题意:给你n个数,每次询问l,r,问你[1,l][r,n]有多少种不同的数字
题解:玄学莫队,离线暴力查询。或者树状数组记录一个数出现最早的位置和最晚的位置,倒着从后往前扫一遍,如果第i位置是某个数最早出现的位置,则在该数最晚出现的位置标1。如果当前i是某个询问的l,则进行[1,r]求和操作,将最晚出现的点数全部求和,那么得到的和一定是只出现的[l,r]范围内的数的个数,所有的不同的数的数目-减去只出现在里面的数就是询问的答案。
还有主席树,将n个数复制一遍,将两个区间查询,变成从只在中间询问的单区间查询

#include <iostream> #include <cstdio> #include <cmath> #include <algorithm> #include <map> #include <queue> #include <vector> #include <cstring> #include <iomanip> //#include <unordered_map> #include <set> #include <ctime> #include <sstream> #include <stack> //CLOCKS_PER_SEC #define se second #define fi first #define ll long long #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define Pii pair<int,int> #define Pli pair<ll,int> #define ull unsigned long long #define pb push_back #define fio ios::sync_with_stdio(false);cin.tie(0) const int N=1e5+10; const int INF=0x3f3f3f3f; using namespace std; const ll mod=1e9+7; inline int read(){ int x=0;char ch=getchar(); while (ch<'0'||ch>'9') ch=getchar(); while (ch<='9'&&ch>='0'){x=x*10+ch-'0';ch=getchar();} return x; } struct BIT{ int val[N]; inline int lowbit(int x){ return x&(-x); } inline void init(){ memset(val,0,sizeof(val)); } inline void add(int x,int d){ while(x<N){ val[x]+=d; x+=lowbit(x); } } inline int query(int x){ int ans=0; while(x){ ans+=val[x]; x-=lowbit(x); } return ans; } inline int Q(int l,int r){ return query(r)-query(l-1); } }T; int l[N],r[N]; int a[N]; int ans[N]; vector<int>L[N]; vector<pair<Pii,int> >Q[N]; int main(){ int n,m; while(~scanf("%d%d",&n,&m)){ int tot=0; T.init(); memset(l,0,sizeof(l)); for(int i=1;i<=n;i++){ a[i]=read(); if(!l[a[i]])l[a[i]]=i,tot++; r[a[i]]=i; } for(int i=1;i<=n;i++){ if(l[i])L[l[i]].pb(r[i]); } for(int i=1;i<=m;i++){ int x=read()+1,y=read()-1; if(x>y)ans[i]=tot; else Q[x].pb({{x,y},i}); } for(int i=n;i>=0;i--){ for(int j=0;j<(int)L[i].size();j++){ T.add(L[i][j],1); } for(int j=0;j<(int)Q[i].size();j++){ ans[Q[i][j].se]=tot-T.query(Q[i][j].fi.se); } L[i].clear(); Q[i].clear(); } for(int i=1;i<=m;i++){ printf("%d\n",ans[i]); } } return 0; }

#include <iostream> #include <cstdio> #include <cmath> #include <algorithm> #include <map> #include <queue> #include <vector> #include <cstring> #include <iomanip> //#include <unordered_map> #include <set> #include <ctime> #include <sstream> #include <stack> //CLOCKS_PER_SEC #define se second #define fi first #define ll long long #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define Pii pair<int,int> #define Pli pair<ll,int> #define ull unsigned long long #define pb push_back #define fio ios::sync_with_stdio(false);cin.tie(0) const int N=1e5+10; const int INF=0x3f3f3f3f; using namespace std; const ll mod=1e9+7; int a[N]; int cnt[N]; int n,m; int L=1,R=0; struct node { int l,r,id; }Q[N]; int ans[N];int pos[N]; int vis[N]; int tot=0; bool cmp(node x,node y){ if(pos[x.l]==pos[y.l]){ return x.r<y.r; } return pos[x.l]<pos[y.l]; } void add(int x){ vis[a[x]]++; if(vis[a[x]]==cnt[a[x]])tot++; } void del(int x){ if(vis[a[x]]==cnt[a[x]])tot--; vis[a[x]]--; } inline int read(){ int x=0;char ch=getchar(); while (ch<'0'||ch>'9') ch=getchar(); while (ch<='9'&&ch>='0'){x=x*10+ch-'0';ch=getchar();} return x; } int main(){ fio; while(~scanf("%d %d",&n,&m)){ memset(cnt,0,sizeof(cnt)); memset(vis,0,sizeof(vis)); L=1,R=0; tot=0; int sz=1000; int pp=0; for(int i=1;i<=n;i++){ a[i]=read(),cnt[a[i]]++,pos[i]=i/sz; if(cnt[a[i]]==1)pp++; } for(int i=1;i<=m;i++){ Q[i].l=read();Q[i].r=read(); Q[i].l++; Q[i].r--; Q[i].id=i; } sort(Q+1,Q+1+m,cmp); for(int i=1;i<=m;i++){ if(Q[i].l>Q[i].r){ ans[Q[i].id]=pp; continue; } while(L<Q[i].l){ del(L); L++; } while(L>Q[i].l){ add(L-1); L--; } while(R<Q[i].r){ R++; add(R); } while(R>Q[i].r){ del(R); R--; } ans[Q[i].id]=pp-tot; } for(int i=1;i<=m;i++)printf("%d\n",ans[i]); } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号