CodeForces - 633 H Fibonacci-ish II(莫队+线段树）

题意：给你一个长为n的序列，给你一个mod，再给你q次询问，每次区间查询P(a) = a1·F1 + a2·F2 + ... + an·Fn         F为对应的斐波那契数列，a1为以排好序且不重复的区间内的数

参考博客：https://blog.csdn.net/zearot/article/details/50850792

 

题解：首先对这道题目我们能够想到用莫队处理区间的查询，那么我们只要想办法把莫队的左右区间扩展和收缩解决就可以，那么怎么解决下一个出现的ai是第几大，以及比ai要大的数后移（或前移）的操作就需要用到线段树的维护，区间维护要移动的距离，正数表示向右，负数表示向左。

 

斐波那契的一个公式F[i-1]*F[k]+F[i]*F[k+1]=F[i+k]，所以只要每次维护两个值，一个是第一行的值，一个是第二行的值，线段树维护要移动的距离，

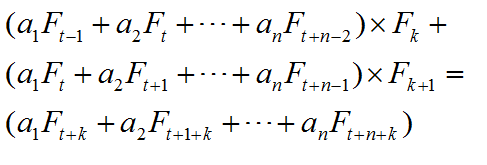（图是我盗的，盗自上面的博客）

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <queue>
#include <vector>
#include <cstring>
#include <iomanip>
#include <set>
#include<ctime>
#include<unordered_map>
//CLOCKS_PER_SEC
#define se second
#define fi first
#define ll long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define Pii pair<int,int>
#define Pli pair<ll,int>
#define ull unsigned long long
#define pb push_back
#define fio ios::sync_with_stdio(false);cin.tie(0)
const int N=3e4+10;
const ull base=163;
const int INF=0x3f3f3f3f;
using namespace std;
int a[N];
struct node {
    int l,r,id;
}Q[N];
int pos[N];
int L=1,R=0;
int ans=0;
int res[N];
int n,q,m;
int mm=1;//离散化后的个数
int fib[N<<1];
int rnk[N];//记录去重后并且排序的a[i]
int rnkA[N];//记录每个a[i]的第几大
int mp[N];//记录区间内有多少个a[i]
int V[N<<2],VL[N<<2],S[N<<2];//S是记录了区间要移动的长度 正数为向右，负数为向左
bool cmp(node x,node y){
    if(pos[x.l]==pos[y.l])return x.r<y.r;
    return pos[x.l]<pos[y.l];
}
void init(){//离散化
    sort(rnk+1,rnk+1+n);
    for(int i=2;i<=n;i++){//去重
        if(rnk[i-1]!=rnk[i]){
            rnk[++mm]=rnk[i];
        }
    }
    for(int i=1;i<=n;i++){//离散后为得到每个a[i]是第几大而进行二分
        int l=1,r=mm,ans = 0;
        while(l<=r){
            int mid=(l+r)>>1;
            if(rnk[mid]<=a[i]){
                l=mid+1;
                ans=mid;
            }
            else r=mid-1;
        }
        rnkA[i]=ans;
    }
}
//接下来所有的操作都是在1--mm这个区间内进行线段树操作
void shift(int rt,int s){
    int l=(VL[rt]*fib[mm+s]+V[rt]*fib[mm+s+1])%m;
    int r=(VL[rt]*fib[mm+s-1]+V[rt]*fib[mm+s])%m;
    V[rt]=l;
    VL[rt]=r;
}
void pushup(int rt){
    V[rt]=(V[rt<<1]+V[rt<<1|1])%m;
    VL[rt]=(VL[rt<<1]+VL[rt<<1|1])%m;
}

void pushdown(int rt){
    if(S[rt]){
        S[rt<<1]+=S[rt];
        S[rt<<1|1]+=S[rt];
        shift(rt<<1,S[rt]);
        shift(rt<<1|1,S[rt]);
        S[rt]=0;
    }
}

void move(int x,int l,int r,int rt){
    if(l==r){
        V[rt]=VL[rt]=0; 
        return ;
    }
    pushdown(rt);
    int m=(l+r)>>1;
    if(x<=m){
        move(x,lson);
        S[rt<<1|1]--;
        shift(rt<<1|1,-1);
    }
    else move(x,rson);
    pushup(rt);
}

void Insert(int x,int l,int r,int rt){
    if(l==r){
        VL[rt]=rnk[l]%m*fib[mm+S[rt]]%m;
        V[rt]=rnk[l]%m*fib[mm+S[rt]+1]%m;
        return ;
    }
    int m=(l+r)>>1;
    pushdown(rt);
    if(x<=m){
        Insert(x,lson);
        S[rt<<1|1]++;
        shift(rt<<1|1,1);
    }
    else Insert(x,rson);
    pushup(rt);
}

void del(int x){
    mp[rnkA[x]]--;
    if(mp[rnkA[x]]==0)move(rnkA[x],1,mm,1);
}

void add(int x){
    mp[rnkA[x]]++;
    if(mp[rnkA[x]]==1)Insert(rnkA[x],1,mm,1);
}

void getfib(){
    fib[mm]=0;
    fib[mm+1]=1;
    for(int i=2;i<=mm;i++)fib[mm+i]=(fib[mm+i-1]+fib[mm+i-2])%m;
    for(int i=1;i<=mm;i++)fib[mm-i]=(fib[mm-i+2]-fib[mm-i+1]+m)%m;
}

int main(){
    scanf("%d%d",&n,&m);
    int sz=sqrt(n);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        pos[i]=i/sz;
        rnk[i]=a[i];
    }
    init();
    getfib();
    scanf("%d",&q);
    for(int i=1;i<=q;i++){
        scanf("%d%d",&Q[i].l,&Q[i].r);
        Q[i].id=i;
    }
    sort(Q+1,Q+1+q,cmp);
    for(int i=1;i<=q;i++){
        while(L>Q[i].l){
            L--;
            add(L);
        }
        while(L<Q[i].l){
            del(L);
            L++;
        }
       while(R<Q[i].r){
            R++;
            add(R);
        }
        while(R>Q[i].r){
            del(R);
            R--;
        }
        res[Q[i].id]=V[1];
    }
    for(int i=1;i<=q;i++){
        printf("%d\n",res[i]);
    }
    return 0;
}