K近邻法与kd树
K近邻法与kd树
一、k近邻算法
输入:训练数据集
\[T = \{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\} \]其中,\(x_i \in R^n\) 为实例的特征向量,\(y_i \in Y = {c_1,c_2,c_3,..,c_k}\)为实例类别,\(i=1,2,3,..N\),实例特征向量\(x\).
输出:实例特征向量所属的类
(1) 根据给定的距离度量,在训练集\(T\)中找出与\(x\)最邻近的\(k\)个点,涵盖这\(k\)个点的\(x\)的邻域记作\(N_k(x)\).
(2) 在\(N_k(x)\)中根据分类决策规则(如多数表决)决定\(x\)的类别\(y\)。
\[y = \mathop{argmax}_{c_j} \sum_{x_i\in N_k(x)} I(y_i=C_j) \]
k近邻算法没有显式的学习过程。
二、k近邻模型
k近邻模型由三个基本要素组成——距离度量,k值选择,分类决策规则
2.1 距离度量
闵可夫斯基距离公式:
当p = 2 时,公式称为欧式距离。
当p = 1时,公式称为曼哈顿距离。
当p = \(\infin\)时,它时各个坐标的最大值,即:\(L_{\infin}(x_i,x_j) = \mathop{max}_l|x_i^{(l)} - x_j^{(l)}|\)
2.2 k值的选择
k值选择越小,对噪声越敏感,越容易造成过拟合
2.3 分类决策规则
一般采用多数表决规则(majority voting rule)
三、k近邻法的实现:kd树
但我们使用k近邻算法时,其中最耗时的就是对k近邻的搜索,当我们需要比较每一个训练数据点与所求样本之间的距离,如果是线性搜索,那么当特征空间的维数和训练数据量非常大时,这就变成了k近邻法的鸡肋了。
为了提高k近邻搜索的效率,我么可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数。这里我们就要用到kd树的方法。(这里的k指的是k维空间)
3.1 构造kd树
kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构,kd树是二叉树,表示对k维空间的一个划分。构造kd树相当于不断的用垂直于坐标轴的超平面将k维空间切分,构成一系列的k维超矩形空间。
构造kd树的算法如下:
输入:k维空间数据集\(T={x_1,x_2,...,x_N}\)其中$ x_i = (x_i{(1)},x_i,...,x_i^{(k)} )$
输出:kd树
(1)开始:构造根结点,根结点对应于包含T的k维空间的超矩形区域。
选择\(x^{(1)}\)为坐标轴,以T中所有实例的\(x^{(1)}\)坐标的中位数为切分点,将根节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴\(x^{(1)}\)垂直的超平面实现。
由根结点生成深度为1的左右子结点:左子结点对应坐标\(x^{(1)}\)小于切分点的子区域,右子结点对应于坐标\(x^{(1)}\)大于切分点的子区域。
(2) 重复:对深度为\(j\) 的结点,选择\(x^{(l)}\) ,\(l=j(mod\ k)+1\) 以该结点的区域中所有实例的\(x^{(l)}\)的中位数为切分点,将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。
由根结点生成深度为\(j+1\)的左右子结点:左子结点对应坐标\(x^{( l )}\)小于切分点的子区域,右子结点对应于坐标\(x^{(l)}\)大于切分点的子区域。
(3)直到两个子区域没有实例存在时停止,从而形成kd树的区域划分。
代码(简化代码实现,只实现二维的)
先对kd树和结点进行定义
class KDT(object):
def __init__(self):
self.head = None
class KDTNode(object):
def __init__(self, parent, value, axis):
self.left = None
self.right = None
self.parent = parent
self.value = value
self.axis = axis
self.isVisit = False #搜索时记录是否被访问过
下面是kd树的构造过程和其用到的工具方法:
def handleData(data, idx):
'''
将数据根据idx维度的中位数进行划分
:param data: 要划分的数据
:param idx: 在数据的哪个维度上进行划分
:return: 作为划分结点的med ,左子树数据left,右子树数据right
'''
tmp = data[:, idx]
medI = np.median(tmp)
no = (np.abs(tmp - medI)).argmin()
medI = data[no, idx]
med = data[no]
data = np.delete(data, no, axis=0)
left = data[data[:, idx] < medI]
right = data[data[:, idx] >= medI]
return med, left, right
def builtNode(data, parent, idx):
'''
构造kd树的结点
:param data: 输入的数据
:param parent: 父节点
:param idx: 在idx维度上进行划分
:return:
'''
# 将数据分为idx维度上的中间节点,左部分,右部分
med, left, right = handleData(data, idx)
node = KDTNode(parent=parent, value=med, axis=idx)
if (left.size != 0):
node.left = builtNode(left, node, 1 - idx)
if (right.size != 0):
node.right = builtNode(right, node, 1 - idx)
return node
def builtKDT(data):
'''
构造kd树
:param data: 输入的数据
:return:
'''
kdt = KDT()
kdt.root = builtNode(data, None, 0)
return kdt
def printKDT(kdt):
'''
二叉树的先序输出
:param kdt:
:return:
'''
printNode(kdt.root)
def printNode(node):
print('结点数据:{},划分维度:{}'.format(node.value, node.axis))
if node.left != None:
printNode(node.left)
if node.right != None:
printNode(node.right)
data = np.array([[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]])
kdt = builtKDT(data2)
printKDT(kdt)
上述代码的结果截图如下:
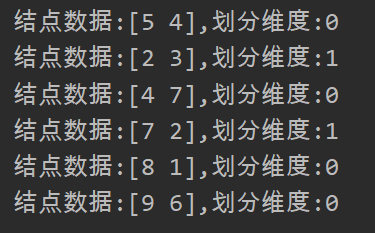
3.2 搜索kd树
下面介绍如何利用kd树进行最近邻搜索(k=1):给定一个 目标点,首先找到代表目标点区域的叶节点,然后从该叶节点出发,依次回退到父节点,不断查找与目标节点最邻近的节点,当确定不可能存在更近的节点时终止。
输入:已构造的kd树,目标点x
输出: x的最近邻
(1) 在kd树中找出包含目标点x区域的叶节点:从根节点出发,递归的向下访问kd数。在kd树的每层中,通过在划分依据的维度idx上进行比较,比当前访问节点小,就向左子树走,反之就向右子树走。
(2) 以叶节点为“当前最近点”。
(3) 递归地向上回退,在每个节点处进行以下操作:
(a)如果当前结点与目标结点的距离比已知的最邻近结点少,则将当前结点标记为最邻近节
点。
(b) 检查当前结点的另一个子树是否有更接近的数据点。具体操作为:已目标点为圆心,以与最近邻点的距离为半径画圆,如果该圆与另一个子树所代表的区域相交,则在另一个子树上执行kd树的最近邻搜索。然后继续回退到父节点。
(4) 当回退到根节点时,搜索结束。最终记录的最近邻点即为所求点。
def findleaf(root, x):
'''
根据kd树,找到x对应的叶节点
:param root: kd树的根节点
:param x: 目标节点
:return: 叶节点
'''
axis = root.axis
leaf = root
if (x[axis] < root.value[axis]) & (root.left != None):
leaf = findleaf(root.left, x)
if (x[axis] >= root.value[axis]) & (root.right != None):
leaf = findleaf(root.right, x)
return leaf
def nearstNeighborSearch(node, x, curDis, cur, searchSibling):
'''
递归的查找最近邻点
:param node:
:param x:
:param curDis:
:param cur:
:param searchSibling:
:return:
'''
if node.isVisit:
return curDis, cur
node.isVisit = True
dis = np.sqrt(np.sum((node.value - x) ** 2))
if dis < curDis:
curDis = dis
cur = node
if (searchSibling == 1) & (node.left != None):
tmpDis, tmp = nearstNeighbor(node.left, x, curDis=curDis, cur=cur)
if tmpDis < curDis:
curDis = tmpDis
cur = tmp
if (searchSibling == 2) & (node.right != None):
tmpDis, tmp = nearstNeighbor(node.right, x, curDis=curDis, cur=cur)
if tmpDis < curDis:
curDis = tmpDis
cur = tmp
if node.parent != None:
axis = node.parent.axis
tmpDis, tmp = 0, None
if (x[axis] < node.parent.value[axis]) & (node.parent.value[axis] - x[axis] < curDis):
tmpDis, tmp = nearstNeighborSearch(node.parent, x, curDis, cur, 2)
elif (x[axis] >= node.parent.value[axis]) & (x[axis] - node.parent.value[axis] < curDis):
tmpDis, tmp = nearstNeighborSearch(node.parent, x, curDis, cur, 1)
else:
tmpDis, tmp = nearstNeighborSearch(node.parent, x, curDis, cur, 0)
if tmpDis < curDis:
curDis = tmpDis
cur = tmp
return curDis, cur
def nearstNeighbor(root, x, curDis=np.inf, cur=None):
leaf = findleaf(root, x)
curDis, cur = nearstNeighborSearch(leaf, x, curDis, cur, 0)
return curDis, cur
data = np.array([[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]])
kdt = builtKDT(data)
printKDT(kdt)
x = np.array([4, 5])
nearestDis, nearestNode = nearstNeighbor(kdt.root, x, curDis=np.inf, cur=None)
print(nearestDis, nearestNode.value) #输出最短距离 最近邻点
运行的结果如下:

详细代码:github
如果实例点是随机分布的,kd树搜索的平均计算复杂度是\(O(logN)\).



