熵、交叉熵、KL散度、JS散度

熵、交叉熵、KL散度、JS散度

一、信息量

事件发生的可能性大，信息量少；事件发生的可能性小，其信息量大。 即一条信息的信息量大小和它的不确定性有直接的关系，比如说现在在下雨，然后有个憨憨跟你说今天有雨，这对你了解获取天气的信息没有任何用处。但是有人跟你说明天可能也下雨，这条信息就比前一条的信息量大。可以看出信息量的大小与事件发生的可能性成反比。

\[\begin{align} p\left(x\right) &= Pr(X=x),x \in \chi \notag \\ I(x) &= - \log(p(x)) \tag{1} \end{align} \]

\(I(x)\)称为随机变量X的自信息，描述的是随机变量的某个事件（X = \(x\)）发生所带来的信息量。这里可以稍微理解一下为什么使用\(log\) :例如两个相互独立的事件\(x,y\),因为两者相互独立所以两个事件带来的信息量为\(I(x)+I(y)\) ,而两个事件同时发生的概率是\(p(x,y) = p(x)p(y)\)。\(log\)函数就满足这两个式子，其中\(log\)的基数可以任意，常用的是2(二进制编码),\(e\)。

二、熵

从信息量的公式可以看出，当一个事件的发生概率为\(p(x)\) 时，它的信息量就是\(-log(p(x))\)。那么我们将这个事件的所有可能发生的结果都罗列出来，求的该事件信息量的期望(信息量的算术平均)：

\[H(x) = - \sum_{i=1}^{n}p(x_i)log(p(x_i)) \tag{2} \]

熵其实表示的是一种混乱程度，其最初就是从化学领域引入到信息论当中的，随机变量的取值越多，状态数也就越多，也越混乱。就比如你获取信息的来源越多，信息量越大，你脑子里就越乱，头大。

三、KL散度(相对熵)

对于同一个随机变量有两个单独的概率分布，我们可以使用KL散度(Kullback-Leibler divergence)来衡量两个分布的差异。在机器学习的损失函数的计算中，我们可以假设\(P\)为样本的真实分布，\(Q\)用来表示模型所预测的分布，使用KL散度来衡量两个分布之间的差异，

\[D_{KL}(p||q) = \sum_{i=1}^n p(x_i)log(\frac{p(x_i)}{q(x_i)}) \tag{3} \]

当\(p(x_i)\)越接近\(q(x_i)\)，\(D_{KL}(p||q)\)就越小，极端情况下\(p(x_i)=q(x_i)\)时，\(D_{KL}=0\)。即损失函数越小，模型预测越准确。KL散度又称为KL距离，但从公式中可以看出其不满足：

1. 对称性，\(D_{KL}(p||q)!=D_{KL}(q||p)\)
2. 三角不等式(两边之和大于第三边，两边之差小于第三边)

四、交叉熵

交叉熵是从相对熵中提取出来的，我们可以对（3）式进行展开：

\[\begin{align} D_{KL}(p||q) &= \sum_{i=1}^np(x_i)log(\frac{p(x_i)}{q(x_i)}) \notag\\ &=\sum_{i=1}^np(x_i)(logp(x_i)-logq(x_i)) \notag\\ &=\sum_{i=1}^n[p(x_i)logp(x_i)-p(x_i)logq(x_i)] \notag\\ &=\sum_{i=1}^np(x_i)logp(x_i)-\sum_{i=1}^np(x_i)logq(x_i)\tag{4} \end{align} \]

而交叉熵就等于

\[H(p,q) = -\sum_{i=1}^np(x_i)logq(x_i) \tag{5} \]

为（4）式的后半部分。

在深度学习的损失评估中，相对熵(KL散度)可以比较两个分布(真实分布和预测结果的分布)的差异。当训练数据给定，其真实分布是确定的。比如多分类问题中，一张图片的结果是猫，无论模型怎么优化，其预测结果是不确定的，但真实的label就是猫。所以在\(D_{KL}\)中的\(\sum_{i=1}^np(x_i)logp(x_i)\)是个常数，它对于损失函数的比较和梯度下降没有帮助。此时KL散度于交叉熵的作用是一样的，为了减少计算量可以直接用交叉熵作为其损失函数。

五、为什么使用交叉熵而不是均方差

从上面的分析我们可以看出KL散度(交叉熵也是一样的)并不是对称的，这样训练过程中对训练数据的顺序不同可能会造成训练时间的差异（可以想象一下在几何意义上距离相同的两个训练数据点对梯度的贡献不同，于是对这两个数据点的计算顺序不同可能会对梯度下降的快慢造成影响）。

这里我们从梯度消失的角度来进行分析。我们已二分类问题为例，在二分类问题中我们在输出层使用的是sigmod函数：

\[\sigma(z) = \frac{1}{1+e^{-z}} \]

对它进行求导为：

\[\sigma'(z) =\frac{1}{1+e^{-z}} \cdot \frac{e^{-z}}{1+e^{-z}}=\sigma(z)(1-\sigma(z))\tag{6} \]

从（6）式中可以看出当\(\sigma(z)\)接近于0或者是1时，\(\sigma(z)\)产生的梯度接近于0，发生梯度弥散。

我们先描述一下模型的结构：

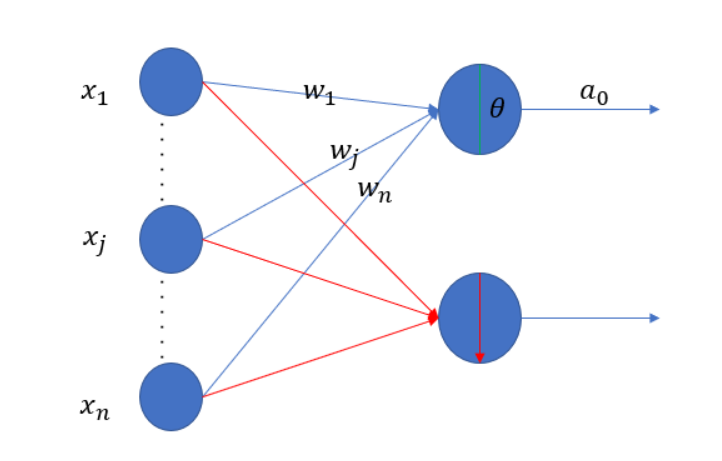
然后就是均方差和交叉熵的公式来计算loss function：

\[\begin{align} MSE: L(a,y) &= \sum_i\frac{1}{2}(a_i-y_i)^2 \tag{7}\\ CROSS\ ENTROPY: L(a,y)&=y_ilog(a_i)+(1-y_i)log(1-a_i) \tag{8} \end{align} \]

模型的前向传播为：

\[a_0 = \theta(\sum_jw_{ij}\cdot x_{ij}) \\ \]

1. 应用均方差的反向传播过程：

   \[\begin{align} \frac{\partial L}{\partial a_0} &= a_0-y_0 \notag\\ \frac{\partial a_0}{\partial w_1} &= a_0(1-a_0)x_0(从(6)式可得) \notag\\ \frac{\partial L}{\partial w_1} &= a_0(1-a_0)x_0(a_0-y_0) \tag{9} \end{align} \]

2. 应用交叉熵的反向传播过程：

\[\begin{align} \frac{\partial L}{\partial a_0} &= -\frac{y_0}{a_0}+\frac{1-y_0}{1-a_0} \notag \\ \frac{\partial a_0}{\partial w_1} &= a_0(1-a_0)x_0(从(6)式可得) \notag\\ \frac{\partial L}{\partial w_1} &=(a_0-y_0)x_0 \tag{10} \end{align} \]

这里只从\(w_1\)的更新来说明问题，从(9)和(10)式可以看出但\(a_0\)取值为0或者1时，MSE容易造成梯度消失，而(10)式可以在一定程度上抑制这种影响。

六、JS散度

JS散度也是用于度量两个概率分布的相似度，其解决了KL散度不对称的缺点。

\[JS(p||q) = \frac{1}{2}KL(p||\frac{p+q}{2})+\frac{1}{2}KL(q||\frac{p+q}{2}) \]