算法:拓扑排序
算法:拓扑排序
什么是拓扑排序
其实在写这篇博客的时候,我也是以一个学习者的角度出发的,目的就是想让自己理解和初步掌握拓扑排序。
维基百科的定义如下:
在计算机科学领域,有向图顶点的线性排序就是其拓扑排序,例如,图形的顶点可以表示要执行的任务,并且边可以表示一个任务必须在另一个任务之前执行的约束; 在这个应用中,拓扑排序只是一个有效的任务顺序。当且仅当图形没有定向循环,即如果它是有向无环图(DAG),则拓扑排序是可能的。 任何 DAG 具有至少一个拓扑排序,并且已知这些算法用于在线性时间内构建任何 DAG 的拓扑排序。
在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序(英语:Topological sorting)。
- 每个顶点出现且只出现一次;
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
比如在下图中,当然首先必须是有向无环图,从1出发到达,拓扑序列可以为1,3,2,5,4。
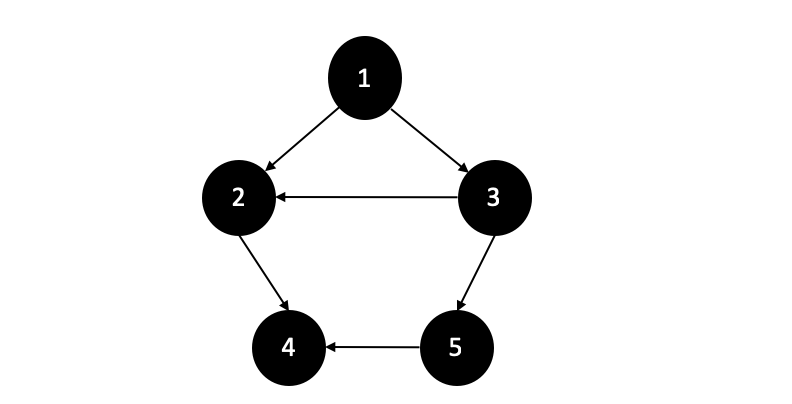
我们在写有向无环图的拓扑排序时遵循一种常用的方法:
- 从 DAG 图中选择一个 没有前驱(即入度为0)的顶点并输出。
- 从图中删除该顶点和所有以它为起点的有向边。
- 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
拓扑排序的应用
拓扑排序通常用来“排序”具有依赖关系的任务。
比如,如果用一个DAG图来表示一个课程修读关系图,其中每个顶点表示学期中的一个课程,用有向边 表示在学习务课程B 之前必须先学习课程 A。故在这个体系中,任意两个课程要么具有确定的先后关系,要么是没有关系,绝对不存在互相矛盾的关系(即环路)。
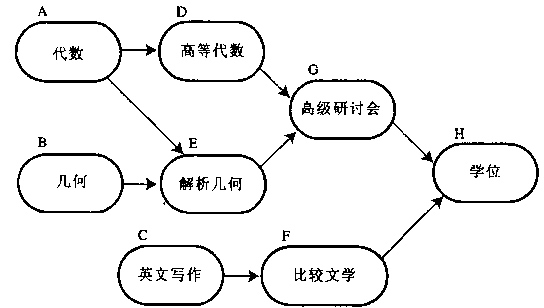
再举一例,比如我们早上起来穿衣服,也遵循一种流程:
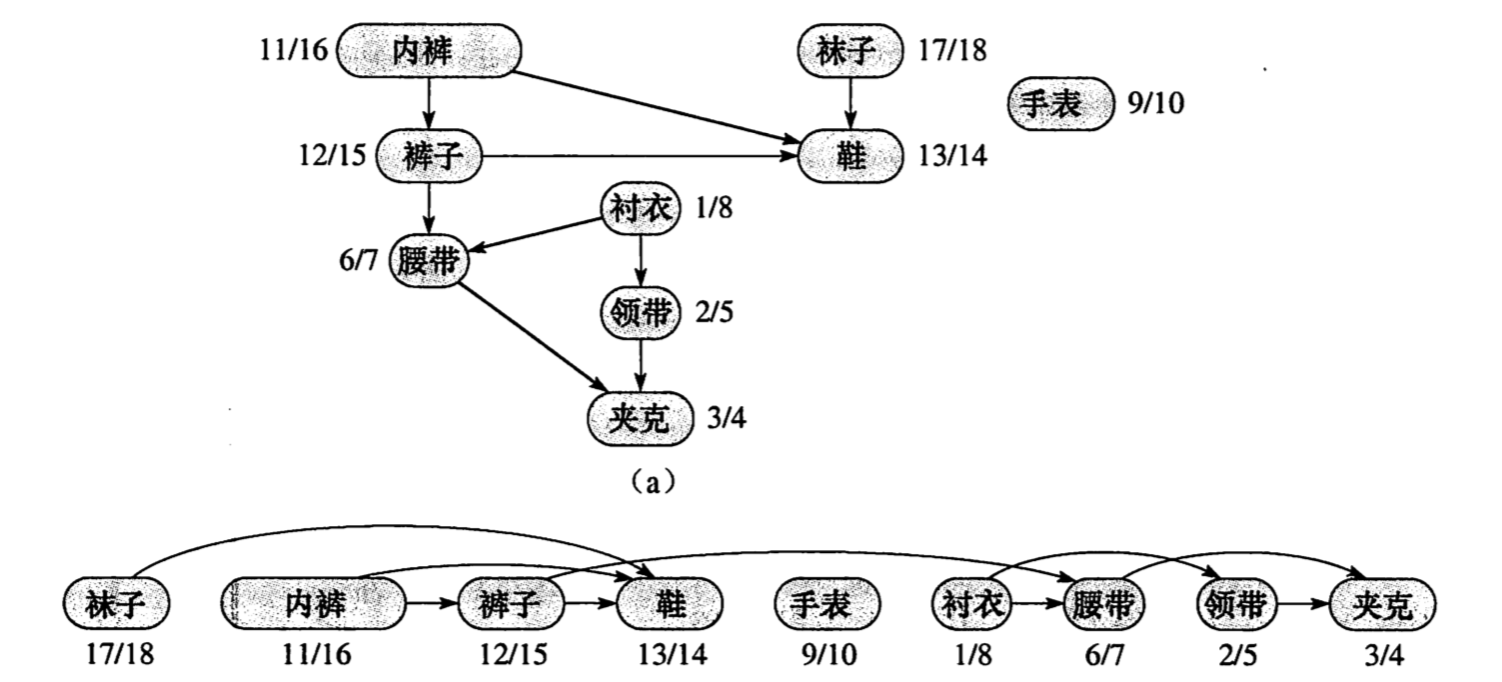
拓扑排序的实现
思路分析
下面代码写的非常好。认真阅读你就会发现拓扑排序是基于DFS的,只是加入了一个栈来保存结果。
我们首先知道拓扑排序结果是一个线性排列,这说明了一定存在两类点,一类是入度为0,一类是出度为0。(入度为0指的是只想它的边为0,出度指的是它不指向任何边)。
下图演示了一个从0度点出发的一个DFS树:

首先2节点的邻接顶点是1和3,由于我们是DFS,它就会一条路走下去,所以先走左边,即到达1号节点,然后1号节点的邻接顶点是4,所以接下来箭头指向4,4是一个出度为0的节点,它没有邻接顶点,所以不用再往下递归,把4直接保存到栈中。接着返回到1节点,把1压入栈中,然后返回到2节点,接着走右边这条路,到达3号节点,接着从3号节点的邻接顶点出发,但是都已经访问过了,所以返回3后,直接把3压入栈中,最后返回2,把2压入栈中。
所以最后的结果就是2,3,1,4。
但我们还是简单思考一下为什么这样子的测量就把拓扑排序搞出来了?我们可以这样想,无论我们从哪个节点出发,只要他指向其他顶点,我们就要去处理那些顶点,所以这个节点一定是被后压入栈中的,也就是最先被访问的,那些DFS深入到最后的节点,已经不指向任何顶点,所以他是最后被访问的。其实我们理解到这里就可以了。
Java实现
import java.io.*;
import java.util.*;
// 这个类代表一个使用邻接列表表示的有向图
class Graph
{
private int V; // No. of vertices
private LinkedList<Integer> adj[]; // Adjacency List
//构造方法
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
// 添加一个边到图中
void addEdge(int v,int w) { adj[v].add(w); }
// 被拓扑排序调用的DFS函数
void topologicalSortUtil(int v, boolean visited[],
Stack stack)
{
// 标记当前节点为已访问.
visited[v] = true;
Integer i;
// 递归访问它的所有邻接顶点
Iterator<Integer> it = adj[v].iterator();
while (it.hasNext())
{
i = it.next();
if (!visited[i])
topologicalSortUtil(i, visited, stack);
}
// 把当前节点加入存放结果的栈中
stack.push(new Integer(v));
}
// 拓扑排序
void topologicalSort()
{
Stack stack = new Stack();
// 标记所有节点为未访问
boolean visited[] = new boolean[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// Call the recursive helper function to store
// Topological Sort starting from all vertices
// one by one
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i, visited, stack);
// 打印结果栈的内容
while (stack.empty()==false)
System.out.print(stack.pop() + " ");
}
public static void main(String args[])
{
Graph g = new Graph(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
System.out.println("Following is a Topological " +
"sort of the given graph");
g.topologicalSort();
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号