算法：并查集

算法：并查集

快速掌握

理解算法

　　在计算机科学中，并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

  • Find：确定元素属于哪一个子集。这个确定方法就是不断向上查找找到它的根节点，它可以被用来确定两个元素是否属于同一子集。
  • Union：将两个子集合并成同一个集合。

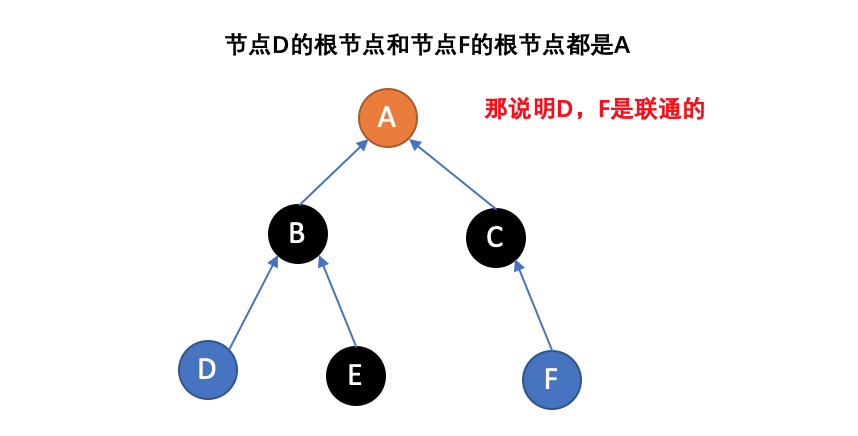
　　由于支持这两种操作，一个不相交集也常被称为联合-查找数据结构（union-find data structure）或合并-查找集合（merge-find set）。其他的重要方法，MakeSet，用于建立单元素集合。有了这些方法，许多经典的划分问题可以被解决。

　　为了更加精确的定义这些方法，需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素，称为代表，以表示整个集合。接着，Find(x) 返回 x 所属集合的代表，而 Union 使用两个集合的代表作为参数。

　　

 

说明：左边是A，笔误！

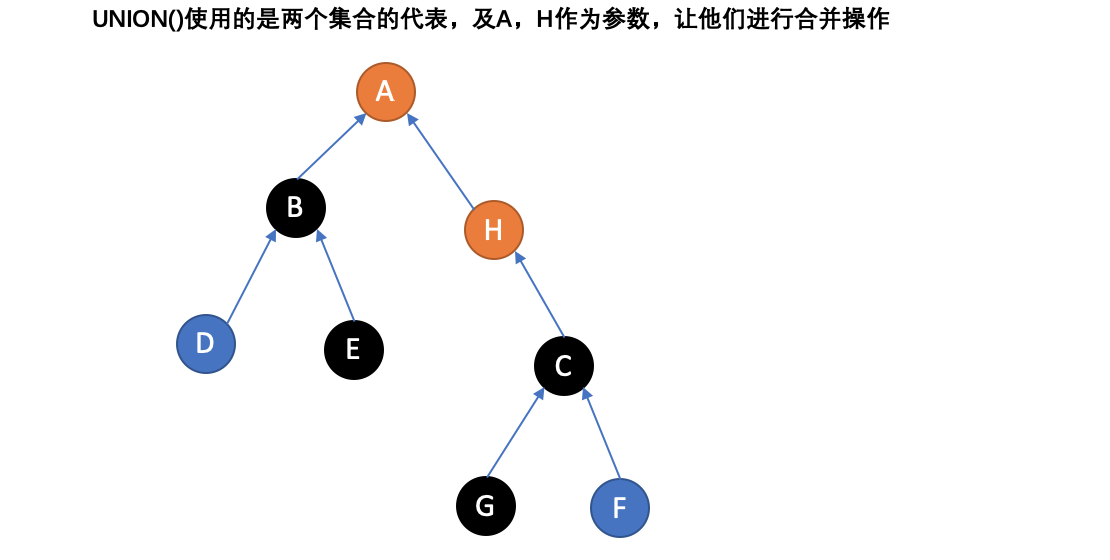
　　上图中简单演示了并查集的两个操作，一个是FIND，一个UNION。

并查集(树)

　　并查集（树）是一种将一个集合以树形结构进行组合的数据结构，如上图所示。其中每一个节点保存着到它的父节点的引用（

　　在并查集树中，每个集合的代表即是集合的根节点。

  • “查找”根据其父节点的引用向根行进直到到底树根。
  • “联合”将两棵树合并到一起，这通过将一棵树的根连接到另一棵树的根。

　　实现这样操作的伪代码如下：

 function MakeSet(x)
     x.parent := x

 function Find(x)
     if x.parent == x
        return x
     else
        return Find(x.parent)

 function Union(x, y)
     xRoot := Find(x)
     yRoot := Find(y)
     xRoot.parent := yRoot

　　这是并查集树林的最基础的表示方法，这个方法不会比链表法好，这是因为创建的树可能会严重不平衡；然而，可以用两种办法优化。

优化方法一：按秩合并

　　第一种方法，称为“按秩合并”，即总是将更小的树连接至更大的树上。因为影响运行时间的是树的深度，更小的树添加到更深的树的根上将不会增加秩除非它们的秩相同。在这个算法中，术语“秩”替代了“深度”，因为同时应用了路径压缩时（见下文）秩将不会与高度相同。单元素的树的秩定义为0，当两棵秩同为r的树联合时，它们的秩r+1。只使用这个方法将使最坏的运行时间提高至每个MakeSet、Union或Find操作、O(\log n)。

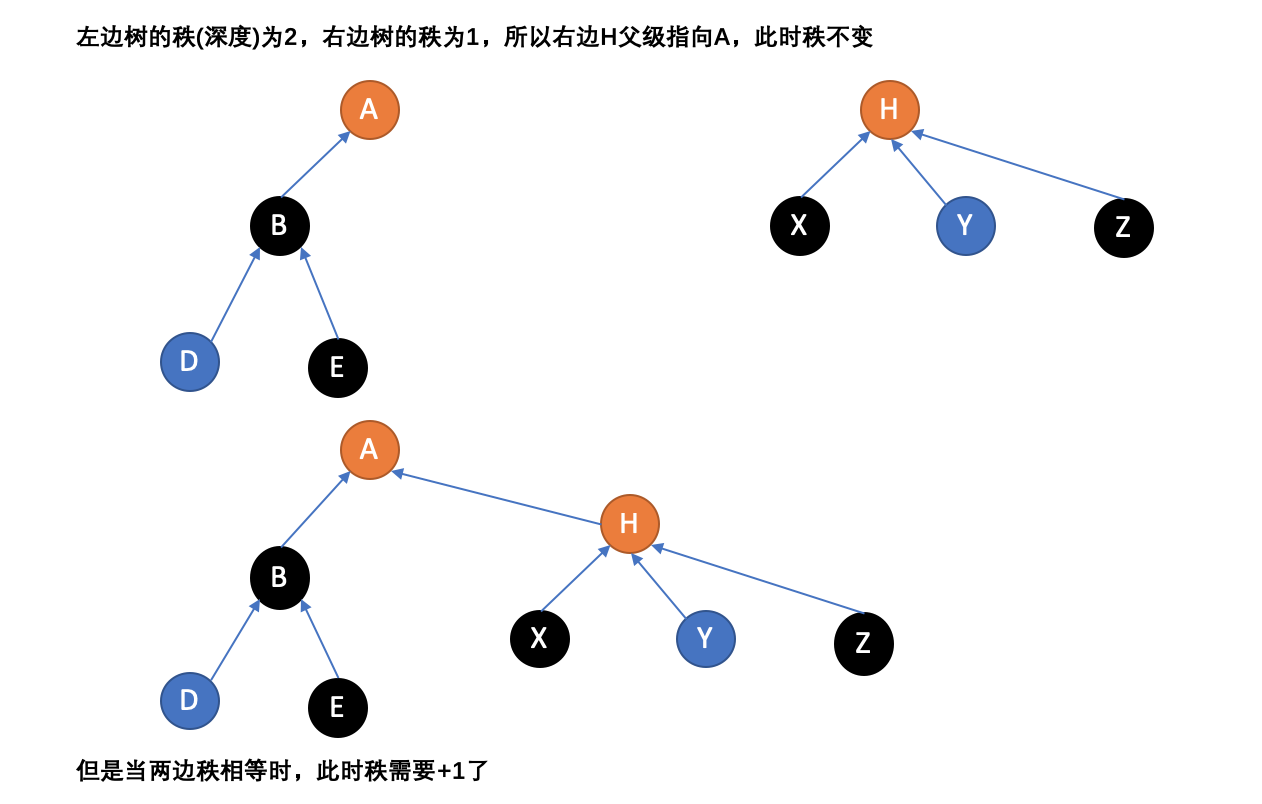
优化后的MakeSet和Union伪代码：

 function MakeSet(x)
     x.parent := x
     x.rank   := 0

 function Union(x, y)
     xRoot := Find(x)
     yRoot := Find(y)
     if xRoot == yRoot
         return

     // x和y不在同一个集合，合并它们。
     if xRoot.rank < yRoot.rank
         xRoot.parent := yRoot
     else if xRoot.rank > yRoot.rank
         yRoot.parent := xRoot
     else
         yRoot.parent := xRoot
         xRoot.rank := xRoot.rank + 1　　

优化方法二：路径压缩 

　　第二个优化，称为“路径压缩”，是一种在执行“查找”时扁平化树结构的方法。关键在于在路径上的每个节点都可以直接连接到根上；他们都有同样的表示方法。为了达到这样的效果，Find递归地经过树，改变每一个节点的引用到根节点。得到的树将更加扁平，为以后直接或者间接引用节点的操作加速。

　　

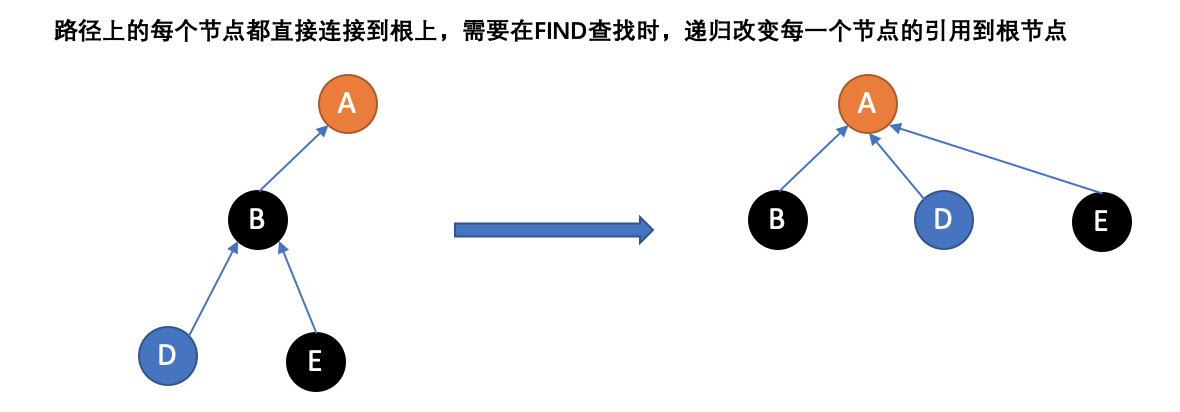
这儿是Find：

 function Find(x)
     if x.parent != x
        x.parent := Find(x.parent)
     return x.parent　　

　　这两种方法的优势互补，同时使用二者的程序每个操作的平均时间仅为O(\alpha (n))，\alpha (n)是n=f(x)=A(x,x)的反函数，其中A是急速增加的阿克曼函数。因为\alpha (n)是其的反函数，故\alpha (n)在n十分巨大时还是小于5。因此，平均运行时间是一个极小的常数。

　　实际上，这是渐近最优算法：Fredman和Saks在1989年解释了\Omega (\alpha (n))的平均时间内可以获得任何并查集。

 

并查集算法-Java实现

package search;

public class UnionFindSet {
    private int[] parents_;
    private int[] ranks_;

    public UnionFindSet(int n)
    {
        parents_ = new int[n+1];
        ranks_ = new int[n+1];
        for(int i=0;i<=n;i++)
        {
            parents_[i]=i;
            ranks_[i]=i;
        }
    }

    public boolean Union(int u,int v)
    {
        int pu = Find(u);
        int pv = Find(v);
        if(pu==pv)
            return false;
        if (ranks_[pv] > ranks_[pu])
            parents_[pu] = pv;
        else if (ranks_[pu] > ranks_[pv])
            parents_[pv] = pu;
        else {
            parents_[pv] = pu;
            ranks_[pu] += 1;
        }
        return true;
    }

    public int Find(int u)
    {
        while (parents_[u]!=u)
        {
            parents_[u]=parents_[parents_[u]];
            u=parents_[u];
        }
        return u;
    }

}

 

主要操作

合并两个不相交集合

　　操作很简单：先设置一个数组(阵列)Father[x]，表示x的“父亲”的编号。 那么，合并两个不相交集合的方法就是，找到其中一个集合最父亲的父亲（也就是最久远的祖先），将另外一个集合的最久远的祖先的父亲指向它。

void Union(int x,int y)
{
    fx = getfather(x);
    fy = getfather(y);
    if(fy!=fx)
       father[fx]=fy;
}

判断两个元素是否属于同一集合

　　仍然使用上面的数组。则本操作即可转换为寻找两个元素的最久远祖先是否相同。寻找祖先可以采用递归实现，见后面的路径压缩算法。

bool same(int x,int y)
{
   return getfather(x)==getfather(y);
}
/*返回true 表示相同根结点，返回false不相同*/
posted @ 2018-09-07 23:24  子烁爱学习  阅读(29342)  评论(3)  编辑  收藏  举报