算法:希尔排序
算法:希尔排序
快速开始
百科解释
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
-
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
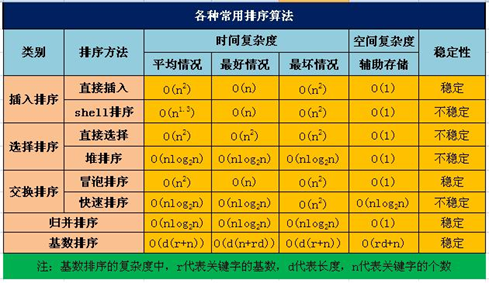
补充:各种常用排序算法的复杂度分析:
主要思想
原始的算法实现在最坏的情况下需要进行O(n2)的比较和交换。V. Pratt的书[1]对算法进行了少量修改,可以使得性能提升至O(n log2n)。这比最好的比较算法的O(n log n)要差一些。
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n2)的排序(冒泡排序或插入排序),可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据,所以小数据只需进行少数比较和交换即可到正确位置。
一个更好理解的希尔排序实现:将数组列在一个表中并对列排序(用插入排序)。重复这过程,不过每次用更长的列来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法,算法本身仅仅对原数组进行排序(通过增加索引的步长,例如是用i += step_size而不是i++)。
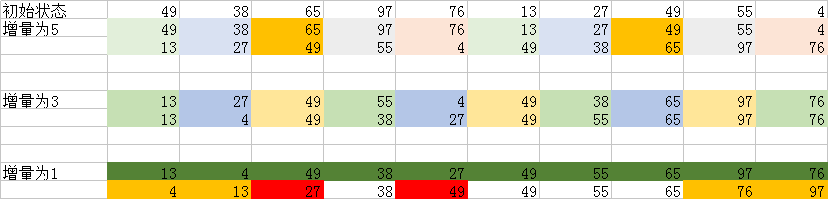
实例说明
颜色相同表示根据步长被划分到同一批次中。同一批次中的元素进行插入排序,这样一个元素很有可能将朝着最终位置前进一大步。到最后可见需排列的数据几乎已经拍好了。但是也正是由于数组元素大小及位置关系的不确定性,导致了该算法是不稳定的。
Java实现代码
package com.company.sort;
public class shellSort {
public static void main(String[] args)
{
int[] arr= { 13,14, 94, 33 ,82 ,25 ,59 ,94 ,65, 23 ,45 ,27, 73, 25, 39, 10};
shell_sort(arr);
}
public static void shell_sort(int[] arr) {
//gap 为步长...
int gap = 1, i, j, len = arr.length;
int temp;
//步长计算方式不唯一
while (gap < len / 3)
gap = gap * 3 + 1; // <O(n^(3/2)) by Knuth,1973>: 1, 4, 13, 40, 121, ...
for (; gap > 0; gap /= 3)
//步长不断缩小,最后为1
for (i = gap; i < len; i++) {
//取出第i个元素
temp = arr[i];
//从第i个元素开始,与之前每次步长为gap的元素进行比较
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
arr[j + gap] = arr[j]; //如果前者元素大于后者,则互换位置
arr[j + gap] = temp; //因为上面循环最后一次比较j仍会减gap,所以还要补偿回来gap
}
for(int num:arr)
System.out.println(num);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号