算法：字符串处理

算法：字符串处理

字符串的排列

问题描述

　　输入一个字符串，打印出该字符串中字符的所有排列。例如，输入字符串abc，则打印出由字符a、b、c所能排列出来的所有字符串abc,acb,bac,bca,cab,cba.

解决思路

　　我们求整个字符串的排列，可以分成两步，第一步求所有可能出现在第一个位置的字符，即把第一个字符与后面所有字符交换。

　　

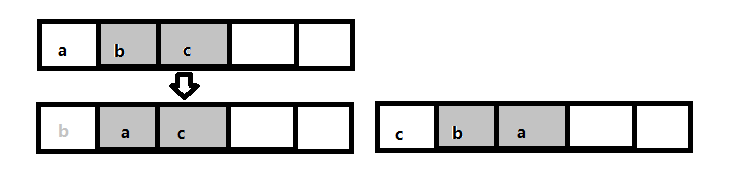
　　第二步，固定第一个字符，求后面所有字符的排列。这时仍把后面的字符分成两部分：后面的第一个字符，以及这个字符之后的所有字符。然后把第一个字符逐一和后面的字符交换。

Java实现代码

　　private static HashSet<String> resultSet = new HashSet<>();

　　public static void main(String[] args) {
        String test = "abcd";

        printStr(test,0);
        Iterator<String> it = resultSet.iterator();
        while (it.hasNext())
            System.out.println(it.next());
    }

    public static void printStr(String test,Integer ptr)
    {
        if(ptr<=test.length())
        {
            char[] chars = test.toCharArray();
            for(int i=ptr;i<chars.length;i++)
            {

                char temp = chars[i];
                chars[i]=chars[ptr];
                chars[ptr]=temp;
                resultSet.add(new String(chars));
                printStr(new String(chars),ptr+1);
            }
        }
    }

最长不含重复字符的子字符串

问题描述

　　请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。假设字符串中只还有'a'~'z'的字符。

解决思路

Java实现代码

构造回文串

问题描述

　　给定一个字符串s，你可以从中删除一些字符，使得剩下的串是一个回文串。如何删除才能使得回文串最长呢？
输出需要删除的字符个数。

解决思路

提到回文串，自然要利用回文串的特点，想到将源字符串逆转后，“回文串”（不一定连续）相当于顺序没变
求原字符串和其反串的最大公共子序列（不是子串，因为可以不连续）的长度（使用动态规划很容易求得），然后用原字符串的长度减去这个最大公共子串的长度就得到了最小编辑长度。

最大公共子序列

   最长公共子序列的结构有如下表示：

   设序列X=<x1, x2,="" …,="" xm="">和Y=<y1, y2,="" …,="" yn="">的一个最长公共子序列Z=<z1, z2,="" …,="" zk="">，则：

   1> 若 xm=yn，则 zk=xm=yn，且Zk-1是Xm-1和Yn-1的最长公共子序列； 

   2> 若 xm≠yn且 zk≠xm ，则 Z是 Xm-1和 Y的最长公共子序列；

   3> 若 xm≠yn且 zk≠yn ，则 Z是 X和 Yn-1的最长公共子序列；

   其中Xm-1=<x1, x2,="" …,="" xm-1="">，Yn-1=<y1, y2,="" …,="" yn-1="">，Zk-1=<z1, z2,="" …,="" zk-1="">。

<x1, x2,="" …,="" xm-1=""><y1, y2,="" …,="" yn-1=""><z1, z2,="" …,="" zk-1=""> 

图片演示

 

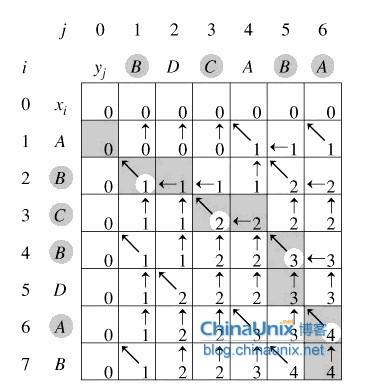
C++实现最大公共子序列

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
const int MAX = 1001;
int MaxLen[MAX][MAX]; //最长公共子序列，动态规划求法
int maxLen(string s1, string s2){
    int length1 = s1.size();
    int length2 = s2.size();
    for (int i = 0; i < length1; ++i)
        MaxLen[i][0] = 0;
    for (int i = 0; i < length2; ++i)
        MaxLen[0][i] = 0;
     
    for (int i = 1; i <= length1; ++i)
    {
        for (int j = 1; j <= length2; ++j)
        {
            if (s1[i-1] == s2[j-1]){
                MaxLen[i][j] = MaxLen[i-1][j - 1] + 1;
            }
            else
            {
                MaxLen[i][j] = max(MaxLen[i - 1][j], MaxLen[i][j - 1]);
            }
        }
    }
 
    return MaxLen[length1][length2];
}
 
int main(){
    string s;
    while (cin >> s){
        int length = s.size();
        if (length == 1){
            cout << 1 << endl;
            continue;
        }
        //利用回文串的特点
        string s2 = s;
        reverse(s2.begin(),s2.end());
        int max_length = maxLen(s, s2);
        cout << length - max_length << endl;
    }
    return 0;
}