算法:动态规划基础
算法:动态规划基础
搞清动态规划与分治算法
分治法
为了解决一个给定的问题,算法需要一次或多次地递归调用其自身来解决相关的子问题。这些算法通常采用分治策略:将原问题划分为n个规模较小而结构与原问题相似的子问题;递归地解决这些子问题,然后再合并其结果,就得到原问题的解。
分治算法在每一层递归上都有是三个步骤:
- 分解:将原问题分解成一系列子问题。
- 解决:递归地解决子问题。若子问题足够小,则直接解决。
- 合并:将子问题的结果合并成原问题的解。
动态规划
动态规划适用于各子问题包含公共的子子问题。在这种情况下,若用分治法将会重复地求解公共的子子问题。动态规划算法对每个子子问题之求解一次,将其结果保存在一张表中,从而避免每次遇到各个子问题时重新计算答案。
动态规划算法的设计可分为四个步骤:
- 描述最优解结构。
- 递归定义最优解的值。
- 按自底向上的方法计算最优解的值。
- 由计算出来的结果构造一个最优解。
一道典型的DP题目
import java.util.Arrays;
public class Solution {
public int JumpFloorII(int target) {
if(target <= 2)
return target;
int[] dp = new int[target];
Arrays.fill(dp,1);
dp[0]=1;
for(int i=1;i<target;i++){
for(int j=0;j<i;j++)
dp[i]+=dp[j];
}
return dp[target-1];
}
}
解决思路
动态规划方法的最优化问题中的两个要素:最优子结构和重叠子问题。
描述最优解的结构
在寻找最优子结构时,可以遵循一种共同的模式:
- 问题的一个解可以做一个选择。做这种选择会得到一个或多个有待解决的子问题。
- 假设对一个给定的问题,已知的是一个可以导致最优解的选择。不必关心如何确定这个选择,尽管假设它是已知的。
- 在已知这个选择后,要确定哪些子问题会随之发生,以及如何最好地描述所得的子问题空间。
- 利用剪贴技术,来证明在问题的一个最优解中,使用的子问题的解本身也必须是最优的。
为了描述子问题空间,可以遵循这样一条有效的经验规则:就是尽量保证这个空间简单,然后在需要时再扩充它。
动态规划算法的运行时间依赖于两个因素:子问题的总个数和每个子问题中有多少个选择。
动态规划以自底向上的方式来利用最优子结构。也就是说,首要要找到子问题的最优解,解决子问题,然后找到问题的一个最优解。寻找问题的一个最优解需要在子问题中做出选择,即选择将用哪一个来求解问题。问题解的代价往往是子问题的代价加上选择本身带来的开销。
重叠子问题
适用于动态规划求解的最优化问题必须具备的第二个要素是子问题的空间要“很小”,也就是用来解决原问题的递归算法可反复解同样的子问题,而不是总在产生新的子问题。典型地,不同的子问题数是输入规模的一个多项式。当一个递归算法不断地调用同一个问题时,我们说该优化问题包含重叠子问题。相反的,适合用分治法解决的问题往往在递归的每一步都产生全新问题。
动态规划总是充分利用重叠子问题,即通过每个子问题只解一次,把解保存在一个在需要时就可以查看的表中,而每次查表的时间为常数。
做备忘录
动态规划有一种变形,它即具有通常的动态规划方法的效率,又采用了一种自顶向下的策略。其思想就是备忘原问题的自然但低效的递归算法。像在通常的动态规划中一样,维护一个记录了子问题的表,但有关填表动作的控制结构更像是递归算法。
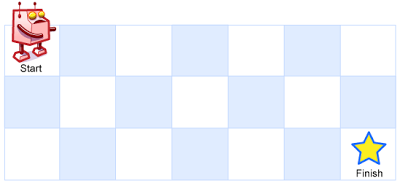
独特的路径
问题描述
机器人位于一个m x n网格的左上角(在下图中标记为“开始”)。 机器人只能随时向下或向右移动。机器人正在尝试到达网格的右下角(在下图中标记为“完成”)。 有多少可能的独特路径?
Java实现代码
class Solution {
public int uniquePaths(int n, int m) {
if(n==1)
return 1;
if(m==1)
return 1;
int[][] dp = new int[n][m];
dp[0][1] =1;
dp[1][0] =1;
for(int i = 0;i<n;i++) //i 是行
{
for(int j=0;j<m;j++) // j 是列
{
if((j==0&&i==1)||(i==0&&j==1)||(i==0&&j==0))
continue;
if(i==0)
dp[i][j]=dp[i][j-1];
else if(j==0)
dp[i][j]=dp[i-1][j];
else
dp[i][j] = dp[i-1][j]+dp[i][j-1];
}
}
return dp[n-1][m-1];
}
}
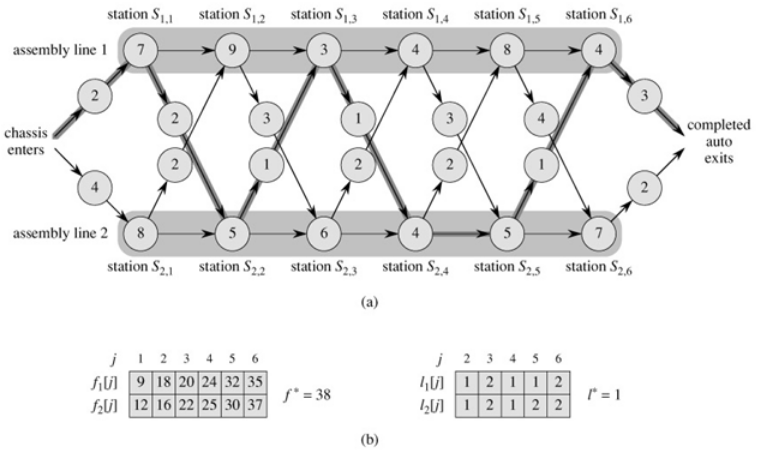
装配线问题
问题描述
有两条流水线,每条流水线都有n个站,流水线1,2站j的处理功能相同,但处理时间可能不同,每个站都有一个处理时间,而且从一条流水线的站j-1到另一条流水线站j有一个消耗时间t1[j-1](从流水线1到2)或t2[j-1](从流水线2到1),同一条流水线站j-1到站j的消耗时间忽略不计,物品上每一条流水线有个时间,下每一条流水线也有一个时间。问最快完成一个产品所需要的时间是多少?
Java实现代码
public void testDP() throws Exception {
int[][] a={{7,9,3,4,8,4},{8,5,6,4,5,7}};
int[][] t={{2,3,1,3,4},{2,1,2,2,1}};
int[][] f= {{0,0,0,0,0,0},{0,0,0,0,0,0}};
int[][] l= {{0,0,0,0,0,0},{0,0,0,0,0,0}};
int l_ =0;
f[0][0] =a[0][0]+2;
f[1][0]= a[1][0]+4;
for(int j=1;j<=5;j++)
{
//f[1][j]
if(f[0][j-1]+a[0][j]<=f[1][j-1]+a[0][j]+t[1][j-1])
{
f[0][j] = f[0][j-1]+a[0][j];
l[0][j]=1;
}else
{
f[0][j] = f[1][j-1]+a[0][j]+t[1][j-1];
l[0][j]=2;
}
//f[2][j]
if(f[1][j-1]+a[1][j]<=f[0][j-1]+a[1][j]+t[0][j-1])
{
f[1][j] = f[1][j-1]+a[1][j];
l[1][j]=2;
}else
{
f[1][j] = f[0][j-1]+a[1][j]+t[0][j-1];
l[1][j]=1;
}
}
if(f[0][5]<=f[1][5])
l_= 1;
else
l_ =2;
System.out.println("line"+l_+" station:"+6);
for(int i = 5;i>=1;i--)
{
l_ = l[l_-1][i];
System.out.println("line"+l_+" station:"+i);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号