数据结构：散列表

散列表

什么是哈西表：
　　一种具有相同特性的数据元素的集合，每个元素具有唯一标识自己的关键字。
基本原理：
　　说明：
　　　　顺序查找、二分查找或者二叉树的查找是基于待查关键字与表中元素的关键字进行比较而实现的查找方法。
　　　　散列查找是通过计算哈希函数来得到待查关键字的地址，理论上在哈希表中查找元素无需进行关键字间的比较。
　　　　计算哈希函数给出地址，从而找到元素K.
　　
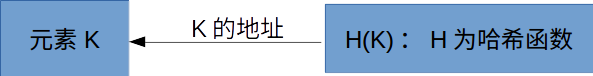
　　 例如：
　　　　假设有一个关键字序列18,75,60,43,54,90,46，给定哈希函数H(k)=k % 13，存贮区的内存地址从0到15，则可以得到每个关键字的散列地址：
　　　　　　H(18) = 18%13 = 5 H(75) = 75%13 = 10
　　　　　　H(60) = 60%13 = 8 H(43) = 43%13 = 4
　　　　　　H(54) = 54%13 = 2 H(90) = 90%13 = 12
　　　　根据散列地址，将7个关键字序列存储到一个一维数组(哈希表)中：
　　　　H(46) = 46%13 = 7
　　
　　 小结：
　　　　存储记录时，通过散列函数计算出记录的存储位置并按此存储位置存储记录：记录位置＝ Hash(记录的关键字)
　　　　访问记录时，利用散列函数计算存储位置，然后根据存储位置访问记录。

散列函数的构造方法

　　1.直接定址法：
　　　　H(key)=a*key+b a 和 b均为常数
　　2.数字分析法：
　　　　分析关键字的各个位的构成，截取其中若干位作为散列函数值，尽可能使关键字具有大的敏感度。
　　　　
　　3.平方取中法：
　　　　这种方法是先求关键字的平方值，然后在平方值中取中间几位为散列函数的值。因为一个数平方后的中间几位和原数的每一位都相关，因此，使用随机分布的关键字得到的记录的存储位置也是随机的。
　　4.折叠法：
　　　　将关键字分割成位数相同的几部分(最后一部分的位数可以不同)，然后取这几部分的叠加和(舍去进位)作为散列函数的值，称为折叠法。
　　　　例如，假设关键字为某人身份证号码430104681015355，则可以用4位为一组进行叠加，即有5355＋8101＋1046＋430＝14932，舍去高位，则有H(430104681015355)＝4932。
　　5.除留余数法：
　　　　Hash(key) = key % p
　　　　其中，p为不大于散列表表长m的整数

解决冲突的方法

1.开放地址法：

　　☐开放定址法就是从发生冲突的那个单元开始，按照一定的次序，从哈希表中找出一个空闲的存储单元，把发生冲突的待插入关键字存储到该单元中，从而解决冲突。在哈希表未填满时，处理冲突需要的“下一个”空地址在哈希表中解决。
　　☐公式：Hi = (H(key)+di) MOD m i=1,2,…K(K<=m-1) di为增量序列、m为散列表长度。
　　☐根据di的取值，细分为：
　　☐ 线性探测再散列
　　　　☐
　　　　☐ 若一个关键字在地址d处发生冲突，则依次探查d+1，d+2，…，达到表尾时，又从0，1，2，….开始探查，直到找到一个空闲位置来存储冲突的关键字。
　　　　☐ d1= 1 d2= 2 d3= 3 … dm-1= m-1
　　☐ 二次探测再散列
　　　　☐ 假设哈希表的地址为0~m-1，则哈希表的长度为m。若一个关键字在地址d处发生冲突，则依次探查位置d+1²，d-1², d+2², d-2², …, 直到找到一个空闲位置为止。
　　　　☐ Hi = (H(key)+di) MOD m i = 1,2,…,k (k≤m-1)
　　　　☐ d1= 1² d2= -1² d3= 2² d4= -2² …

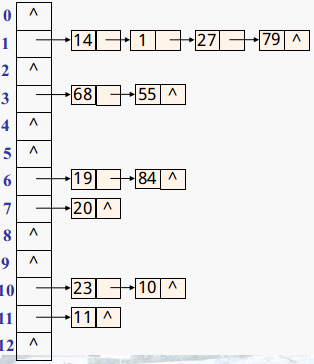
2.链地址法

　　☐链地址法也称为拉链法，是将所有关键字为同义词的记录存储在同一个线性链表中。
　　☐ 实例：
　　　　☐ 例如: 给定关键字序列如下，散列函数为H(k)=k%13 。19，14，23，1，68，20，84，27，55，11，10，79 试用链地址法建立散列表。
　　　　☐ 计算散列值:
　　　　☐
　　　　☐