数据结构：顺序栈的实现

数据结构：顺序栈的实现

1、快速开始

　　栈是一种遵循元素后进(Push)先出(Pop)规则的线性表，即最后加入的元素最先出来，它的实现可以用数组或者链表。

　　

　　

　　它的特点如下：

• 后入先出，先入后出。
• 除了头尾节点之外，每一个元素有一个前驱，有一个后继。　　

 

2、实现栈

　　我们已经说过了，栈是一种线性表，故其底层是基于数组或者链表的。那么，我们的重点是维护一种规则，即后进先出。

　　我们始终要有一个变量L来记录最后一个元素的位置：

• 当压入时，将新元素插入到L位置之后，然后更新L，即L+1.
  • 
• 当弹出时，将L位置元素进行删除，然后更新L，即L-1。
  • 

     

 　　也正是因为，我们使用的是线性表，正好可以利用其尺寸来表示L，即线性表的大小可以表示最后一个元素的位置。

2.1、栈的实现 

class MyStack {
    private List<Integer> data;               // 存储元素
    public MyStack() {
        data = new ArrayList<>();
    }
    /**插入一个元素到栈中. */
    public void push(int x) {
        data.add(x);
    }
    /**检查是否为空 */
    public boolean isEmpty() {
        return data.isEmpty();
    }
    /**到达栈顶. */
    public int top() {
        return data.get(data.size() - 1);
    }
    /** 删除一个元素. 操作成功返回true. */
    public boolean pop() {
        if (isEmpty()) {
            return false;
        }
        data.remove(data.size() - 1);
        return true;
    }
};

　　

3、C语言版本实现

3.1、对栈的结构定义：

typedef struct
{
   int *base; 
   int *top; 
   int stacksize;    
}SqStack;

说明：

　　　　1.base表示栈底指针，在判断出栈、初始化和重新分配空间的时候需要用到。

　　　　2.top表示栈顶指针，是栈最关键和核心的组成，入栈时top向上移动，出栈时top向下移动。

　　　　3.此处的stacksize并不表示当前的栈中的元素数量，而是表示栈的容量，也就是能装多少个元素。

3.2、初始化栈：

int initStack(SqSatck *S)
{
    S->base=(int*)malloc(100*sizeof(int));
    if(!S)
         return 0; //0代表操作失败
    S->top=S->base;
    stacksize=100;
    return 1; //1代表操作完成
}

说明：

　　　　1.顺序栈初始化无非就是给栈分配连续的内存空间，base是栈底指针，在上面提到过，它用来指示一段连续的内存空间的首地址，也就是用来初始化。

　　　　2.分配空间不意味着一定会有那么多空间，所以判断也不可缺少。

　　　　3.分配空间后，base和top的地址应该一致，此时top还没有移动。

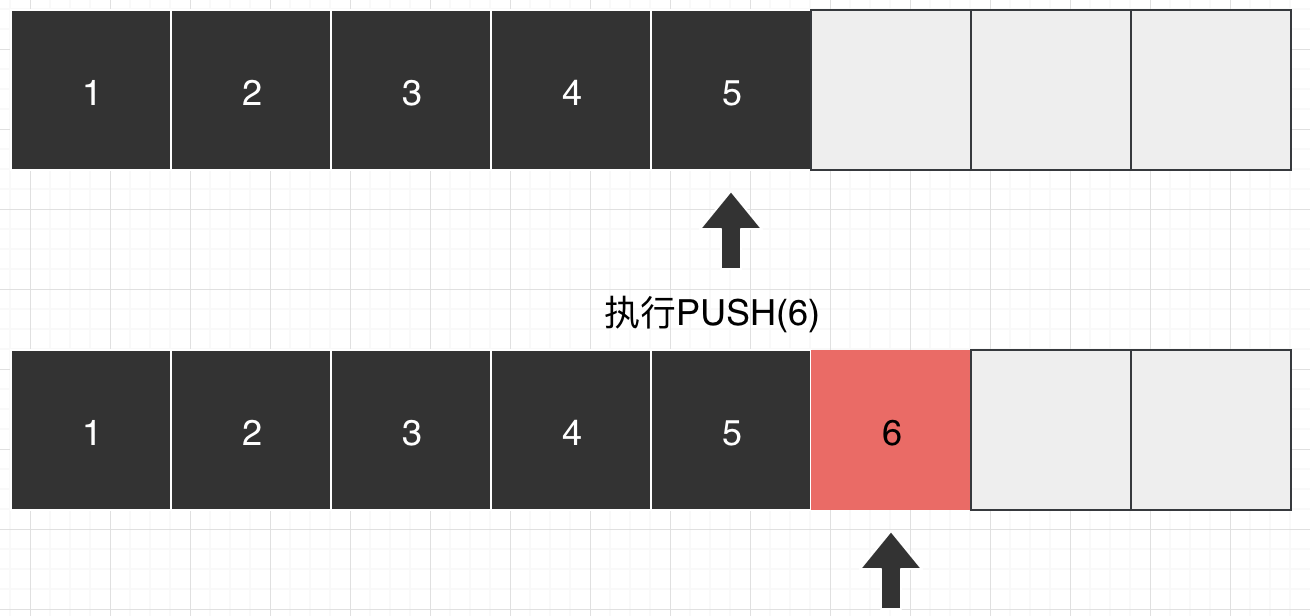
3.3、压栈

int push(SqStack * S,int elem)
{
  if(S->top-S->base>=S->stacksize)
  {
        S->base=(SElemType *)
                realloc(S->base,(S->stacksize+10)*sizeof(SElemType)); //10代表增量，你可以使用宏定义，方便后续修改。
        if(!S->base)
            return 0;
        S->top=S->base+S->stacksize;
        S->stacksize+=10
  }
  *S->top++=elem;
  return 1;
}    

　　说明：

　　　　1.压栈是栈的核心操作，关键步骤无非是*S->top++=elem;但是在进行此步操作时，一定要判断栈是否超出容量。

　　　　2.如果栈超出容量，则要在进行原空间的基础上重新分配空间，realloc是关键的命令。

　　realloc 
　　　　原型：extern void *realloc(void *mem_address, unsigned int newsize); 
　　　　用法：#include <stdlib.h> 有些编译器需要#include <alloc.h> 
　　　　功能：改变mem_address所指内存区域的大小为newsize长度。 
　　　　说明：如果重新分配成功则返回指向被分配内存的指针，否则返回空指针NULL。 
　　　　当内存不再使用时，应使用free()函数将内存块释放。 

　　　　3.分配空间以后，在修改stacksize之前，top应该保持在容量顶端，S->top=S->base+S->stacksize;

2.4出栈

int pop(SqStack *q)
{
    if(S->top==S->base)
          return 0;
    return *S->--top;;
}

说明：

　　　　1.出栈是简单操作，其实这里并没有完美的实现这个效果，你应该考虑到如果在扩容后又迅速减小，会造成大量的空间浪费。 

2.5遍历栈

int printfStack(SqStack *S)
{
    int *p=S->base;
    puts("输出栈");
    for(p;p!=S->top;p++)
    {
        printf("***%d",*p);
    }
}