CNN学习笔记：激活函数

CNN学习笔记：激活函数

激活函数

　　激活函数又称非线性映射，顾名思义，激活函数的引入是为了增加整个网络的表达能力（即非线性）。若干线性操作层的堆叠仍然只能起到线性映射的作用，无法形成复杂的函数。常用的函数有sigmoid、双曲正切、线性修正单元函数等等。 使用一个神经网络时，需要决定使用哪种激活函数用隐藏层上，哪种用在输出节点上。 

　　比如，在神经网路的前向传播中，这两步会使用到sigmoid函数。sigmoid函数在这里被称为激活函数。

sigmoid函数

　　之前在线性回归中，我们用过这个函数，使我们的输出值平滑地处于0~1之间。

　　

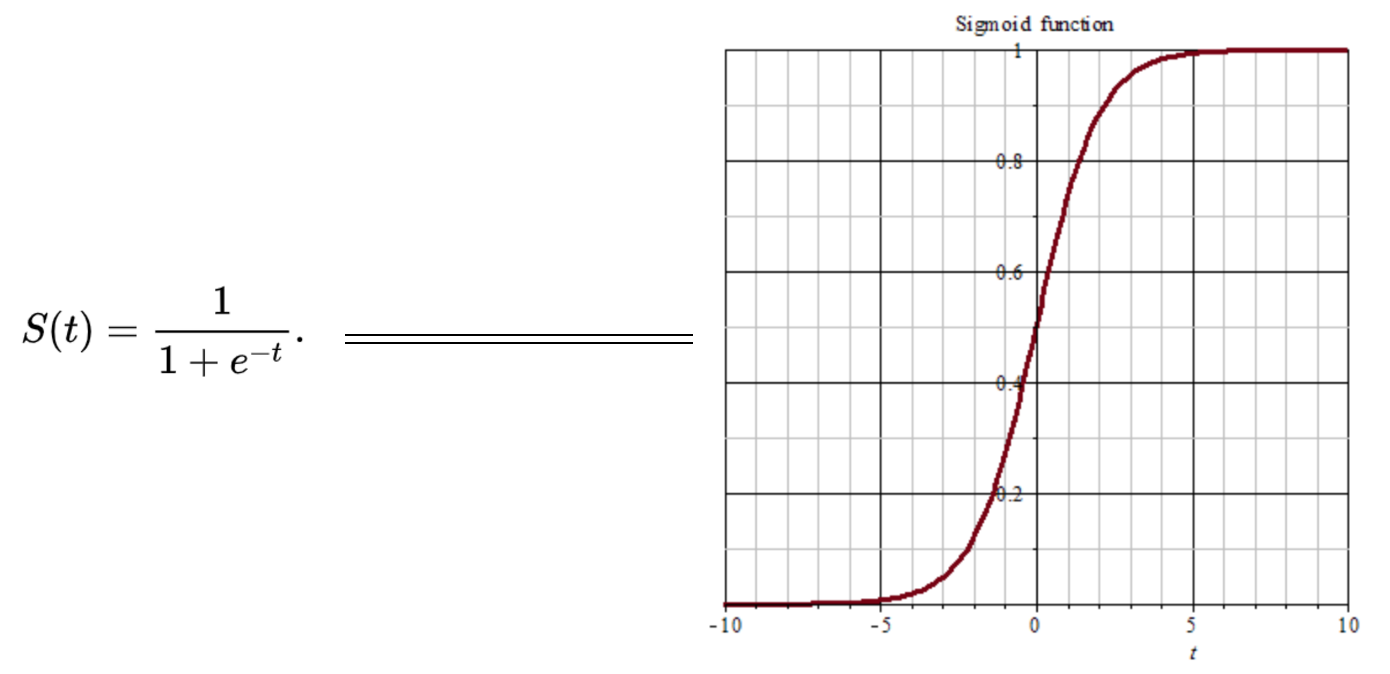
　　观察图形我们发现，当大于5或者小于-5的值无论多大或多小都会被压缩到1或0。如此便带来一个严重问题，即梯度的“饱和效应”。大于5或者小于-5部分的梯度接近0，这回导致在误差反向传播过程中导数处于该区域的误差就很难甚至根本无法传递至前层，进而导致整个网络无法训练（导数为0将无法跟新网络参数）。

　　此外，在参数初始化的时候还需要特别注意，要避免初始化参数直接将输出值带入这一区域，比如初始化参数过大，将直接引发梯度饱和效应而无法训练。

说明：除非输出层是一个二分类问题否则基本不会用它。

双曲正切函数

　　tanh函数是sigmoid的向下平移和伸缩后的结果。对它进行了变形后，穿过了原点，并且值域介于+1和-1之间。

　　

　　结果表明，如果在隐藏层上使用函数tanh效果总是优于sigmoid函数。因为函数值域在-1和+1的激活函数，其均值是更接近零均值的。在训练一个算法模型时，如果使用tanh函数代替sigmoid函数中心化数据，使得数据的平均值更接近0而不是0.5.

说明：tanh是非常优秀的，几乎适合所有场合

修正线性单元的函数（ReLu）

　　sigmoid函数与双曲正切函数都有一个共同的问题，在Z特别大或者特别小的情况下，导致梯度或者函数的斜率变得特别小，最后就会接近于0，导致降低梯度下降的速度。

　　线性整流函数（Rectified Linear Unit, ReLU）,又称修正线性单元, 是一种人工神经网络中常用的激活函数（activation function），通常指代以斜坡函数及其变种为代表的非线性函数。

　　

　　

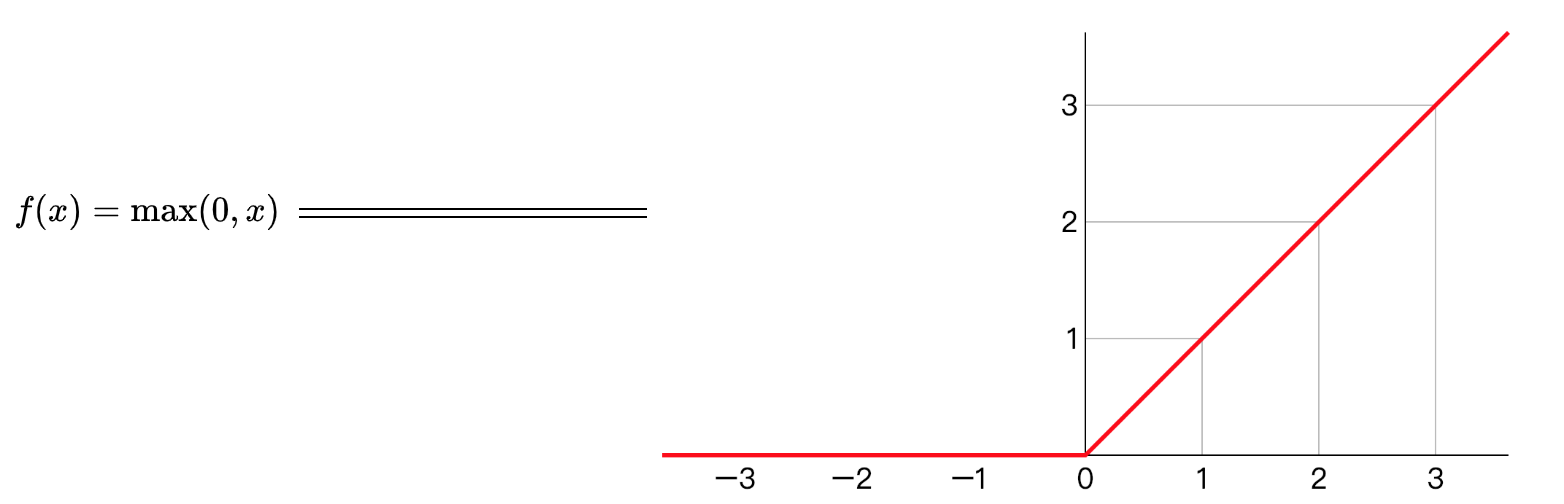
　　Relu作为神经元的激活函数，定义了该神经元在线性变换 之后的非线性输出结果。换言之，对于进入神经元的来自上一层神经网络的输入向量，使用线性整流激活函数的神经元会输出至下一层神经元或作为整个神经网络的输出（取决现神经元在网络结构中所处位置）。

　　只要是W^TX+b正值的情况下，导数恒等于1，当W^TX+b是负值的时候，导数恒等于0。从实际上来说，当使用的导数时，W^TX+b=0的导数是没有定义的。

选择激活函数的经验法则：

　　如果输出是0、1值（二分类问题），则输出层选择sigmoid函数，然后其它的所有单元都选择Relu函数。

　　最常用的默认函数，，如果不确定用哪个激活函数，就使用ReLu或者Leaky ReLu

带泄露线性整流函数（Leaky ReLU）

　　在输入值 为负的时候，带泄露线性整流函数（Leaky ReLU）的梯度为一个常数 ，而不是0。在输入值为正的时候，带泄露线性整流函数和普通斜坡函数保持一致。

　　

　　在深度学习中，如果设定  为一个可通过反向传播算法（Backpropagation）学习的变量，那么带泄露线性整流又被称为参数线性整流（Parametric ReLU）