CNN学习笔记：线性回归

CNN学习笔记：Logistic回归

线性回归

二分类问题

　　Logistic回归是一个用于二分分类的算法，比如我们有一张图片，判断其是否为一张猫图，为猫输出1，否则输出0。

　　

基本术语

　　进行机器学习，首先要有数据，比如我们收集了一批关于西瓜的数据，例如

　　（色泽=青绿；根蒂=收缩；敲声=浊响）

　　（色泽=乌黑；根蒂=稍蜷；敲声=沉闷）

　　（色泽=浅白；根蒂=硬挺；敲声=清脆）

　　每对括号内是一条记录，这组记录的集合称为一个数据集，每条记录是关于一个事件或对象的描述，称为一个示例或样本，反映事件或对象在某方面的表现或性质的事项。例如“色泽’、“根蒂”、"敲声”,称为“属性”(attribute) 或“特征”(feature); 属性上的取值,例如“青绿”“乌黑”，称为“属性值”(attribute value).属性张成的空间称为“属性空间”(attribute space)、“ 样本空间”(sample space)或“输入空间”.例如我们把“色泽”“根蒂”“敲声”作为三个坐标轴，则它们张成一个用于描述西瓜的三维空间，每个西瓜都可在这个空间中找到自己的坐标位置.由于空间中的每个点对应一个坐标向量,因此我们也把一个示例称为-一个“特征向量”(feature vector)。

关于线性回归

　　给定数据集D={(x1, y1), (x2, y2), ... }，我们试图从此数据集中学习得到一个线性模型，这个模型尽可能准确地反应x(i)和y(i)的对应关系。这里的线性模型，就是属性(x)的线性组合的函数，可表示为：

　　

　　向量表示为

　　

　　其中

　　

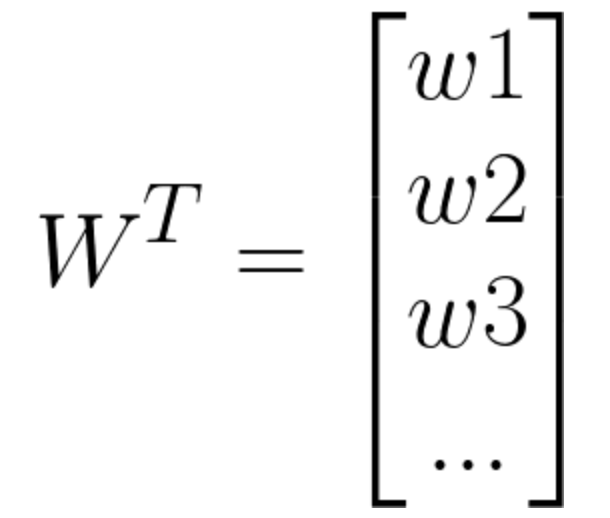
　　W在这里称为权重，直观的表达了各属性在预测中的重要性，因此线性模型有很好的可解释性，例如西瓜问题中学到如下图的模型，那么意味着通过考虑色泽、根蒂和敲声来判断挂的好坏，其中根蒂最重要，敲声次之。

　　

　　线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记：

　　

　　这称为多元线性回归。

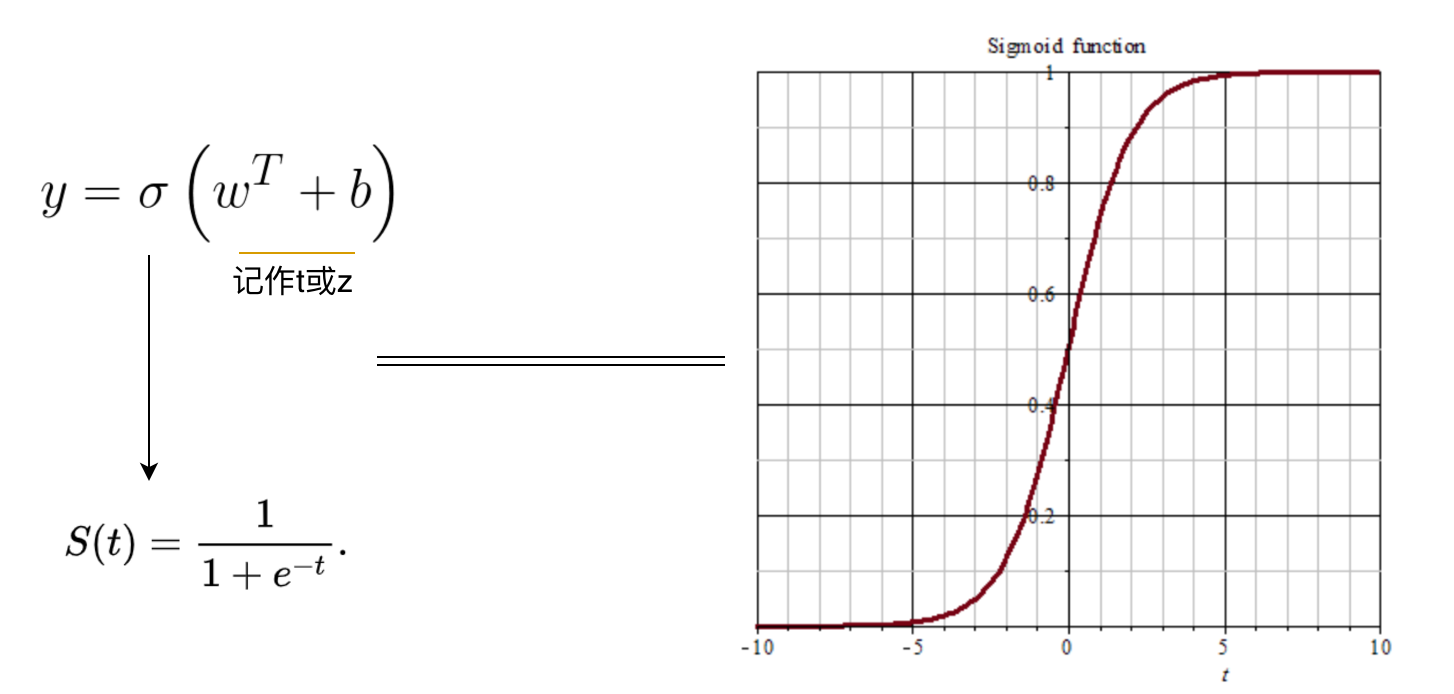
S函数

　　我们在做概率估计的时候，预测值处于0~1之间，Sigmod函数正是这样一条平滑曲线，我们可以借助它来预测概率。

　　

损失函数

　　如何确定w和b，关键在于衡量f(x)与y之间的差异。均方误差是回归任务中最常用的性能度量，因此我们可试图让均方误差最小化，即：

　　

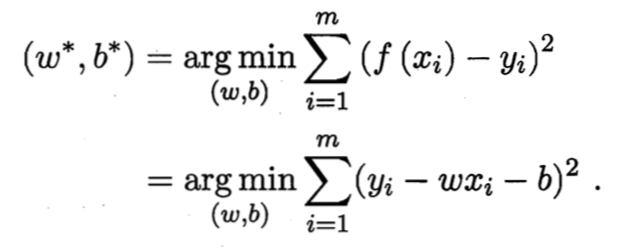
　　均方误差有非常好的集合意义，他对应了常用的欧几里得距离或欧式距离。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归中，最小二乘法就是试图找到一条直线，是所有样本到直线上的欧式距离之和最小。

Keras实践——线性回归

import keras
import numpy as np
import matplotlib.pyplot as plt
 #顺序模型
from keras.models import  Sequential
 #全连接层
from keras.layers import Dense

#使用numpy生成100个随机点
x_data = np.random.rand(100)
noise = np.random.normal(0,0.01,x_data.shape)
y_data = x_data * 0.1 +0.2 +noise

#显示随机点
plt.scatter(x_data,y_data)
plt.show()


#构建一个顺序模型
model = Sequential()
#在模型中添加一个全连接层
model.add(Dense(units=1,input_dim=1))
model.compile(optimizer='sgd',loss='mse')

for step in range(3001):
    #每次训练一个批次
    cost = model.train_on_batch(x_data,y_data)
    #每500次打印一下cost值
    if step %500 ==0:
        print("COST",cost)

#打印权值和偏执值
w,b = model.layers[0].get_weights()
print("权值",w,"偏执值",b)

# x_data输入网络中，得到预测值
y_pred = model.predict(x_data)

#显示随机点
plt.scatter(x_data,y_data)
plt.plot(x_data,y_pred,'r-',3)
plt.show()

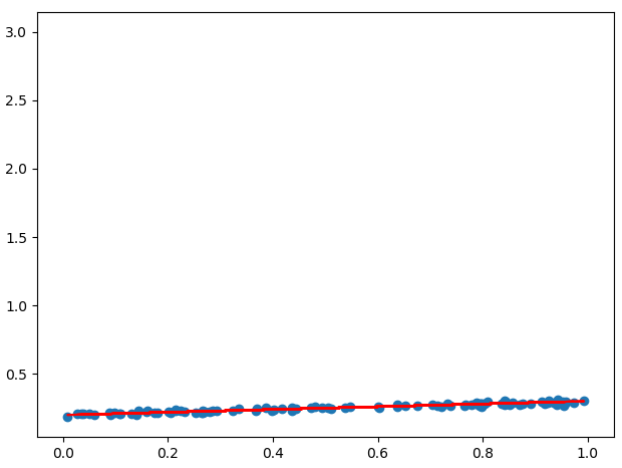
　　拟合效果如下：