链表问题集锦
链表节点的结构:
struct ListNode {
int val;
ListNode* next;
ListNode(int _val = -1)
{
val = _val;
next = nullptr;
}
};
一、在O(1)时间删除链表节点
题目描述:给定链表的头指针和一个节点指针,在O(1)时间删除该节点。[Google面试题]
分析:本题与《编程之美》上的「从无头单链表中删除节点」类似。主要思想都是「狸猫换太子」,即用下一个节点数据覆盖要删除的节点,然后删除下一个节点。但是如果节点是尾节点时,该方法就行不通了。
代码:如下
1 void DeleteRandomNode(ListNode* cur)
2 {
3 assert(cur == nullptr); //不能是空节点
4 assert(cur->next == nullptr); //不能是尾节点
5 ListNode* pnext = cur->next;
6 cur->val = pnext->val;
7 cur->next = pnext->next;
8 }
二、求链表倒数第k个节点
题目描述:输入一个单向链表,输出该链表中倒数第k个节点,链表的倒数第0个节点为链表的尾指针。
分析:设置两个指针 p1、p2,首先 p1 和 p2 都指向 head,然后 p2 向前走 k 步,这样 p1 和 p2 之间就间隔 k 个节点,最后 p1 和 p2 同时向前移动,直至 p2 走到链表末尾。
代码:如下
1 ListNode* TheKthListNode(ListNode* head, int k)
2 {
3 ListNode* node = head;
4 while (k)
5 {
6 node = node->next;
7 k--;
8 }
9 while (node)
10 {
11 node = node->next;
12 head = head->next;
13 }
14 return head;
15 }
三、求链表中间节点
题目描述:求链表的中间节点,如果链表的长度为偶数,返回中间两个节点的任意一个,若为奇数,则返回中间节点。
分析:此题的解决思路和第3题「求链表的倒数第 k 个节点」很相似。可以先求链表的长度,然后计算出中间节点所在链表顺序的位置。但是如果要求只能扫描一遍链表,如何解决呢?最高效的解法和第3题一样,通过两个指针来完成。用两个指针从链表头节点开始,一个指针每次向后移动两步,一个每次移动一步,直到快指针移到到尾节点,那么慢指针即是所求。
代码:如下
1 ListNode* TheMidListNode(ListNode* head)
2 {
3 ListNode* slow = head;
4 ListNode* fast = head;
5
6 while (fast && fast->next)
7 {
8 slow = slow->next;
9 fast = fast->next->next;
10 }
11
12 return slow;
13 }
四、判断单链表是否存在环
题目描述:输入一个单向链表,判断链表是否有环?
分析:通过两个指针,分别从链表的头节点出发,一个每次向后移动一步,另一个移动两步,两个指针移动速度不一样,如果存在环,那么两个指针一定会在环里相遇。
代码:如下
1 bool HasCircle(ListNode* &head)
2 {
3 if (head == nullptr || head->next == nullptr)
4 return false;
5
6 ListNode* slow = head;
7 ListNode* fast = head;
8
9 while (fast && fast->next)
10 {
11 fast = fast->next->next;
12 slow = slow->next;
13 if (slow == fast)
14 return true;
15 }
16 return false;
17 }
五、找到环的入口点
题目描述:输入一个单向链表,判断链表是否有环。如果链表存在环,如何找到环的入口点?
分析:由上题可知,按照 p2 每次两步,p1 每次一步的方式走,发现 p2 和 p1 重合,确定了单向链表有环路了。接下来,让p2回到链表的头部,重新走,每次步长不是走2了,而是走1,那么当 p1 和 p2 再次相遇的时候,就是环路的入口了。
为什么:假定起点到环入口点的距离为 a,p1 和 p2 的相交点M与环入口点的距离为b,环路的周长为L,当 p1 和 p2 第一次相遇的时候,假定 p1 走了 n 步。那么有:p1走的路径: a+b = n;p2走的路径: a+b+k*L = 2*n; p2 比 p1 多走了k圈环路,总路程是p1的2倍
根据上述公式可以得到 k*L=a+b=n显然,如果从相遇点M开始,p1 再走 n 步的话,还可以再回到相遇点,同时p2从头开始走的话,经过n步,也会达到相遇点M。
显然在这个步骤当中 p1 和 p2 只有前 a 步走的路径不同,所以当 p1 和 p2 再次重合的时候,必然是在链表的环路入口点上。
代码:如下
1 ListNode* FindLoopPort(ListNode* head)
2 {
3 if (head == nullptr || head->next == nullptr)
4 return nullptr;
5
6 ListNode* slow = head;
7 ListNode* fast = head;
8
9 while (fast && fast->next)
10 {
11 fast = fast->next->next;
12 slow = slow->next;
13 if (slow == fast)
14 break;
15 }
16
17 if (slow != fast)
18 return nullptr;
19
20 fast = head;
21
22 while (fast != slow)
23 {
24 fast = fast->next;
25 slow = slow->next;
26 }
27
28 return slow;
29 }
六、判断两个链表是否相交
题目描述:给出两个单向链表的头指针(如下图所示),判断这两个链表是否相交。这里为了简化问题,我们假设两个链表均不带环。
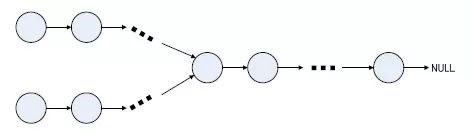
分析:
1、直接循环判断第一个链表的每个节点是否在第二个链表中。但,这种方法的时间复杂度为O(Length(h1) * Length(h2))。显然,我们得找到一种更为有效的方法,至少不能是O(N^2)的复杂度。
2、针对第一个链表直接构造hash表,然后查询hash表,判断第二个链表的每个节点是否在hash表出现,如果所有的第二个链表的节点都能在hash表中找到,即说明第二个链表与第一个链表有相同的节点。时间复杂度为为线性:O(Length(h1) + Length(h2)),同时为了存储第一个链表的所有节点,空间复杂度为O(Length(h1))。是否还有更好的方法呢,既能够以线性时间复杂度解决问题,又能减少存储空间?
3、转换为环的问题。把第二个链表接在第一个链表后面,如果得到的链表有环,则说明两个链表相交。如何判断有环的问题上面已经讨论过了,但这里有更简单的方法。因为如果有环,则第二个链表的表头一定也在环上,即第二个链表会构成一个循环链表,我们只需要遍历第二个链表,看是否会回到起始点就可以判断出来。这个方法的时间复杂度是线性的,空间是常熟。
4、进一步考虑“如果两个没有环的链表相交于某一节点,那么在这个节点之后的所有节点都是两个链表共有的”这个特点,我们可以知道,如果它们相交,则最后一个节点一定是共有的。而我们很容易能得到链表的最后一个节点,所以这成了我们简化解法的一个主要突破口。那么,我们只要判断两个链表的尾指针是否相等。相等,则链表相交;否则,链表不相交。
所以,先遍历第一个链表,记住最后一个节点。然后遍历第二个链表,到最后一个节点时和第一个链表的最后一个节点做比较,如果相同,则相交,否则,不相交。这样我们就得到了一个时间复杂度,它为O((Length(h1) + Length(h2)),而且只用了一个额外的指针来存储最后一个节点。这个方法时间复杂度为线性O(N),空间复杂度为O(1),显然比解法三更胜一筹。
代码:如下
1 ListNode* IsIntersect(ListNode* head1, ListNode* head2)
2 {
3 ListNode* node1 = head1;
4 ListNode* node2 = head2;
5
6 while (node1 != node2)
7 {
8 node1 = node1 == nullptr ? head2 : node1->next;
9 node2 = node2 == nullptr ? head1 : node2->next;
10 }
11
12 return node1;
13 }
七、两个链表相交的第一个公共节点
题目描述:如果两个无环单链表相交,怎么求出他们相交的第一个节点呢?
分析:采用对齐的思想。计算两个链表的长度 L1 , L2,分别用两个指针 p1 , p2 指向两个链表的头,然后将较长链表的 p1(假设为 p1)向后移动L2 - L1个节点,然后再同时向后移动p1 , p2,直到 p1 = p2。相遇的点就是相交的第一个节点。
代码:如下
1 ListNode* FindIntersectListNode(ListNode* head1, ListNode* head2)
2 {
3 ListNode* node1 = head1;
4 ListNode* node2 = head2;
5
6
7 int len1 = 0, len2 = 0;
8 while (node1)
9 {
10 node1 = node1->next;
11 len1++;
12 }
13 while (node2)
14 {
15 node2 = node2->next;
16 len2++;
17 }
18
19 node1 = head1;
20 node2 = head2;
21 if (len1 > len2)
22 {
23 while (len1 > len2)
24 {
25 node1 = node1->next;
26 len1--;
27 }
28 }
29 else
30 {
31 while (len2 > len1)
32 {
33 node2 = node2->next;
34 len2--;
35 }
36 }
37
38 while (node1 != node2)
39 {
40 node1 = node1->next;
41 node2 = node2->next;
42 }
43
44 return node1;
45 }
八、链表有环,如何判断相交
题目描述:上面的问题都是针对链表无环的,那么如果现在,链表是有环的呢?上面的方法还同样有效么?
分析:如果有环且两个链表相交,则两个链表都有共同一个环,即环上的任意一个节点都存在于两个链表上。因此,就可以判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
代码:如下
1 bool HasCircle(ListNode* head, ListNode* &node)
2 {
3 node = nullptr;
4 if (head == nullptr || head->next == nullptr)
5 return false;
6
7 ListNode* slow = head;
8 ListNode* fast = head;
9
10 while (fast && fast->next)
11 {
12 fast = fast->next->next;
13 slow = slow->next;
14 if (slow == fast)
15 {
16 node = slow;
17 return true;
18 }
19 }
20
21 return false;
22 }
23
24
25 bool IsIntersectWithLoop(ListNode* head1, ListNode* head2)
26 {
27 ListNode* CircleNode1 = nullptr, *CircleNode2 = nullptr;
28 if (!HasCircle(head1, CircleNode1))
29 return false;
30 if (!HasCircle(head2, CircleNode2))
31 return false;
32
33 ListNode* temp = CircleNode2->next;
34 while (temp != CircleNode2)
35 {
36 if (temp == CircleNode1)
37 return true;
38 temp = temp->next;
39 }
40 return false;
41 }
九、两个可能有环链表相交找交点
第一种情况:两个链表都有环且不相交
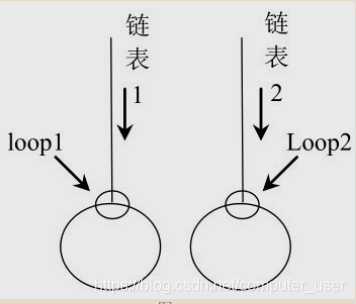
第二种情况:两个链表都有环且不相交两个链表都有环相交,交点不在环上,或正好在入口点
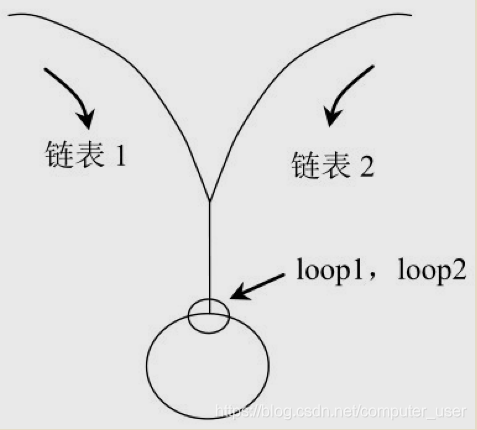
第三种情况:两个链表都有环且不相交两个链表都有环相交,交点在环上
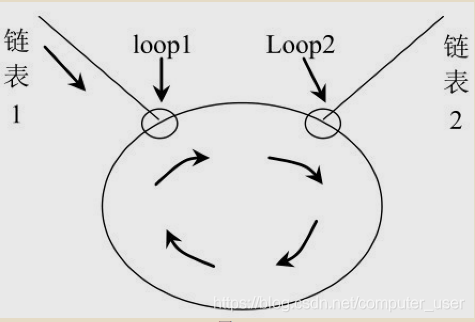
第二种情况和无环相交类似,只是快节点走到null改为快节点走到环入口点
第三种情况,第一种情况 --> 找到两个链表的入口点,让一个链表的节点继续走,如果走一圈又走回来了没有碰到另一个入口点说明为情况1,若遇到了说明为情况2。
解决:
1 ListNode* FindLoopPort(ListNode* head)
2 {
3 if (head == nullptr || head->next == nullptr)
4 return nullptr;
5
6 ListNode* slow = head;
7 ListNode* fast = head;
8
9 while (fast && fast->next)
10 {
11 fast = fast->next->next;
12 slow = slow->next;
13 if (slow == fast)
14 break;
15 }
16
17 if (slow != fast)
18 return nullptr;
19
20 fast = head;
21
22 while (fast != slow)
23 {
24 fast = fast->next;
25 slow = slow->next;
26 }
27
28 return slow;
29 }
30
31
32 ListNode* FindIntersectWithLoopListNode(ListNode* head1, ListNode* head2)
33 {
34 if (head1 == nullptr || head2 == nullptr)
35 return nullptr;
36
37 ListNode* loop1 = FindLoopPort(head1);
38 ListNode* loop2 = FindLoopPort(head2);
39
40
41 if (loop1 == nullptr || loop2 == nullptr) //必有一个无环
42 {
43 return nullptr;
44 }
45
46 if (loop1 == loop2)
47 {
48 int len1 = 0;
49 ListNode* node1 = head1;
50 while (node1)
51 {
52 len1++;
53 node1 = node1->next;
54 }
55
56 int len2 = 0;
57 ListNode* node2 = head2;
58 while (node2)
59 {
60 len2++;
61 node2 = node2->next;
62 }
63
64 node1 = head1;
65 node2 = head2;
66
67 if (len1 > len2)
68 {
69
70 while (len1 > len2)
71 {
72 node1 = node1->next;
73 len1--;
74 }
75 }
76 else
77 {
78 while (len2 > len1)
79 {
80 node2 = node2->next;
81 len2--;
82 }
83 }
84
85 while (node1 != node2)
86 {
87 node1 = node1->next;
88 node2 = node2->next;
89 }
90 }
91 else
92 {
93 ListNode* node = loop1->next;
94 while (node != loop1)
95 {
96 if (node == loop2)
97 return node;
98 node = node->next;
99 }
100 return nullptr;
101 }
102
103 return nullptr;
104 }
十、单链表的反转
题目描述:输入一个单向链表,输出逆序反转后的链表
分析:链表的转置是一个很常见、很基础的数据结构题了,非递归的算法很简单,用三个临时指针 pre、head、next 在链表上循环一遍即可。递归算法也是比较简单的,但是如果思路不清晰估计一时半会儿也写不出来吧。
代码:如下
1 ListNode* ReverseList(ListNode* head)
2 {
3 if (head == nullptr || head->next == nullptr)
4 return head;
5
6 ListNode* vhead = new ListNode(-1);
7
8 while (head)
9 {
10 ListNode* node = head->next;
11 head->next = vhead->next;
12 vhead->next = head;
13 head = node;
14 }
15 return vhead->next;
16 }
递归写法:
1 ListNode* ReverseList(ListNode* head)
2 {
3 if (head == nullptr || head->next == nullptr)
4 return head;
5
6 ListNode* node = head->next;
7 ListNode* newhead = ReverseList(head->next);
8
9 node->next = head;
10 head->next = nullptr;
11 return newhead;
12 }
十一、k个一组进行链表反转
k个节点为一组进行反转,不足k个的部分不需要反转。

1 #include <iostream> 2 #include <vector> 3 4 using namespace std; 5 6 struct ListNode { 7 int val; 8 ListNode* next; 9 ListNode(int _val) 10 { 11 val = _val; 12 next = nullptr; 13 } 14 }; 15 16 17 ListNode* CreateList(vector<int> reg) 18 { 19 ListNode* vhead = new ListNode(-1); 20 ListNode* tail = vhead; 21 22 for (int i = 0; i < reg.size(); i++) 23 { 24 ListNode* node = new ListNode(reg[i]); 25 tail->next = node; 26 tail = node; 27 } 28 return vhead->next; 29 } 30 31 void PrintList(ListNode* head) 32 { 33 while (head) 34 { 35 cout << head->val << " "; 36 head = head->next; 37 } 38 cout << endl; 39 } 40 41 ListNode* ReverseList(ListNode* head, int k) 42 { 43 if (head == nullptr || head->next == nullptr || k == 1) 44 return head; 45 46 int len = 0; 47 48 ListNode* node = head; 49 while (node) 50 { 51 len++; 52 node = node->next; 53 } 54 55 int cnt = len / k; 56 57 ListNode* vhead = new ListNode(-1); 58 ListNode* vtail = vhead; 59 node = head; 60 while (cnt) 61 { 62 int t = k; 63 ListNode* thead = new ListNode(-1); 64 ListNode* end = nullptr; 65 while (t) 66 { 67 if (end == nullptr) 68 end = node; 69 ListNode* temp = node->next; 70 node->next = thead->next; 71 thead->next = node; 72 node = temp; 73 t--; 74 } 75 vtail->next = thead->next; 76 vtail = end; 77 cnt--; 78 } 79 vtail->next = node; 80 return vhead->next; 81 } 82 83 int main() 84 { 85 vector<int> reg = { 1,2,3,4,5,6,7 }; 86 87 ListNode* head = CreateList(reg); 88 89 PrintList(head); 90 91 ListNode* newhead = ReverseList(head, 3); 92 93 PrintList(newhead); 94 return 0; 95 }
十二、指定区域链表反转
题目描述:给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例1:
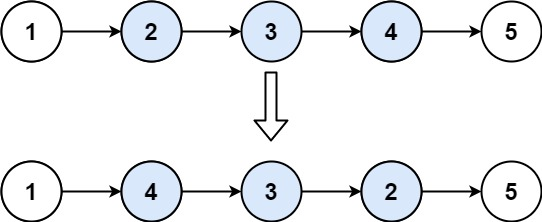
解法一:
整体思想是:在需要反转的区间里,每遍历到一个节点,让这个新节点来到反转部分的起始位置。下面的图展示了整个流程。

下面我们具体解释如何实现。使用三个指针变量 pre、curr、next 来记录反转的过程中需要的变量,它们的意义如下:
curr:指向待反转区域的第一个节点 left;
next:永远指向 curr 的下一个节点,循环过程中,curr 变化以后 next 会变化;
pre:永远指向待反转区域的第一个节点 left 的前一个节点,在循环过程中不变。
第 1 步,我们使用 ①、②、③ 标注「穿针引线」的步骤。
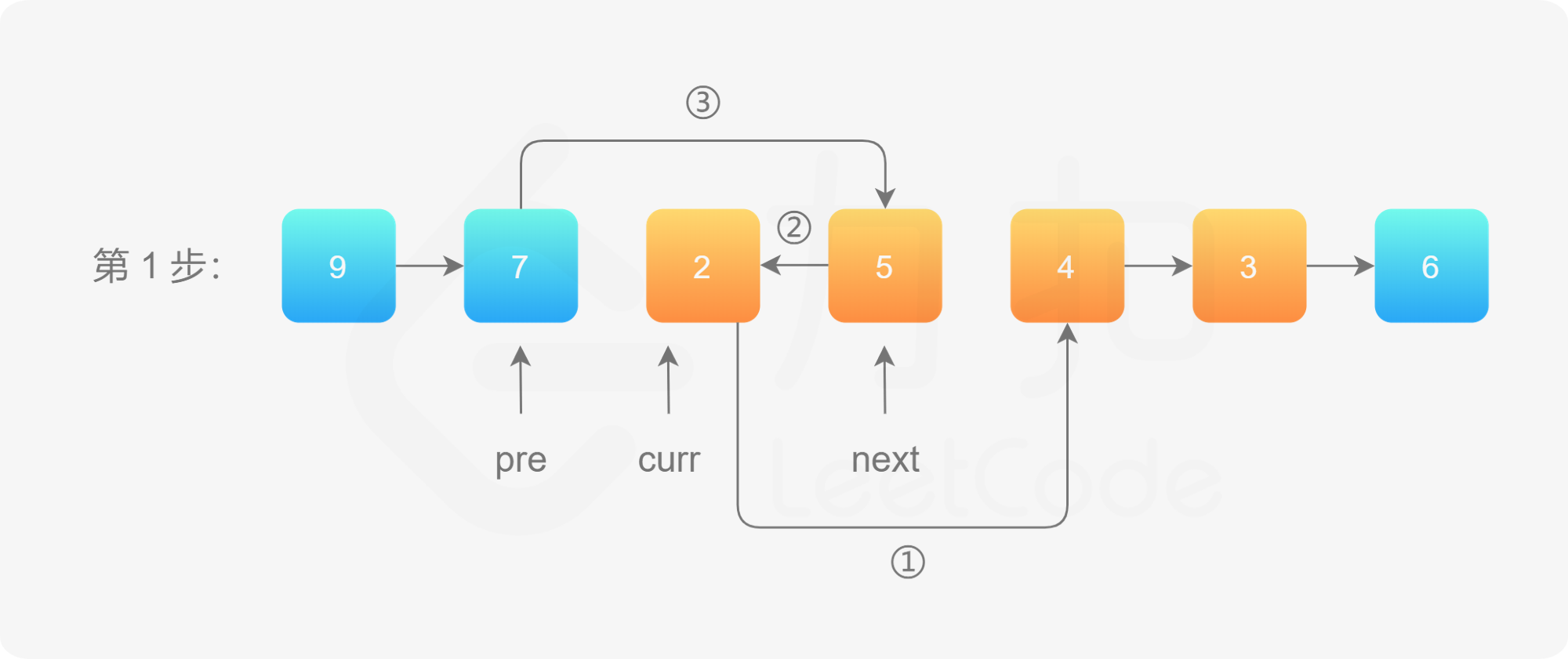
操作步骤:
先将 curr 的下一个节点记录为 next;
执行操作 ①:把 curr 的下一个节点指向 next 的下一个节点;
执行操作 ②:把 next 的下一个节点指向 pre 的下一个节点;
执行操作 ③:把 pre 的下一个节点指向 next。
第 1 步完成以后「拉直」的效果如下:
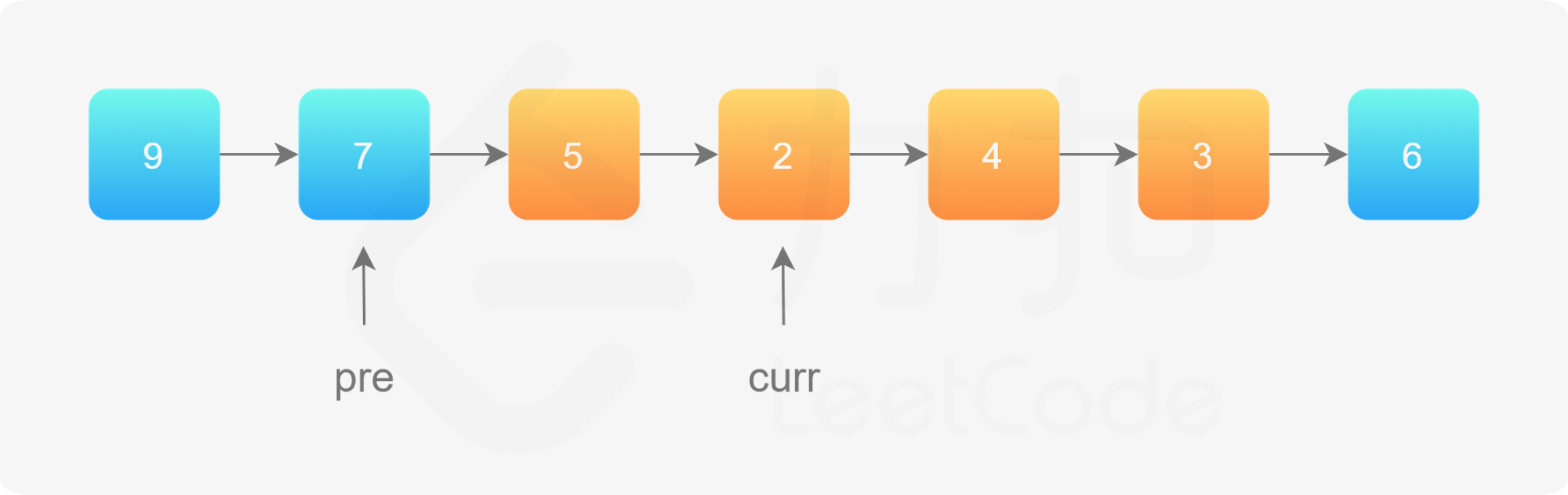
第 2 步,同理。同样需要注意 「穿针引线」操作的先后顺序。

第 2 步完成以后「拉直」的效果如下:
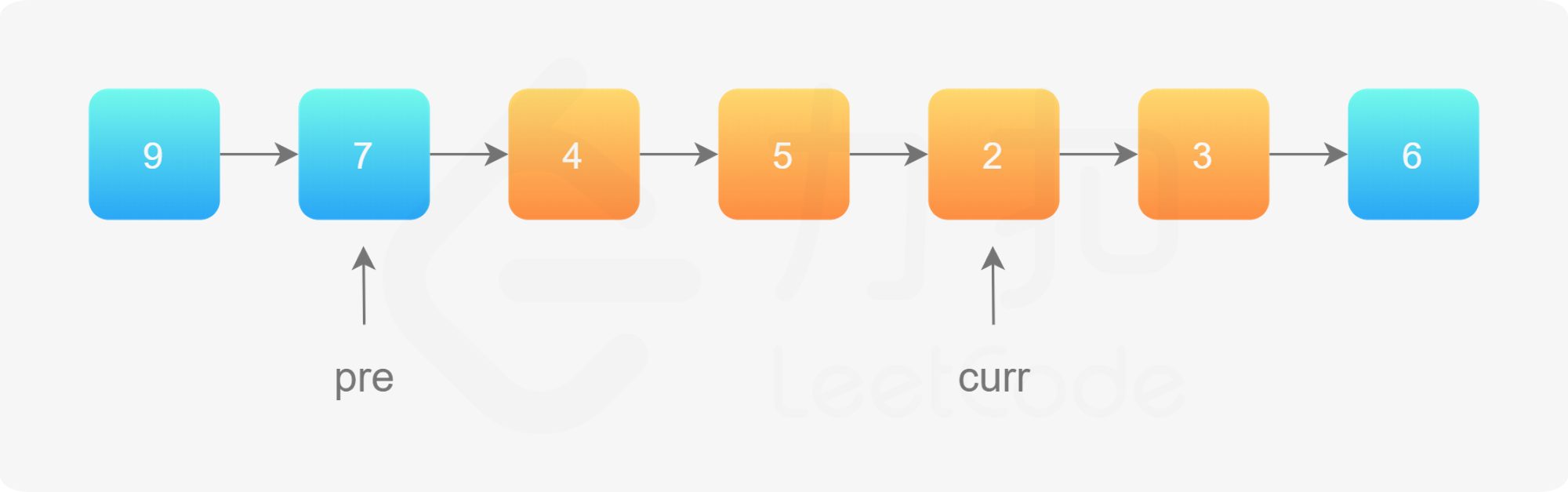
第 3 步,同理。
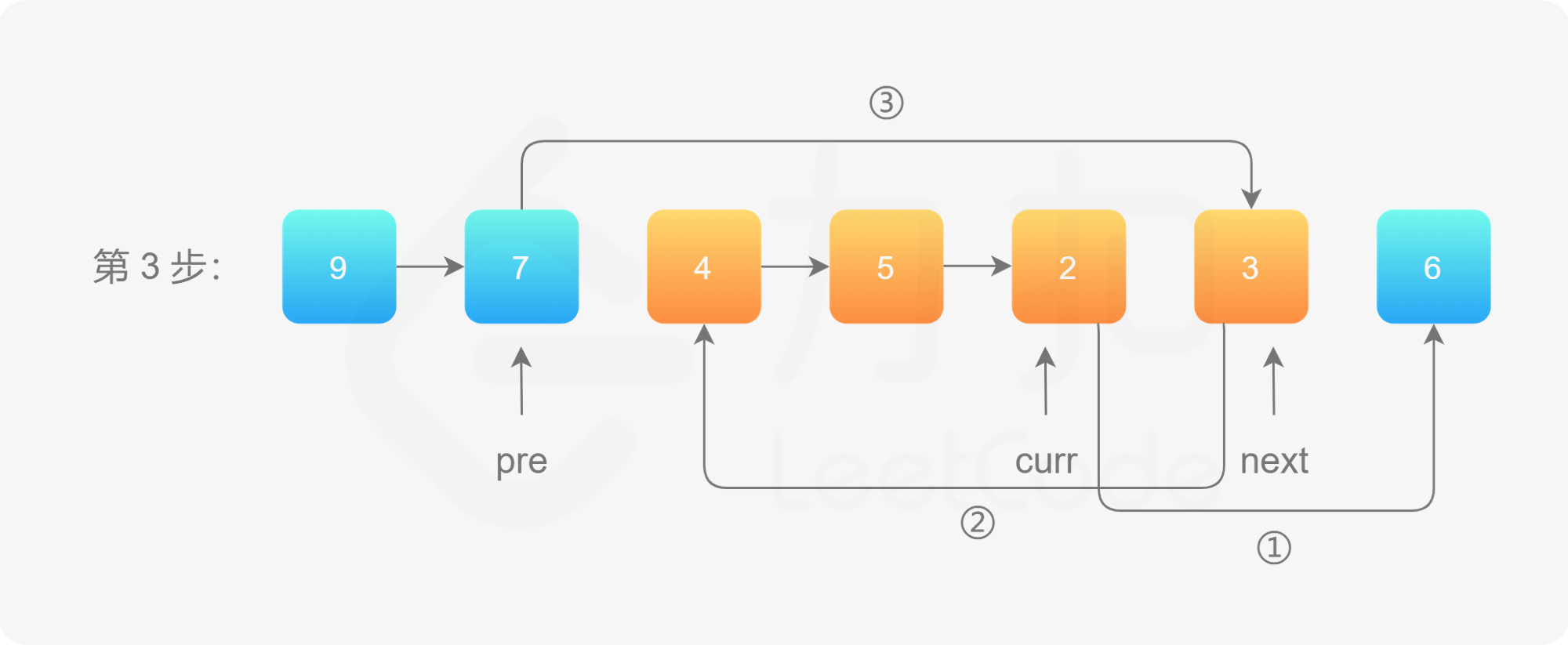
第 3 步完成以后「拉直」的效果如下:

代码如下:
1 ListNode* reverseBetween(ListNode* head, int left, int right) {
2 ListNode* vhead = new ListNode(-1);
3 vhead->next = head;
4 ListNode* tail = vhead;
5 int n = left;
6 while (tail && n > 1)
7 {
8 tail = tail->next;
9 n--;
10 }
11
12 ListNode* cur = tail->next;
13 for (int i = 0; i < right - left; i++)
14 {
15 ListNode* node = cur->next;
16
17 cur->next = node->next;
18 node->next = tail->next;
19 tail->next = node;
20 }
21
22 return vhead->next;
23 }
解法二:
整体思想就是将氛围三个部分,前面不需要反转的区域,需要反转的区域,后面不需要反转的区域。将需要反转的区域当作一个子串,进行反转,然后再将三部分进行拼接。
代码如下:
1 ListNode* ReverseList(ListNode* head)
2 {
3 if (head == nullptr || head->next == nullptr)
4 return head;
5
6 ListNode* vhead = new ListNode(-1);
7
8 while (head)
9 {
10 ListNode* node = head->next;
11 head->next = vhead->next;
12 vhead->next = head;
13 head = node;
14 }
15 return vhead->next;
16 }
17
18 ListNode *reverseBetween(ListNode *head, int left, int right) {
19 // 因为头节点有可能发生变化,使用虚拟头节点可以避免复杂的分类讨论
20 ListNode *vhead = new ListNode(-1);
21 vhead->next = head;
22
23 ListNode *pre = vhead;
24 // 第 1 步:从虚拟头节点走 left - 1 步,来到 left 节点的前一个节点
25 // 建议写在 for 循环里,语义清晰
26 for (int i = 0; i < left - 1; i++) {
27 pre = pre->next;
28 }
29
30 // 第 2 步:从 pre 再走 right - left + 1 步,来到 right 节点
31 ListNode *rightNode = pre;
32 for (int i = 0; i < right - left + 1; i++) {
33 rightNode = rightNode->next;
34 }
35
36 // 第 3 步:切断出一个子链表(截取链表)
37 ListNode *leftNode = pre->next;
38 ListNode *curr = rightNode->next;
39
40 // 注意:切断链接
41 pre->next = nullptr;
42 rightNode->next = nullptr;
43
44 // 第 4 步:同第 206 题,反转链表的子区间
45 leftNode = ReverseList(leftNode);
46
47 // 第 5 步:接回到原来的链表中
48 pre->next = rightNode;
49 leftNode->next = curr;
50 return vhead->next;
51 }
十三、链表排序
解决:

1 ListNode* MergeList(ListNode* left, ListNode* right) 2 { 3 if (left == nullptr) 4 return right; 5 if (right == nullptr) 6 return left; 7 8 if (left->val < right->val) 9 { 10 left->next = MergeList(left->next, right); 11 return left; 12 } 13 else 14 { 15 right->next = MergeList(left, right->next); 16 return right; 17 } 18 } 19 20 ListNode* FindMidListNode(ListNode* head) 21 { 22 ListNode* slow = head; 23 ListNode* fast = head; 24 25 while (fast && fast->next && fast->next->next) 26 { 27 slow = slow->next; 28 fast = fast->next->next; 29 } 30 return slow; 31 } 32 33 ListNode* sortList(ListNode* head) { 34 if (head == nullptr || head->next == nullptr) 35 return head; 36 37 ListNode* mid = FindMidListNode(head); 38 ListNode* newhead = mid->next; 39 mid->next = nullptr; 40 41 ListNode* head1 = sortList(head); 42 ListNode* head2 = sortList(newhead); 43 44 ListNode* thead = MergeList(head1, head2); 45 46 return thead; 47 }
十四、合并有序链表
题目链接:
https://leetcode-cn.com/problems/vvXgSW/
给定一个链表数组,每个链表都已经按升序排列。
请将所有链表合并到一个升序链表中,返回合并后的链表。
实例1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
解决:
1 /**
2 * Definition for singly-linked list.
3 * struct ListNode {
4 * int val;
5 * ListNode *next;
6 * ListNode() : val(0), next(nullptr) {}
7 * ListNode(int x) : val(x), next(nullptr) {}
8 * ListNode(int x, ListNode *next) : val(x), next(next) {}
9 * };
10 */
11 class Solution {
12 public:
13 ListNode* MergeList(ListNode* left, ListNode* right)
14 {
15 if (left == nullptr)
16 return right;
17 if (right == nullptr)
18 return left;
19
20 if (left->val < right->val)
21 {
22 left->next = MergeList(left->next, right);
23 return left;
24 }
25 else
26 {
27 right->next = MergeList(left, right->next);
28 return right;
29 }
30 }
31
32 ListNode* mergeKLists(vector<ListNode*>& lists) {
33 ListNode* ans = nullptr;
34 for(int i=0; i<lists.size(); i++)
35 {
36 ans = MergeList(ans, lists[i]);
37 }
38 return ans;
39 }
40 };
十五、回文链表
题目链接:
https://leetcode-cn.com/problems/aMhZSa/
给定一个链表的 头节点 head ,请判断其是否为回文链表。
如果一个链表是回文,那么链表节点序列从前往后看和从后往前看是相同的。
解决:
1 /**
2 * Definition for singly-linked list.
3 * struct ListNode {
4 * int val;
5 * ListNode *next;
6 * ListNode() : val(0), next(nullptr) {}
7 * ListNode(int x) : val(x), next(nullptr) {}
8 * ListNode(int x, ListNode *next) : val(x), next(next) {}
9 * };
10 */
11 class Solution {
12 public:
13 ListNode* FindMidListNode(ListNode* head)
14 {
15 ListNode* slow = head;
16 ListNode* fast = head;
17
18 while (fast && fast->next && fast->next->next)
19 {
20 slow = slow->next;
21 fast = fast->next->next;
22 }
23 return slow;
24 }
25
26 ListNode* ReverseLsit(ListNode* head)
27 {
28 if(head == nullptr || head->next == nullptr)
29 return head;
30
31 ListNode* vhead = new ListNode(-1);
32
33 while(head)
34 {
35 ListNode* node = head->next;
36 head->next = vhead->next;
37 vhead->next = head;
38 head = node;
39 }
40
41 return vhead->next;
42 }
43
44
45 bool isPalindrome(ListNode* head) {
46 if(head == nullptr || head->next == nullptr)
47 return head;
48 ListNode* mid = FindMidListNode(head);
49 ListNode* head1 = mid->next;
50 mid->next = nullptr;
51
52 head1 = ReverseLsit(head1);
53
54 while(head && head1)
55 {
56 if(head->val != head1->val)
57 return false;
58 head = head->next;
59 head1 = head1->next;
60 }
61
62 return true;
63 }
64 };
十六、复杂链表的复制
题目链接:
https://leetcode-cn.com/problems/LGjMqU/
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
解决:
1 class Solution {
2 public:
3 Node* copyRandomList(Node* head) {
4 if(head == nullptr)
5 return head;
6 unordered_map<Node*, Node*> reg;
7 Node* vhead = new Node(-1);
8 Node* tail = vhead;
9 Node* p = head;
10 while(p){
11 tail->next = new Node(p->val);
12 tail = tail->next;
13 reg[p] = tail;
14 p = p->next;
15 }
16
17 while(head){
18 if(head->random){
19 reg[head]->random = reg[head->random];
20 }
21 head = head->next;
22 }
23 return vhead->next;
24 }
25 };
十七、重排链表
题目链接:
https://leetcode-cn.com/problems/LGjMqU/
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln-1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln-1 → L2 → Ln-2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
解决:
1 class Solution {
2 public:
3 ListNode* FindMidListNode(ListNode* head)
4 {
5 ListNode* slow = head;
6 ListNode* fast = head;
7
8 while (fast && fast->next && fast->next->next)
9 {
10 slow = slow->next;
11 fast = fast->next->next;
12 }
13 return slow;
14 }
15
16 ListNode* ReverseLsit(ListNode* head)
17 {
18 if(head == nullptr || head->next == nullptr)
19 return head;
20
21 ListNode* vhead = new ListNode(-1);
22
23 while(head)
24 {
25 ListNode* node = head->next;
26 head->next = vhead->next;
27 vhead->next = head;
28 head = node;
29 }
30
31 return vhead->next;
32 }
33
34 void reorderList(ListNode* head) {
35 if(head == nullptr || head->next == nullptr)
36 return;
37
38 ListNode* mid = FindMidListNode(head);
39 ListNode* newhead = mid->next;
40 mid->next = nullptr;
41
42 newhead = ReverseLsit(newhead);
43
44 ListNode* node = head;
45 while(newhead)
46 {
47 ListNode* temp = newhead->next;
48
49 newhead->next = node->next;
50 node->next = newhead;
51
52 newhead = temp;
53
54 node = node->next->next;
55 }
56
57 }
58 };
参考文章
https://mp.weixin.qq.com/s/mFWLymqgmTf5gTvhpuXYBA
https://mp.weixin.qq.com/s/jJQTykI02oc5Hc6ObPFbmQ
本文来自博客园,作者:Mr-xxx,转载请注明原文链接:https://www.cnblogs.com/MrLiuZF/p/15225136.html


