Innodb B+树索引的分裂优化
一、B+树插入逻辑
1,如果结点不存在,则新生成一个结点,作为B+树的根结点,结束。
2,如果结点存在,则查找当前数值应该插入的位置,定位到需要插入到叶子结点,然后插入到叶子结点。
3,插入的结点如果未达到最大数量,结束。如果达到最大数量,则把当前叶子结点对半分裂:[m/2]个放入左结点,剩余放入右结点。
4,将分裂后到右结点的第一个值提升到父结点中。若父结点元素个数未达到最大,结束。若父结点元素个数达到最大,分裂父结点:[m/2]个元素分裂为左结点,m-[m/2]-1个分裂为右结点,第[m/2]+1个结点提升为父结点。
下面以实际操作讲解。为了演示,我们以3阶B+树为例。
1)插入结点5:B+树根结点不存在,生成根结点
2)插入结点8:根结点存在,查找存放结点为根结点,插入
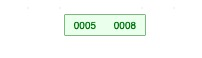
3)插入结点10 :同2)

结点元素个数达到最大3,分裂结点。([3/2]=)1个元素放左边,剩余2个元素放右边。并将右子结点的第一个值提升到父结点。
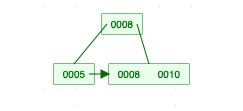
4)插入结点15 :找到插入到叶子结点,并插入,然后调整。步骤同3)

5)插入结点20 :步骤同3)
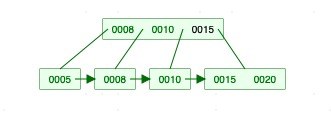
插入完成后,父结点元素个数达到最大,继续分裂父结点。([3/2]=)1个结点分裂为左结点;3-[3/2]-1=1个结点,分裂为右结点;第([3/2]+1=)2个结点提升为父结点。

二、mysql索引的B+树插入优化
以上就是B+树的插入逻辑。你应该已经发现,虽然B+树为3阶树,但是分裂后的叶子结点都只有1~2个。如果这个算法应用到数据库索引,假设一个磁盘分页可以存放2千条数据,但是每次分裂后,都只存储1000条数据在磁盘分页中,那么必然会造成磁盘浪费。而且时接近50%的浪费。B+树的这个设计,是因为插入的结点不是有序的,每次的插入,定位到每个叶子结点的可能性都是有的,所以采用对半分,防止叶子结点频繁分裂造成性能问题。但是索引值一般是自增数值,所以已经分裂过的叶子结点,后面是不会再有结点插入的。所以这部分的浪费是不可接受的。
出于以上考虑,mysql做了一版优化,即叶子结点在分裂时,不再按照对半分,而是保持原有的叶子结点不变,将超出的结点插入新的叶子结点,并把这个结点值,提升到父结点。父结点的分裂逻辑(待考证)。
但是,这样会引发新的问题。假如索引值是严格按照顺序插入的,那么没有问题,如果不是,就会引发更严重的空间浪费。
例如有下面一颗5阶B+树。

现在插入结点19,定位到左边叶子结点;插入后,该叶子结点达到最大值,然后分裂出新结点结点。

同理,继续插入结点18,同样会分裂出18的叶子结点。
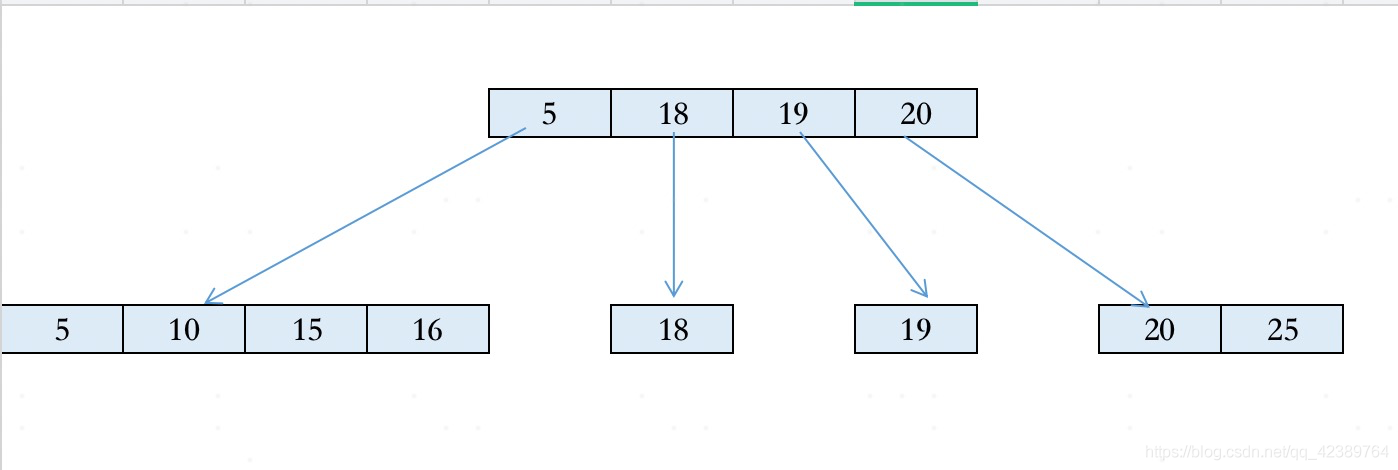
由于,18,19,20之间已经没有其他整型数值,所以18,19这两个结点永远都只有一个值,无疑带来了更严重的存储空间浪费。要知道,磁盘分页存储的可不是十几二十条记录。
然而,mysql团队很快也发现了这个问题,并在一次补丁中修复了该漏洞。详情可参见官方说明。
接下来,我们就用官方说明里面的方法,来验证现行的mysql索引的插入逻辑是怎么样的。
三、mysql的B+树插入逻辑
3.1 mysql版本
1 mysql> show variables like 'ver%';
2 +-------------------------+------------------------------+
3 | Variable_name | Value |
4 +-------------------------+------------------------------+
5 | version | 8.0.17 |
6 | version_comment | MySQL Community Server - GPL |
7 | version_compile_machine | x86_64 |
8 | version_compile_os | macos10.14 |
9 | version_compile_zlib | 1.2.11 |
10 +-------------------------+------------------------------+
11 5 行于数据集 (0.03 秒)
12
13 mysql>
3.2 新建测试表
1 CREATE TABLE test.page_split_test
2 (
3 id BIGINT UNSIGNED NOT NULL,
4 payload1 CHAR(255) NOT NULL,
5 payload2 CHAR(255) NOT NULL,
6 payload3 CHAR(255) NOT NULL,
7 payload4 CHAR(255) NOT NULL,
8 PRIMARY KEY (`id`)
9 ) ENGINE=INNODB;
3.3 填充B+树根结点
填充根结点至分裂前的最大值
1 # Fill up the root page, but don't split it.
2
3 INSERT INTO test.page_split_test (id, payload1, payload2, payload3, payload4)
4 VALUES
5 (1, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
6 (2, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
7 (3, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
8 (4, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
9 (5, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
10 (6, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
11 (7, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
12 (8, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
13 (9, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
14 (10, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
15 (11, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
16 (12, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
17 (13, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
18 (14, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255));
查看B+树结点情况
1 SELECT page_number, page_type, number_records, data_size
2 FROM information_schema.innodb_buffer_page
3 WHERE table_name like "%page_split_test%" AND index_name = "PRIMARY";
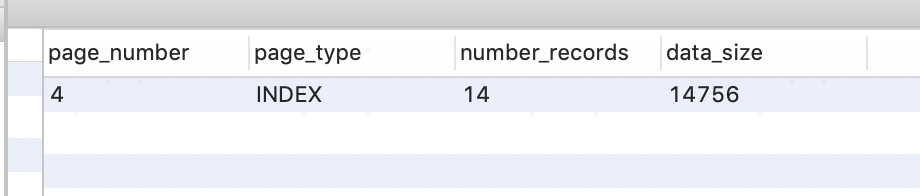
结果如下,当前只有一个根结点,含14个数据行
3.4 首次分裂
继续插入一个数据,B+树达到最大,首次进行分裂。
1 INSERT INTO test.page_split_test (id, payload1, payload2, payload3, payload4)
2 VALUES (15, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255));
查看B+树结点情况如下
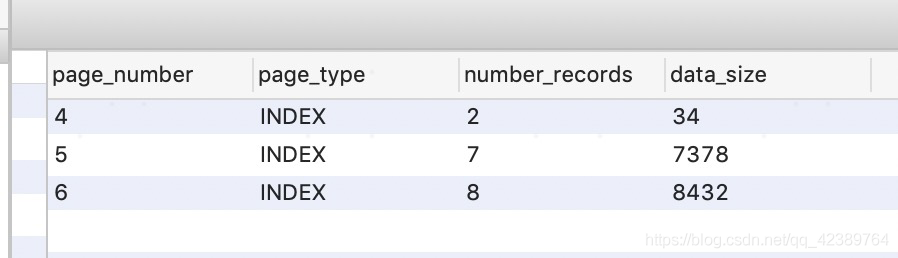

根结点对半分裂成两个结点,左结点(第5页)和右结点(第6页),原来的根结点(第4页)升级为父结点,父结点中包含两个元素,分别为指向两个子结点的引用。
3.5 继续填充右叶子结点
继续插入数据,填充右叶子结点至临近饱和状态。
1 INSERT INTO test.page_split_test (id, payload1, payload2, payload3, payload4)
2 VALUES
3 (16, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
4 (17, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
5 (18, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
6 (19, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
7 (20, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255)),
8 (21, REPEAT("A", 255), REPEAT("B", 255), REPEAT("C", 255), REPEAT("D", 255));
查看B+树状态
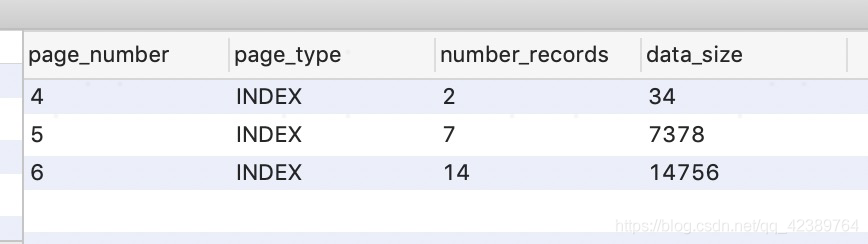
在这里,mysql并没有像之前的bug一样,生成6个结点,而是将后面的6个结点合并成了一个。这就是mysql做的再一次优化,即叶子结点满了之后,如果该叶子结点后面有还有叶子结
点,则会将新的数据插入到后续的叶子结点中。
然而这样的方案,虽然避免了空间浪费,但是增加了索引插入时的性能。极端假设,新增的数据定位到了第一个叶子结点,插入后,叶子结点达到最大数量,然后分裂出最后的一个元素插到后一个叶子结点。假设后面的叶子结点都是已经满额的状态,那么这个插入会导致所有的叶子结点都发生一次分裂,且所有父结点的数据都要重新调整。这样的效率简直是灾难性的。
然而,这个问题,可以通过人为的避免,那就是使用自增索引。自增索引,可以保证每次插入的主键都是递增的,永远都只会修改和新增最右的叶子结点,而不用修改原有叶子结点。所以,使用递增索引,可以大大提升数据的插入效率。
四、mysql的B+树插入逻辑小结
InnoDB的索引分裂策略,在特定的情况下,索引页面的分裂存在问题,导致每个分裂出来的页面,仅仅存储一条记录,页面的空间利用率极低。
4.1 B+树的分裂
传统B+树页面分裂操作分析:
按照原页面中50%的数据量进行分裂,针对当前这个分裂操作,3,4记录保留在原有页面,5,6记录,移动到新的页面。最后将新纪录7插入到新的页面中;
50%分裂策略的优势:
分裂之后,两个页面的空间利用率是一样的;如果新的插入是随机在两个页面中挑选进行,那么下一次分裂的操作就会更晚触发;
50%分裂策略的劣势:
空间利用率不高:按照传统50%的页面分裂策略,索引页面的空间利用率在50%左右;
分裂频率较大:针对如上所示的递增插入(递减插入),每新插入两条记录,就会导致最右的叶页面再次发生分裂;
4.2 B+树分裂操作的优化
新的分裂策略,在插入7时,不移动原有页面的任何记录,只是将新插入的记录7写到新页面之中;原有页面的利用率,仍旧是100%;
优化分裂策略的优势:
索引分裂的代价小:不需要移动记录;
索引分裂的概率降低:如果接下来的插入,仍旧是递增插入,那么需要插入4条记录,才能再次引起页面的分裂。相对于50%分裂策略,分裂的概率降低了一半;
索引页面的空间利用率提高:新的分裂策略,能够保证分裂前的页面,仍旧保持100%的利用率,提高了索引的空间利用率;
优化分裂策略的劣势:
如果新的插入,不再满足递增插入的条件,而是插入到原有页面,那么就会导致原有页面再次分裂,增加了分裂的概率。
因此,此优化分裂策略,仅仅是针对递增递减插入有效,针对随机插入,就失去了优化的意义,反而带来了更高的分裂概率。
在InnoDB的实现中,为每个索引页面维护了一个上次插入的位置,以及上次的插入是递增/递减的标识。根据这些信息,InnoDB能够判断出新插入到页面中的记录,是否仍旧满足递增/递减的约束,若满足约束,则采用优化后的分裂策略;若不满足约束,则退回到50%的分裂策略。
五、参考文章
https://blog.csdn.net/baidu_29258265/article/details/82150728?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-4.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-4.control
https://blog.csdn.net/qq_42389764/article/details/108152624
本文来自博客园,作者:Mr-xxx,转载请注明原文链接:https://www.cnblogs.com/MrLiuZF/p/15169695.html

