二叉树顺序存储之 前序，中序 ，后序遍历

二叉树遍历的概念：

　　二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次且仅被访问一次。

 

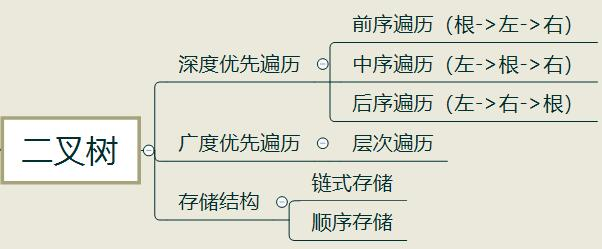
二叉树的深度优先遍历可细分为前序遍历、中序遍历、后序遍历，这三种遍历可以用递归实现

　　前序遍历：根节点->左子树->右子树（根->左->右）

　　中序遍历：左子树->根节点->右子树（左->根->右）

　　后序遍历：左子树->右子树->根节点（左->右->根）

前序遍历

1）依据上文提到的遍历思路：根结点 ---> 左子树 ---> 右子树，非常easy写出递归版本号：

/* 以递归方式 前序遍历二叉树 */
void PreOrderTraverse(BiTree t, int level)
{
    if (t)
    {

　　 　　printf("data = %c level = %d\n ", t->data, level);
    　　PreOrderTraverse(t->lchild, level + 1);
    　　PreOrderTraverse(t->rchild, level + 1);

   } 

2）如今讨论非递归的版本号：

　　依据前序遍历的顺序，优先訪问根结点。然后在訪问左子树和右子树。所以。对于随意结点node。第一部分即直接訪问之，之后在推断左子树是否为空，不为空时即反复上面的步骤，直到其为空。若为空。则须要訪问右子树。注意。在訪问过左孩子之后。须要反过来訪问其右孩子。所以，须要栈这样的数据结构的支持。对于随意一个结点node，详细过程例如以下：

a)訪问之，并把结点node入栈。当前结点置为左孩子；

b)推断结点node是否为空，若为空。则取出栈顶结点并出栈，将右孩子置为当前结点；否则反复a)步直到当前结点为空或者栈为空（能够发现栈中的结点就是为了訪问右孩子才存储的）

代码例如以下：

public void preOrderTraverse2(TreeNode root) {  
        Stack<TreeNode> stack = new Stack<>();  
        TreeNode pNode = root;  
        while (pNode != null || !stack.isEmpty()) {  
            if (pNode != null) {  
                System.out.print(pNode.val+"  ");  
                stack.push(pNode);  
                pNode = pNode.left;  
            } else { //pNode == null && !stack.isEmpty()  
                TreeNode node = stack.top();  
　　　　　　　　　 stack.pop();
                pNode = node.right;  
            }  
        }  
    }

 

 

 

 

 

 

 

中序遍历

1)依据上文提到的遍历思路：左子树 ---> 根结点 ---> 右子树，非常easy写出递归版本号：

/* 以递归方式 中序遍历二叉树 */
void PreOrderTraverse(BiTree t, int level)
{
    if (t == NULL)
    {

　　 　　PreOrderTraverse(t->lchild, level + 1);
    　　printf("data = %c level = %d\n ", t->data, level);
    　　PreOrderTraverse(t->rchild, level + 1);

 　　} 
}

2）非递归实现，有了上面前序的解释，中序也就比較简单了。同样的道理。仅仅只是訪问的顺序移到出栈时。代码例如以下：

public void inOrderTraverse2(TreeNode root) {  
        Stack<TreeNode> stack = new Stack<>();  
        TreeNode pNode = root;  
        while (pNode != null || !stack.isEmpty()) {  
            if (pNode != null) {  
                stack.push(pNode);  
                pNode = pNode.left;  
            } else { //pNode == null && !stack.isEmpty()  
                TreeNode node = stack.top();
　　　　　　　　   stack.pop();  
                System.out.print(node.val+"  ");  
                pNode = node.right;  
            }  
        }  
    }

 

后序遍历

1）依据上文提到的遍历思路：左子树 ---> 右子树 ---> 根结点。非常easy写出递归版本号：

/* 以递归方式 后序遍历二叉树 */
void PreOrderTraverse(BiTree t, int level)
{
    if (t)
    {
    　　PreOrderTraverse(t->lchild, level + 1);
    　　PreOrderTraverse(t->rchild, level + 1);
    　　printf("data = %c level = %d\n ", t->data, level);
　　 }
}

2）后序遍历的非递归实现是三种遍历方式中最难的一种。由于在后序遍历中，要保证左孩子和右孩子都已被訪问而且左孩子在右孩子前訪问才干訪问根结点，这就为流程的控制带来了难题。以下介绍两种思路。

      第一种思路：对于任一结点P，将其入栈，然后沿其左子树一直往下搜索。直到搜索到没有左孩子的结点，此时该结点出在栈顶，可是此时不能将其出栈并訪问，因此其右孩子还未被訪问。

所以接下来依照同样的规则对其右子树进行同样的处理，当訪问完其右孩子时。该结点又出在栈顶，此时能够将其出栈并訪问。这样就保证了正确的訪问顺序。能够看出，在这个过程中，每一个结点都两次出在栈顶，仅仅有在第二次出如今栈顶时，才干訪问它。因此须要多设置一个变量标识该结点是否是第一次出如今栈顶。

void postOrder2(BinTree *root)    //非递归后序遍历
{
    stack<BTNode*> s;
    BinTree *p=root;
    BTNode *temp;
    while(p!=NULL||!s.empty())
    {
        while(p!=NULL)              //沿左子树一直往下搜索。直至出现没有左子树的结点 
        {
            BTNode *btn=(BTNode *)malloc(sizeof(BTNode));
            btn->btnode=p;
            btn->isFirst=true;
            s.push(btn);
            p=p->lchild;
        }
        if(!s.empty())
        {
            temp=s.top();
            s.pop();
            if(temp->isFirst==true)     //表示是第一次出如今栈顶 
             {
                temp->isFirst=false;
                s.push(temp);
                p=temp->btnode->rchild;    
            }
            else                        //第二次出如今栈顶 
             {
                cout<<temp->btnode->data<<" ";
                p=NULL;
            }
        }
    }    
}

另外一种思路：要保证根结点在左孩子和右孩子訪问之后才干訪问，因此对于任一结点P。先将其入栈。假设P不存在左孩子和右孩子。则能够直接訪问它；或者P存在左孩子或者右孩子。可是其左孩子和右孩子都已被訪问过了。则相同能够直接訪问该结点。若非上述两种情况。则将P的右孩子和左孩子依次入栈。这样就保证了每次取栈顶元素的时候，左孩子在右孩子前面被訪问。左孩子和右孩子都在根结点前面被訪问。

void postOrder3(BinTree *root)     //非递归后序遍历
{
    stack<BinTree*> s;
    BinTree *cur;                      //当前结点 
    BinTree *pre=NULL;                 //前一次訪问的结点 
    s.push(root);
    while(!s.empty())
    {
        cur=s.top();
        if((cur->lchild==NULL&&cur->rchild==NULL)||
           (pre!=NULL&&(pre==cur->lchild||pre==cur->rchild)))
        {
            cout<<cur->data<<" ";  //假设当前结点没有孩子结点或者孩子节点都已被訪问过 
              s.pop();
            pre=cur; 
        }
        else
        {
            if(cur->rchild!=NULL)
                s.push(cur->rchild);
            if(cur->lchild!=NULL)    
                s.push(cur->lchild);
        }
    }    
}

 

三种递归遍历方式对应的代码几乎相同，只是一条语句的位置发生了变化

printf("data = %c level = %d\n ", t->data, level);

　　只看文字和代码来理解遍历的过程是比较困难的，建议读者亲自去遍历，为了理清遍历的过程下面上题

 

 

 

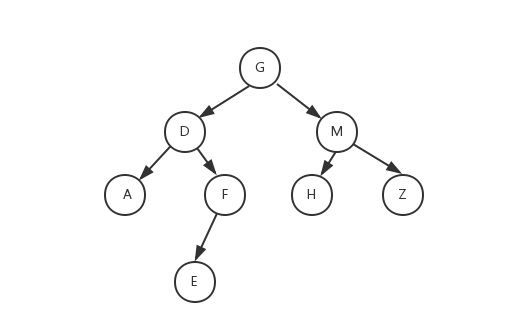
前序遍历

前序的遍历的特点，根节点->左子树->右子树，注意看前序的遍历的代码printf语句是放在两条递归语句之前的，所以先访问根节点G，打印G，然后访问左子树D，此时左子树D又作为根节点，打印D，再访问D的左子树A

A又作为根节点，打印A，A没有左子树或者右子树，函数调用结束返回到D节点（此时已经打印出来的有：GDA）D节点的左子树已经递归完成，现在递归访问右子树F，F作为根节点，打印F，F有左子树访问左子树E，E作为

根节点，打印E，（此时已经打印出来的有：GDAFE），E没有左子树和右子树，函数递归结束返回F节点，F的左子树已经递归完成了，但没有右子树，所以函数递归结束，返回D节点，D节点的左子树和右子树递归全部完成，

函数递归结束返回G节点，访问G节点的右子树M，M作为根节点，打印M，访问M的左子树H，H作为根节点，打印H，（此时已经打印出来的有：GDAFEMH）H没有左子树和右子树，函数递归结束，返回M节点，M节点的左子树已经

递归完成，访问右子树Z，Z作为根节点，打印Z，Z没有左子树和右子树，函数递归结束，返回M节点，M节点的左子树右子树递归全部完成，函数递归结束，返回G节点，G节点的左右子树递归全部完成，整个二叉树的遍历就结束了

（MGJ，终于打完了··）

前序遍历结果：GDAFEMHZ

 

总结一下前序遍历步骤

第一步：打印该节点（再三考虑还是把访问根节点这句话去掉了）

第二步：访问左子树，返回到第一步（注意：返回到第一步的意思是将根节点的左子树作为新的根节点，就好比图中D是G的左子树但是D也是A节点和F节点的根节点）

第三步：访问右子树，返回到第一步

第四步：结束递归，返回到上一个节点

 前序遍历的另一种表述：

（1）访问根节点

（2）前序遍历左子树

（3）前序遍历右子树

（在完成第2,3步的时候，也是要按照前序遍历二叉树的规则完成）

前序遍历结果：GDAFEMHZ

 

中序遍历

中序遍历步骤

第一步：访问该节点左子树

第二步：若该节点有左子树，则返回第一步，否则打印该节点

第三步：若该节点有右子树，则返回第一步，否则结束递归并返回上一节点

（按我自己理解的中序就是：先左到底，左到不能在左了就停下来并打印该节点，然后返回到该节点的上一节点，并打印该节点，然后再访问该节点的右子树，再左到不能再左了就停下来）

中序遍历的另一种表述：

（1）中序遍历左子树

（2）访问根节点

（3）中序遍历右子树

（在完成第1，3步的时候，要按照中序遍历的规则来完成）

所以该图的中序遍历为：ADEFGHMZ

 

后序遍历步骤

第一步：访问左子树

第二步：若该节点有左子树，返回第一步

第三步：若该节点有右子树，返回第一步，否则打印该节点并返回上一节点

 后序遍历的另一种表述：

（1）后序遍历左子树

（2）后序遍历右子树

（3）访问根节点

（在完成1,2步的时候，依然要按照后序遍历的规则来完成）

该图的后序遍历为：AEFDHZMG

 （读者如果在纸上遍历二叉树的时候，仍然容易将顺序搞错建议再回去看一下三种不同遍历对应的代码）

进入正题，已知两种遍历结果求另一种遍历结果（其实就是重构二叉树）

第一种：已知前序遍历、中序遍历求后序遍历

前序遍历：ABCDEF

中序遍历：CBDAEF

在进行分析前读者需要知道不同遍历结果的特点

1、前序遍历的第一元素是整个二叉树的根节点

2、中序遍历中根节点的左边的元素是左子树，根节点右边的元素是右子树

3、后序遍历的最后一个元素是整个二叉树的根节点

（如果读者不明白上述三个特点，建议再回去看一下三种不同遍历对应的代码，并在纸上写出一个简单的二叉树的三种不同的遍历结果，以加深对三种不同遍历的理解）

用上面这些特点来分析遍历结果，

 

 

 第一步先看前序遍历A肯定是根节点

第二步：确认了根节点，再来看中序遍历，中序遍历中根节点A的左边是CBD，右边是EF，所有可以确定二叉树既有左子树又有右子树

 

 

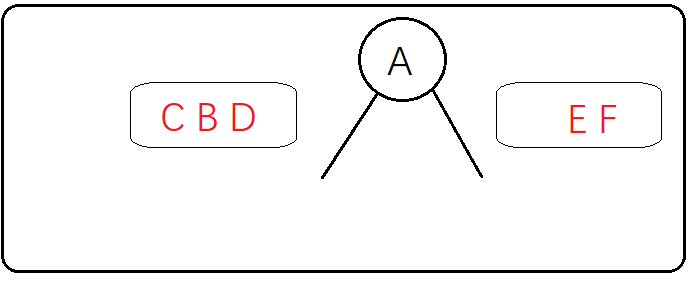
 第三步：先来分析左子树CBD，那么CBD谁来做A的左子树呢？这个时候不能直接用中序遍历的特点（左->根->右）得出左子树应该是这个样子

 

 

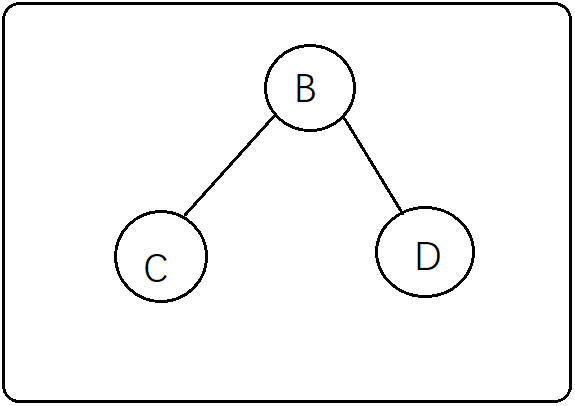
 因为有两种情况都满足中序遍历为CBD

 

 

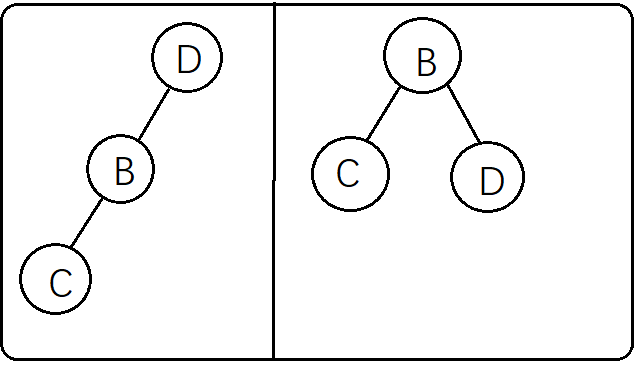
直接根据中序遍历来直接得出左子树的结构，这个时候就要返回到前序遍历中去

观察前序遍历ABCDEF，左子树CBD在前序遍历中的顺序是BCD，意味着B是左子树的根节点（这么说可能不太好理解，换个说法就是B是A的左子树）,得出这个结果是因为如果一个二叉树的根节点有左子树，那么

这个左子树一定在前序遍历中一定紧跟着根节点（这个是用前序遍历的特点（根->左->右）得出的）,到这里就可以确认B是左子树的根节点

　　

 

 第四步：再观察中序遍历CBDAEF，B元素左边是C右边是D，说明B节点既有左子树又有右子树，左右子树只有一个元素就可以直接确定了，不用再返回去观察前序遍历

 

 

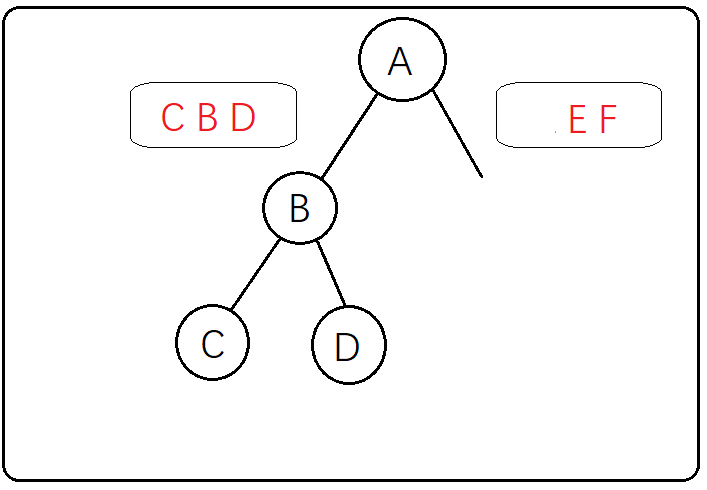
第五步：到这里左子树的重建就已经完成了，现在重建右子树，因为重建右子树的过程和左子树的过程一模一样，步骤就不像上面写这么细了（(┬＿┬)），观察中序遍历右子树为EF，再观察前序遍历ABCDEF中右子树

的顺序为EF，所以E为A的右子树，再观察中序便利中E只有右边有F，所有F为E的右子树，最后得到的二叉树是这个样子的

 

 

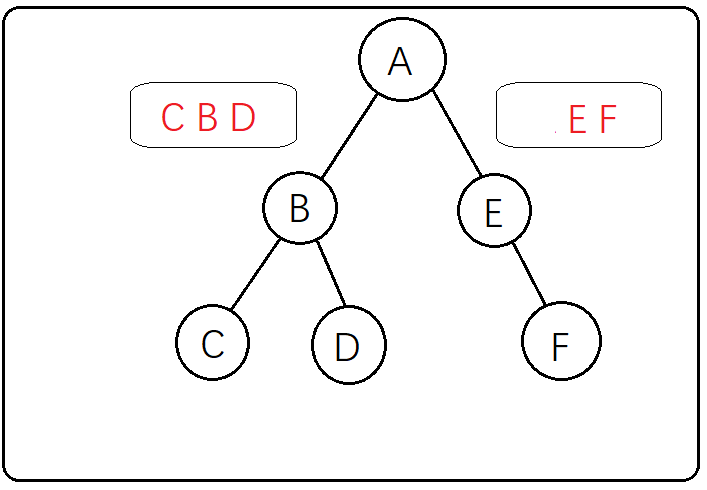
所有求得的后序遍历为：CDBFEA

 

总结一下上述步骤： 先观察前序遍历找到根节点->观察中序遍历将根节点左边归为左子树元素，右边归为右子树元素（可能会出现只有左子树或者右子树的情况）->观察前序遍历中左\右子树几个元素的顺序，最靠前的为左\右子树的根节点->重复前面的步骤

第二种：已知中序遍历、后序遍历求前序遍历（题还是上面这道）

中序遍历：CBDAEF

后序遍历为：CDBFEA

仍然是根据不同遍历方式结果的特点来重构二叉树，过程很相似这里就不详细说了，后序遍历的最后一个元素A是根节点，在中序遍历中以根节点A作为分界将元素分为左子树（CBD）和右子树（EF），再观察后序遍历中左子树的顺序是CDB

，可以判断出B是左子树的根节点（因为后序遍历是：左->右->根），再观察中序遍历，B元素左边是C右边是D，说明B节点既有左子树又有右子树，左右子树只有一个元素就可以直接确定了，不用再返回去观察后序遍历，左子树重建完成，

现在来看右子树，右子树有两个元素EF，观察后序遍历E在F的后面，所以E是右子树的根节点，然后看中序遍历中E只有右边一个F元素了，即F是E的右子树，此时整个二叉树重构完成

 

总结一下上述步骤：先观察后序遍历找到根节点->观察中序遍历将根节点左边归为左子树元素，右边归为右子树元素（可能会出现只有左子树或者右子树的情况）->观察后序遍历中左\右子树几个元素的顺序，最靠后的为左\右子树的根节点->重复前面的步骤

 

注意：已知前序遍历、后序遍历无法求出中序遍历（因为由前序后序重构出来的二叉树不止一种）

举个栗子

 

 

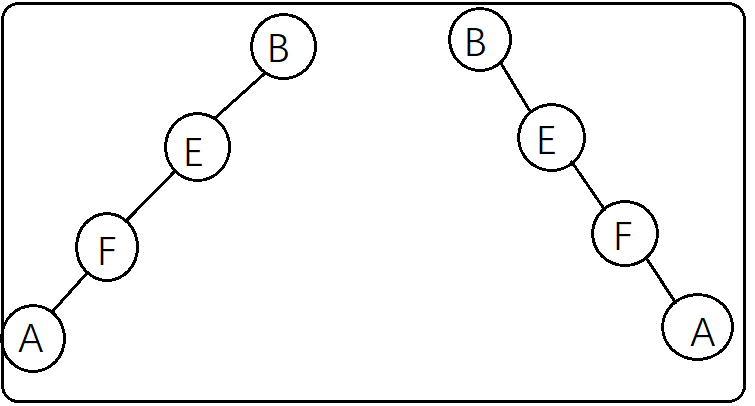
左图这两种二叉树前序（BEFA）和后序（AFEB）一样，但对应的中序遍历结果不一样（左边的是AFEB右边的是BEFA），所以仅靠前序后序是

重构出唯一的二叉树

层序遍历

 

 

层序遍历。听名字也知道是按层遍历。我们知道一个节点有左右节点。而每一层一层的遍历都和左右节点有着很大的关系。也就是我们选用的数据结构不能一股脑的往一个方向钻，而左右应该均衡考虑。这样我们就选用队列来实现。

• 对于队列，现进先出。从根节点的节点push到队列，那么队列中先出来的顺序是第二层的左右(假设有)。第二层每个执行的时候添加到队列，那么添加的所有节点都在第二层后面。
• 同理，假设开始pop遍历第n层的节点，每个节点会push左右两个节点进去。但是队列先进先出。它会放到队尾(下一层)。直到第n层的最后一个pop出来，第n+1层的还在队列中整齐排着。这就达到一个层序的效果。

实现的代码也很容易理解：

public void LevelOrder(node t) {//层序遍历
    Queue<node> q1 = new ArrayDeque<node>();
    if (t == null)
        return;
    if (t != null) {
        q1.add(t);
    }
    while (!q1.isEmpty()) {
        node t1 = q1.poll();
        if (t1.left != null)
            q1.add(t1.left);
        if (t1.right != null)
            q1.add(t1.right);
        System.out.print(t1.value + " ");
    }
    System.out.println();
}