1477B - Nezzar and Binary String 1900
题目来源
https://codeforces.ml/problemset/problem/1477/B
题意分析
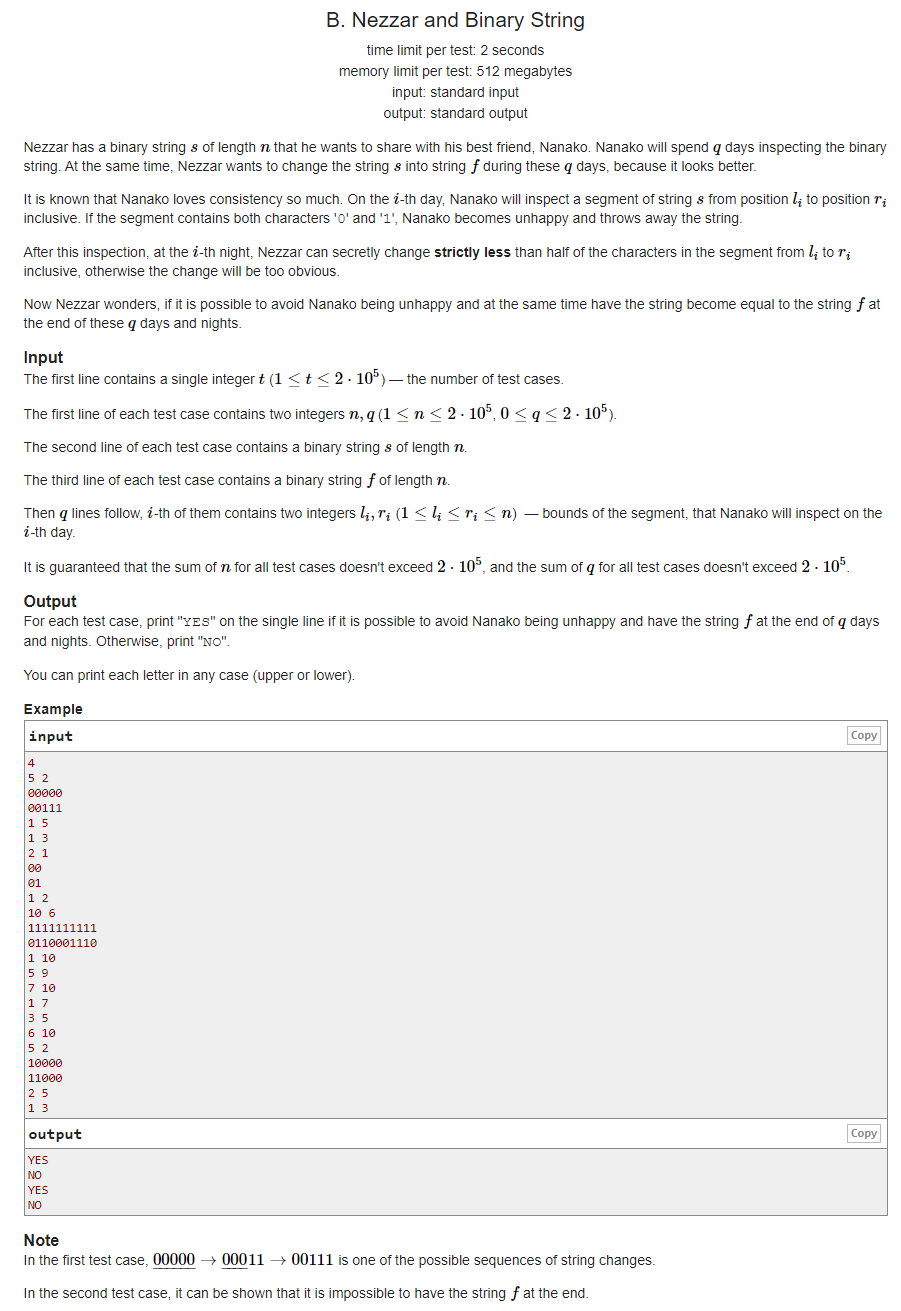
给定两个长度为n的01序列,分别表示a,b。再给定一个q,表示有q个询问区间。在保证每次询问中,区间内所有数字相同的情况下, 可以修改严格小于区间长度一半的数。问在q次操作之后,能否实现将a序列变成b序列。
思路分析
对于q个询问区间进行逆序操作。根据n和q的数据范围来看,因为q次询问必须遍历,所以最后的时间复杂度可能是O(qlogn)。于是就有了用线段树维护区间和来解决区间01覆盖的问题,一次覆盖就是一个区间修改。最后判断所有操作后的最终序列是否与a序列相同即可。
code
#include <bits/stdc++.h> #define ll long long #define INF 0x3f3f3f3f using namespace std; const int maxn = 2e5 + 7; int a[maxn], b[maxn]; int tr[maxn << 2], lz[maxn << 2]; int ql[maxn], qr[maxn]; int pre[maxn]; void build(int k, int l, int r){ if (l == r){ lz[k] = -1; tr[k] = b[l]; return; } int mid = l + r >> 1; build(k<<1, l, mid); build(k<<1|1, mid+1, r); tr[k] = tr[k<<1] + tr[k<<1|1]; lz[k] = -1; } void pushdown(int k, int l, int r, int mid){ if (lz[k] == -1) return; if (lz[k]){ lz[k<<1] = 1; lz[k<<1|1] = 1; tr[k<<1] = mid - l + 1; tr[k<<1|1] = r - mid; }else{ lz[k<<1] = 0; lz[k<<1|1] = 0; tr[k<<1] = 0; tr[k<<1|1] = 0; } lz[k] = -1; } void update(int k, int l, int r, int L, int R, int x){ if (L <= l && r <= R){ lz[k] = x; tr[k] = x * (r - l + 1); return; } int mid = l + r >> 1; pushdown(k, l, r, mid); if (L <= mid) update(k<<1, l, mid, L, R, x); if (mid < R) update(k<<1|1, mid+1, r, L, R, x); tr[k] = tr[k << 1] + tr[k << 1 | 1]; } int sum(int k, int l, int r, int L, int R){ if (L <= l && r <= R) return tr[k]; int mid = l + r >> 1; pushdown(k, l, r, mid); int ans = 0; if (L <= mid) ans += sum(k<<1, l, mid, L, R); if (mid < R) ans += sum(k<<1|1, mid+1, r, L, R); return ans; } int main(){ int t; scanf("%d", &t); while (t --){ int n, q; scanf("%d%d", &n, &q); for (int i=1; i<=n; i++) scanf("%1d", &a[i]); for (int i=1; i<=n; i++) scanf("%1d", &b[i]); for (int i=1; i<=n; i++) pre[i] = pre[i-1] + a[i]; build(1, 1, n); for (int i=1; i<=q; i++) scanf("%d%d", &ql[i], &qr[i]); bool flag = false; for (int i=q; i>=1; i--){ int l = ql[i], r = qr[i]; int one = sum(1, 1, n, l, r), zero = r - l + 1 - one; // cout << "l: " << l << " r:" << r << " one: " << one << " " << zero << endl; if (one == zero){ // cout << "nei" << endl; flag = true; break; } if (one > zero) update(1, 1, n, l, r, 1); else update(1, 1, n, l, r, 0); } if (flag){ printf("NO\n"); continue; } for (int i=1; i<=n; i++){ int one = sum(1, 1, n, 1, i); if (one != pre[i]){ // cout << "i: " << i << " one: " << one << endl; flag = true; break; } } if (flag) printf("NO\n"); else printf("YES\n"); } return 0; }


