F - Zebraness (Caddi Programming Contest 2021(AtCoder Beginner Contest 193))
题目来源
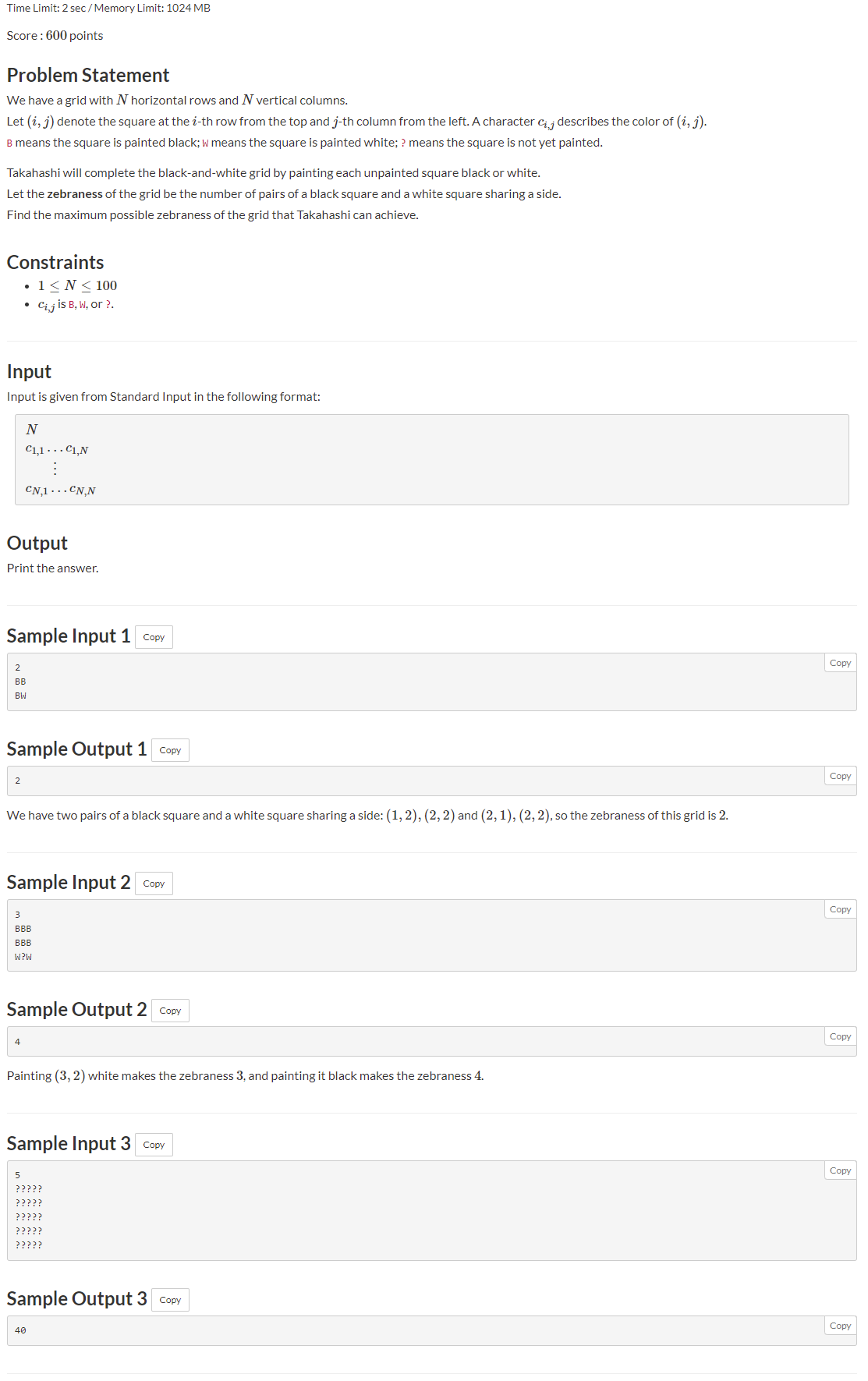
https://atcoder.jp/contests/abc193/tasks/abc193_f
题意分析
给出一个二维的表格,每一个格子上有一个字符表示当前格子上面的颜色。‘W’表示白色,‘B’表示黑色,‘?’表示还没有上色。求当给所有未上色的格子上色之后,白色与黑色格子相邻的边最大的数量。
思路分析
看到黑白两种颜色之后,比较容易想到的是二分图,进而想到网络流。而最后可以将问题化为最小割的问题,这也是官方题解。
可以想到的是,将所有黑色的格子和白色的格子分成二分图的两边,还没有染色的格子就放在中间,将相邻的格子都进行连边即可。这样去跑网络流,我们最后得到的是这张图那类边最小的数量。在官方题解中,将i+j分成奇偶两个部分,并将其中一个部分的黑白颠倒(即黑变白,白变黑),然后再跑网络流,得出的结果就是最小割。表格总共有2 * n * (n-1)的边,减去之后就是最终的答案。
回想这个过程,可以想清楚的是将奇偶分开是因为只有奇偶的格子之间连边,而进行颜色颠倒的一个原因是,当我们使用二分图将黑色和白色的格子分开的时候,黑色边与黑色边的连边并不能形成一条有效的增广路,而我们的目的是为了将这些相同相邻颜色的格子之间的边去掉,所以当颠倒之后,就很自然的分到了两边去。
最后最终要的是,问题是如何转换成最小割问题的。对于这样的问题,当我们想到分成二分图的时候,我们肯定会想到一个阶段,即这个最大值的数量在计数的时候到底是正着计数还是倒着计数(即去掉不符合条件的边)。而在本题之中,如果选择正着计数的话,那就是相邻的两个格子颜色不同时会对我们的答案有贡献,但在这种条件下直接跑网络流会出错。最后究其原因,个人以为是在某些无法流通的边下,仍然存在可以被记入答案的贡献边。最简单的例子是一个只含有黑色和未涂色的二维表格。整张网络流是没有流量的,但是当我们将未涂色的格子填上白色之后其实就可以跑通了。(但其实后来看了一些人的提交之后,发现正向的计数是可以实现的)。而之后就考虑反向的计数,发现的问题和解决方案也就如上文所述。
code
1 #include <bits/stdc++.h> 2 3 #define ll long long 4 #define INF 0x3f3f3f3f 5 using namespace std; 6 const int maxn = 3e3 + 7; 7 8 struct edge{ 9 int u, v, nxt, f; 10 }; 11 12 char ch[maxn][maxn]; 13 edge e[maxn * maxn]; 14 int head[maxn * maxn], tot, ver[maxn * maxn], nxt[maxn * maxn], wi[maxn * maxn]; 15 int dep[maxn * maxn], cur[maxn * maxn]; 16 int S, T; 17 int dc[4][2] = {{1, 0}, {0, 1}}; 18 19 20 void Init(){ 21 memset(head, -1, sizeof (head)); 22 memset(cur, 0, sizeof (cur)); 23 tot = 0; 24 } 25 26 void adde(int u, int v, int f){ 27 ver[tot] = v; wi[tot] = f; nxt[tot] = head[u]; head[u] = tot++; 28 ver[tot] = u; wi[tot] = 0; nxt[tot] = head[v]; head[v] = tot++; 29 } 30 31 bool bfs(){ 32 queue <int> q; 33 memset(dep, -1, sizeof (dep)); 34 dep[S] = 0; q.push(S); 35 36 while (!q.empty()){ 37 int h = q.front(); q.pop(); 38 39 for (int i=head[h]; ~i; i=nxt[i]){ 40 int v = ver[i]; 41 if (dep[v] == -1 && wi[i] > 0){ 42 dep[v] = dep[h] + 1; 43 q.push(v); 44 if (v == T) return true; 45 } 46 } 47 } 48 return false; 49 } 50 51 int dfs(int x, int mw){ 52 if (x == T || !mw) return mw; 53 int sum = 0; 54 for (int i=cur[x]; ~i; i = nxt[i]){ 55 cur[x] = i; 56 int v = ver[i]; 57 if (dep[v] == dep[x] + 1 && wi[i] > 0){ 58 int flow = dfs(v, min(wi[i], mw)); 59 if (flow){ 60 sum += flow; 61 mw -= flow; 62 wi[i] -= flow; 63 wi[i^1] += flow; 64 if (!mw) break; 65 } 66 } 67 } 68 if (!sum) dep[x] = -1; 69 return sum; 70 } 71 72 int dinic(){ 73 int ans = 0; 74 while(bfs()){ 75 for (int i=S; i<=T; i++) cur[i] = head[i]; 76 ans += dfs(S, INF); 77 } 78 return ans; 79 } 80 81 int main(){ 82 // cout << ('B' ^ 'W') << endl; 83 Init(); 84 85 int n; scanf("%d", &n); 86 // cout << 111 << endl; 87 for (int i=1; i<=n; i++) scanf("%s", ch[i] + 1); 88 S = 0; T = n * n + 1; 89 for (int i=1; i<=n; i++){ 90 for (int j=1; j<=n; j++){ 91 if ((i ^ j) & 1 && ch[i][j] != '?') ch[i][j] ^= ('B' ^ 'W'); 92 } 93 } 94 95 for (int i=1; i<=n; i++){ 96 for (int j=1; j<=n; j++){ 97 if (ch[i][j] == 'B') adde(S, (i-1)*n+j, INF); 98 if (ch[i][j] == 'W') adde((i-1)*n+j, T, INF); 99 for (int k=0; k<2; k++){ 100 int x = i + dc[k][0], y = j + dc[k][1]; 101 if (x < 1 || y < 1 || x > n || y > n) continue; 102 adde((i-1)*n+j, (x-1)*n+y, 1); 103 adde((x-1)*n+y, (i-1)*n+j, 1); 104 } 105 } 106 } 107 108 int ans = dinic(); 109 printf("%d\n", 2 * (n-1) * n - ans); 110 return 0; 111 }


