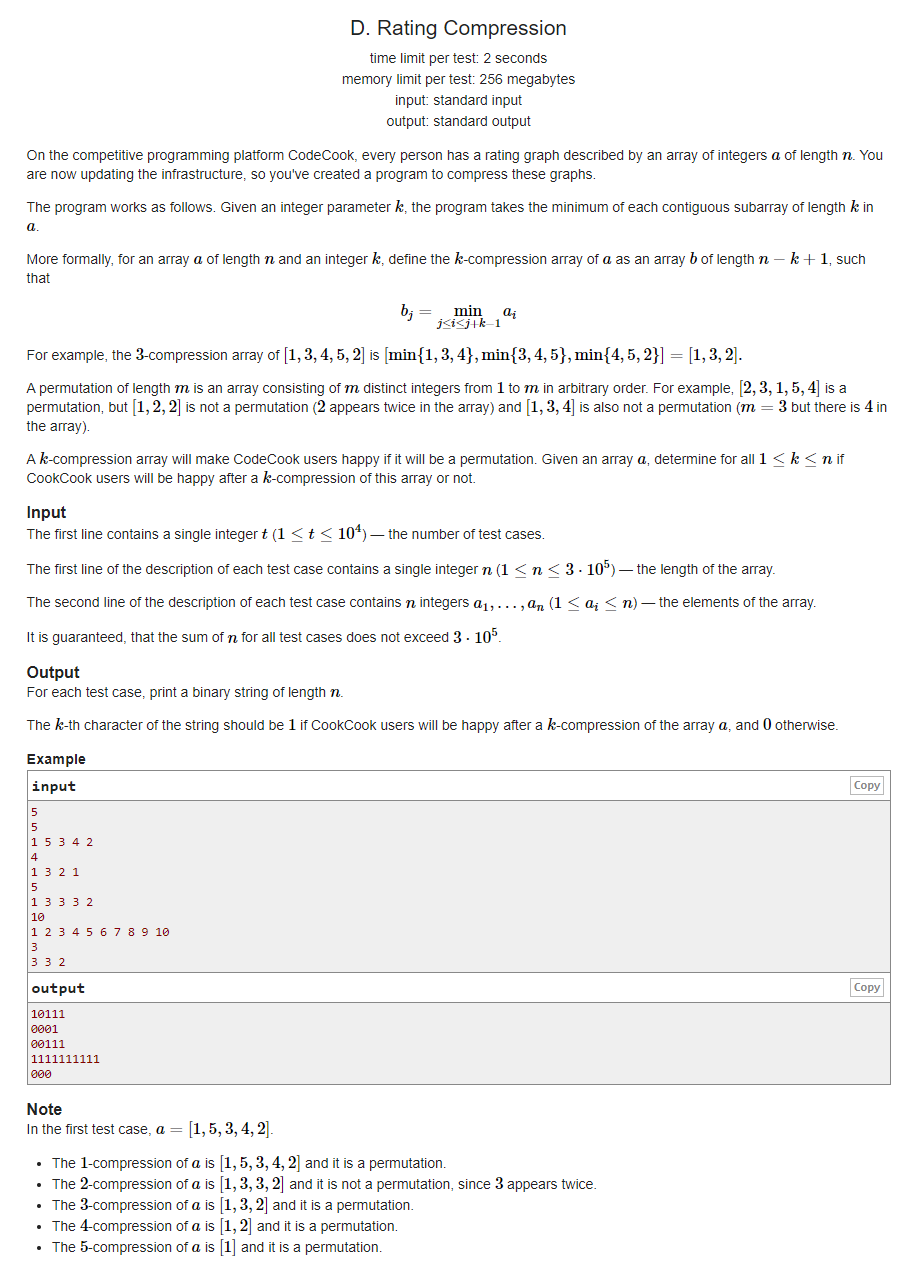
D. Rating Compression（Codeforces Global Round 12）

题目来源

https://codeforces.ml/contest/1450/problem/D

题意分析

　　给一个长度为n的数字序列。求所有长度为k的区间的最小值，是否能组合成一个从1到n-k+1的排列（置换），若能则a[k] = 1，否则为1。求a[1] - a[n]。

思路分析

　　当k=1的时候，只要原来长度为n的数字序列为一个n的排列才合法。
　　而当k>1的时候，我们可以发现，最小的数一定是在该区间的边缘。就1而言，他一定是在整个序列的最左端或者是最右端，这样才不会影响到其他区间的最小值。同样，当我们把1去掉之后，就会有下一个最小值要进行与1相同的同样的操作。
　　所以我们定义左右指针。让这两个指针从两边从中间靠拢，每一次判断[l , r]这个区间其最小值是否满足此时的最小值。若满足再进行判断其左右端点是否就是此时的最小值。当不满足的时候，其比之小的区间都是不合法的区间。
　　而还需要处理的地方就是，每一次处理区间最小值的时候，可以用各种数据结构进行处理，不然会超时（大致算一算时间复杂度？）。这里采用了线段树。

code

 

#include <bits/stdc++.h>

#define INF 0x3f3f3f3f
using namespace std;
const int maxn = 3e5 + 7;
int a[maxn], ans[maxn];
bool vis[maxn];
int tree[maxn << 2];

void build(int p, int l, int r){
    if (l == r){
        tree[p] = a[l]; return;
    }
    int mid = l + r >> 1;
    build(p << 1, l, mid);
    build(p << 1 | 1, mid + 1, r);
    tree[p] = min(tree[p << 1], tree[p << 1 | 1]);
}

int ask(int p, int l, int r, int L, int R){
    if (L <= l && r <= R) return tree[p];
    int mid = l + r >> 1;
    int ans = INF;
    if (mid >= L) ans = min(ans, ask(p << 1, l, mid, L, R));
    if (mid < R) ans = min(ans, ask(p << 1 | 1, mid + 1, r, L, R));
    return ans;
}

int main(){
    int t; scanf("%d", &t);
    while (t --){
        int n; scanf("%d", &n);
        int mmin = INF;
        for (int i=1; i<=n; i++) vis[i] = false;
        for (int i=1; i<=n; i++){
            scanf("%d", &a[i]);
            mmin = min(mmin, a[i]);
            vis[a[i]] = true;
        }
        build(1, 1, n);
        int cnt = 0;
        for (int i=1; i<=n; i++){
            if (vis[i]) cnt = i;
            else break;
        }
        if (cnt == n) ans[1] = 1;
        else ans[1] = 0;
        if (mmin == 1) ans[n] = 1;
        int l = 1, r = n, p = 0;
        while (l <= r){
            p ++;
            int mmin = ask(1, 1, n, l, r);
            if (mmin == p){
                ans[r - l + 1] = 1;
                if (a[l] == p){
                    l ++; continue;
                }
                if (a[r] == p){
                    r --; continue;
                }
                for (int i=2; i<=r-l; i++) ans[i] = 0;
                break;
            }
//            ans[r - l + 1] = 1;
            for (int i=2; i<=r-l+1; i++) ans[i] = 0;
            break;
        }
//        cout << "!!!  ";
        for (int i=1; i<=n; i++) printf("%d", ans[i]);
        printf("\n");
    }
    return 0;
}